Understanding the shape of data distributions is a fundamental concept in statistics and data analysis. By examining the shape of a data distribution, we can gain insights into the underlying patterns and characteristics of the data. In Lesson 4, we explore the different shapes that data distributions can take and discuss what they reveal about the data.
One important aspect of data distributions is their symmetry or skewness. A symmetric distribution is one where the data values are evenly distributed around the mean, resulting in a bell-shaped curve. On the other hand, a skewed distribution is one where the data values are concentrated more to one side of the mean, leading to a tail on one side of the curve. Understanding the symmetry or skewness of a data distribution is essential for making accurate interpretations and predictions.
Another aspect of data distributions is the presence of outliers. An outlier is a data point that significantly deviates from the overall pattern of the data. Outliers can have a significant impact on the shape of a data distribution, causing it to be skewed or distorted. Identifying and properly handling outliers is crucial to ensure the accuracy and reliability of any statistical analysis or data modeling.
In Lesson 4, we also delve into the concept of measures of central tendency, such as the mean, median, and mode. These measures provide information about the center or average value of a data distribution. Understanding how these measures relate to the shape of the data distribution allows us to better interpret and analyze the data accurately.
Lesson 4 Shape of Data Distributions Answers
In Lesson 4, we explored the different shapes that data distributions can take. We learned that data can have a symmetrical distribution, where the values are evenly spread around the mean. This is often referred to as a bell-shaped curve or a normal distribution.
On the other hand, data can also have a skewed distribution, where the values are concentrated more towards one end of the distribution. There are two types of skewness: positive skewness, where the tail of the distribution is towards the right, and negative skewness, where the tail is towards the left.
- When data has a symmetrical distribution, the mean, median, and mode are all the same value. This is because the data is evenly spread around the center.
- In a positively skewed distribution, the mean is greater than the median, as the tail pulls the mean towards the higher values.
- In a negatively skewed distribution, the mean is less than the median, as the tail pulls the mean towards the lower values.
Understanding the shape of a data distribution is important in data analysis. It helps us determine the appropriate statistical measures to use, and it gives us insights into the characteristics of the data. By examining the shape of the data, we can make more informed decisions and draw meaningful conclusions.
What is Data Distribution?
Data distribution refers to the way data is spread or distributed across different values or categories in a dataset. It provides information about the frequency or occurrence of different values or categories in the dataset. Understanding data distribution is essential for analyzing, summarizing, and making inferences from data.
Data can be distributed in various ways, and the shape of the distribution provides insights into the underlying patterns or characteristics of the data. Common types of data distributions include normal distributions, skewed distributions, bimodal distributions, and uniform distributions.
- A normal distribution, also known as a bell curve, is symmetric around the mean. The majority of the data is concentrated around the mean, with decreasing frequency as we move further away from the mean.
- A skewed distribution occurs when the data is not evenly distributed around the mean. It can be positively skewed (skewed to the right) or negatively skewed (skewed to the left).
- A bimodal distribution has two distinct peaks, indicating that the data is derived from two separate populations or processes.
- A uniform distribution occurs when all values or categories have equal frequency or probability of occurrence.
Analyzing the data distribution helps in understanding central tendency (mean, median, mode), variability (range, standard deviation), and identifying outliers. It also aids in selecting appropriate statistical tests and making accurate predictions or decisions based on the data. Data visualization techniques, such as histograms, box plots, and scatter plots, are commonly used to visually represent and explore data distributions.
Types of Data Distributions
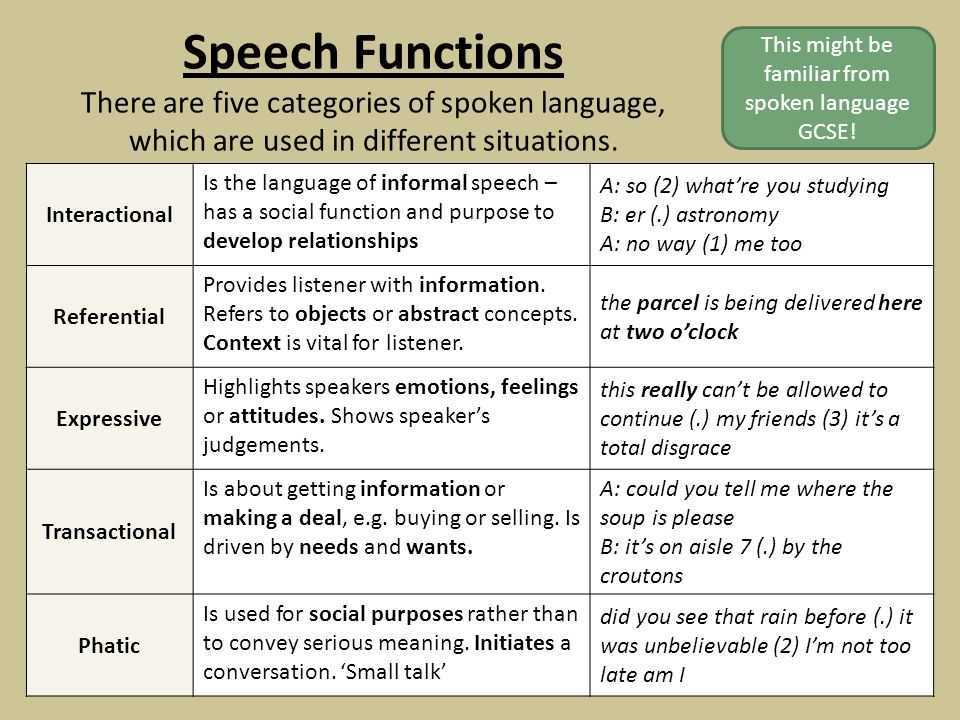
Data distributions refer to how data is spread across different values. Understanding the types of data distributions is essential for data analysis and interpretation. There are several common types of data distributions, including:
- Uniform Distribution: In a uniform distribution, all values have an equal chance of occurring. This type of distribution forms a flat line on a histogram.
- Symmetric Distribution: A symmetric distribution is characterized by having values that are evenly distributed around a central point. The most common example of a symmetric distribution is the normal distribution.
- Skewed Distribution: Skewed distributions are asymmetrical, with the tail of the distribution stretching towards either the left or right side. When the tail extends to the right, it is called a right-skewed distribution, while a left-skewed distribution has its tail extending to the left.
- Multimodal Distribution: When a data set has more than one distinct peak or mode, it is said to have a multimodal distribution. This can occur when there are different groups or clusters within the data.
- Exponential Distribution: An exponential distribution is characterized by a constant rate of decay. It is often used to model events that occur randomly over time.
Understanding the type of data distribution is important because it can help determine the appropriate statistical analysis techniques and inferential methods to use. It provides insights into the characteristics and patterns of the data, allowing for accurate interpretation and decision-making.
Normal Distribution
The normal distribution, also known as the Gaussian distribution, is one of the most important probability distributions in statistics. It is a continuous probability distribution defined by a symmetric bell-shaped curve. The shape of the curve is determined by two parameters: the mean (µ) and the standard deviation (σ). The mean represents the center of the distribution, while the standard deviation measures the average amount of variation or dispersion around the mean.
The normal distribution is characterized by several properties. First, it is symmetric around the mean, with the highest point of the curve located at the mean value. Second, it is asymptotic, meaning that the tails of the curve extend indefinitely and never touch the x-axis. Third, the total area under the curve is equal to 1, representing the probability of observing any value within the distribution.
The normal distribution is widely used in various fields, including statistics, finance, and natural sciences, due to its mathematical properties and applicability to real-world phenomena. It provides a convenient and powerful tool for modeling and analyzing data, as many real-world phenomena approximate a normal distribution. Furthermore, many statistical techniques and tests are based on the assumption of normality, making it an essential concept in statistical inference.
Skewed Distributions
In statistics, a skewed distribution refers to the shape of a data set that is not symmetrical. It means that the data is skewed to one side or the other, rather than being evenly distributed around the mean. This can be visualized by looking at a histogram or a box plot of the data.
There are two main types of skewed distributions: positively skewed and negatively skewed. In a positively skewed distribution, the tail of the data is longer on the right side, and the majority of the data is concentrated on the left side. This means that there are fewer extreme values on the right side of the distribution. On the other hand, in a negatively skewed distribution, the tail of the data is longer on the left side, and the majority of the data is concentrated on the right side. This means that there are fewer extreme values on the left side of the distribution.
A positively skewed distribution is also known as a right-skewed distribution, while a negatively skewed distribution is known as a left-skewed distribution. The direction of the skewness is named after the longer tail of the data. Skewness is a measure of the asymmetry of a distribution and can be calculated using statistical formulas. Understanding the skewness of a distribution can provide important insights about the data and help to make more accurate interpretations and predictions.
Symmetric Vs. Asymmetric Distributions
A distribution refers to the arrangement or spread of data values. It helps us understand the overall pattern of a dataset. One important characteristic of a distribution is its symmetry or asymmetry. A symmetric distribution is one in which the data is evenly distributed around a central point. On the other hand, an asymmetric distribution, also known as a skewed distribution, is one in which the data is not evenly distributed around a central point and is skewed to one side.
In a symmetric distribution, the mean, median, and mode are all located at the same point, known as the center of the distribution. This means that there are equal numbers of data points on either side of the center. The shape of a symmetric distribution is usually bell-shaped, with the highest frequency occurring at the center and gradually decreasing towards the tails.
In contrast, an asymmetric distribution can be either positively skewed or negatively skewed. In a positively skewed distribution, the tail of the distribution extends towards the right side, while in a negatively skewed distribution, the tail extends towards the left side. The mean is generally pulled in the direction of the tail, while the median remains closer to the center of the distribution. The mode may or may not be affected by the skewness.
Understanding the symmetry or asymmetry of a distribution is important in data analysis as it provides insights into the underlying patterns and characteristics of the dataset. It helps in determining the appropriate statistical measures to use and in making valid interpretations of the data.
Bimodal Distributions
Bimodal distributions, as the name suggests, are distributions that have two distinct peaks or modes. These types of distributions are characterized by having two separate clusters of data points, each centered around a different value. Bimodal distributions can arise in various scenarios and can provide valuable insights into the underlying data.
One common example of a bimodal distribution is when analyzing the heights of individuals in a population. In such cases, there may be two distinct clusters of heights, one corresponding to males and another to females. This leads to the bimodal distribution as the two clusters have different average heights. By identifying and understanding this bimodal distribution, researchers can gain insights into the characteristics of the population being studied.
Another example of a bimodal distribution can be observed in the distribution of test scores in a classroom. If the test is relatively easy for some students, they may score very high, resulting in a peak at the high end of the distribution. On the other hand, if the test is challenging for some students, they may score very low, resulting in a peak at the low end of the distribution. This bimodal distribution can indicate the presence of two distinct groups of students – those who performed well and those who didn’t perform well on the test.
In conclusion, bimodal distributions are characterized by having two distinct peaks or modes, indicating the presence of two separate clusters of data points. These distributions can provide valuable insights into the underlying data and can be observed in various scenarios, such as analyzing heights in a population or test scores in a classroom.
Measures of Central Tendency for Data Distributions
The measures of central tendency are statistical calculations that represent the average, typical, or center value of a data distribution. They help summarize and describe the overall characteristics of the data set. The three main measures of central tendency are the mean, median, and mode.
The mean, or average, is calculated by summing up all the values in the data set and dividing the sum by the total number of values. It is highly influenced by extreme values, called outliers. The median represents the middle value when the data set is sorted in ascending or descending order. It is less affected by outliers and provides a better representation of the typical value in the data set. The mode is the value or values that occur most frequently in the data set. It may not always exist or may have multiple modes.
- Mean: The mean is commonly used to represent the average value of a data set. It is calculated by summing up all the values and dividing by the total number of values. It is sensitive to outliers, as extreme values can greatly influence its calculation.
- Median: The median is the middle value in a data set when arranged in ascending or descending order. It divides the data set into two equal halves. It is less affected by outliers and provides a better representation of the central tendency.
- Mode: The mode is the value that appears most frequently in a data set. It may not always exist or may have multiple modes. It is useful for identifying the most common observation or category in the data set.