
In Lesson 6 1 of the mathematics curriculum, students are introduced to the concept of identifying and representing functions. Functions are a fundamental concept in mathematics and are widely used in various fields. The ability to identify and represent functions is essential for solving problems and analyzing data in real-world situations.
The lesson begins by introducing the definition of a function as a relationship between two sets of numbers, where each input has exactly one corresponding output. Students learn how to determine whether a relationship is a function by analyzing the given set of ordered pairs or a graph.
Through various examples and exercises, students practice identifying functions using different representations, such as tables, graphs, and equations. They learn to recognize patterns and understand how changes in one set of numbers affect the other set. The lesson also covers the concept of domain and range, which are the sets of all possible inputs and outputs of a function, respectively.
By the end of the lesson, students are equipped with the skills to identify and represent functions in different formats and understand the significance of functions in problem-solving and data analysis. This foundational knowledge sets the stage for further exploration of more complex functions and their applications in higher-level mathematics and other disciplines.
Lesson 6: Identifying and Representing Functions Answer Key
In Lesson 6, we will be discussing how to identify and represent functions. A function is a relationship between two sets of numbers, known as the input and output sets. The input set consists of all possible values of the independent variable, while the output set consists of all possible values of the dependent variable.
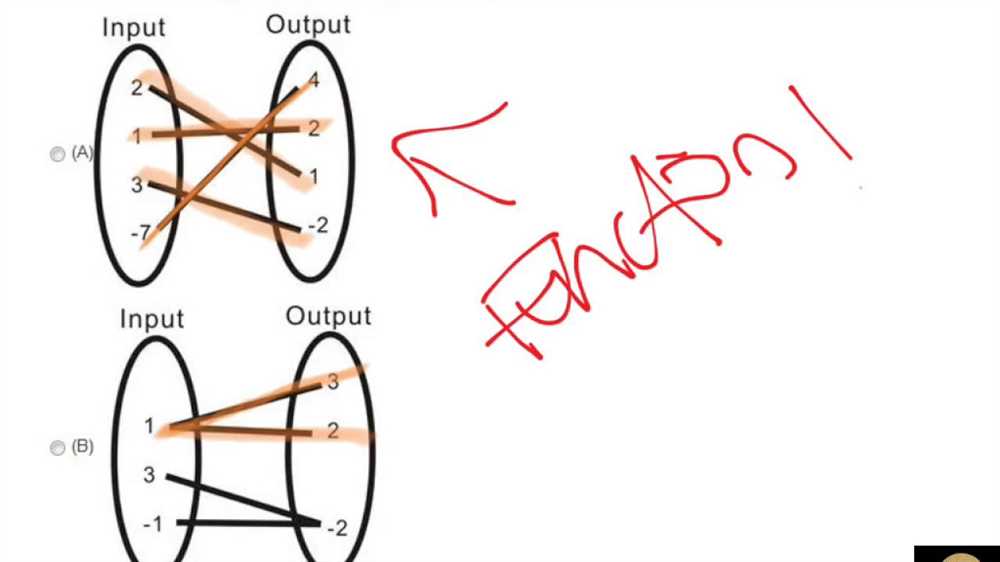
To identify a function, we need to determine if each input value corresponds to exactly one output value. This can be done by examining a set of ordered pairs or by using the vertical line test. If a vertical line intersects the graph of the relation at more than one point, then it is not a function.
The answer key for Lesson 6 provides solutions to the exercises and practice problems that focus on identifying and representing functions. It includes step-by-step explanations and examples to help students understand the concepts and apply them correctly. The answer key also provides additional practice problems for students to reinforce their understanding of the material.
By using the answer key, students can check their work and compare their solutions to the correct answers. This allows them to identify any mistakes or misunderstandings they may have and seek clarification or further assistance if needed. The answer key serves as a valuable tool for both students and teachers to assess learning and progress in the topic of identifying and representing functions.
In conclusion, Lesson 6: Identifying and Representing Functions Answer Key is a helpful resource for students to practice and refine their skills in identifying and representing functions. It provides detailed explanations and examples, allowing students to develop a solid understanding of the topic. By using the answer key, students can self-assess and seek further assistance if needed, leading to improved learning outcomes.
What are Functions?
A function is a mathematical concept that relates inputs to outputs. It represents a relationship between two sets, where each element of the first set (the domain) is associated with exactly one element of the second set (the range). Functions can be represented in various ways, such as through equations, tables, graphs, or verbal descriptions.
In mathematical language, a function can be defined as a rule that assigns each input value from the domain to a unique output value from the range. This rule can be expressed using notation such as f(x) or y = f(x), where x is the input and f(x) (or y) is the corresponding output. The input values are often referred to as independent variables, while the output values are called dependent variables.
Functions can be classified based on their behavior:
- A linear function has a constant rate of change and can be represented by a straight line on a graph.
- An exponential function grows or decays exponentially and can be represented by a curve that gets steeper or flatter.
- A quadratic function has a parabolic shape and can be represented by a U-shaped graph.
- A trigonometric function relates angles to ratios of side lengths in a right triangle and can be represented by a wave-like graph.
Functions are widely used in various fields, such as physics, engineering, economics, and computer science, to model and analyze relationships between variables. They provide a framework for understanding and predicting how one set of values influences another set of values, making them an essential tool in problem-solving and decision-making processes.
Identifying Functions

A function is a relationship between two sets of numbers, where each input value (x) has exactly one corresponding output value (y). It can be represented as an equation, a table, or a graph. Being able to identify functions is an important skill as it allows us to understand and analyze various mathematical and real-world scenarios.
One way to identify a function is by looking at a set of ordered pairs or a table. If each input value is paired with only one output value, then it is a function. For example, in the table:
| x | y |
|---|---|
| 1 | 5 |
| 2 | 7 |
| 3 | 9 |
Each input value (x) is associated with only one output value (y), so this table represents a function.
Another way to determine if a relationship is a function is by examining a graph. If each vertical line intersects the graph at most once, then it is a function. This is called the vertical line test. For example, in the graph below:

Each vertical line intersects the graph at most once, so this graph represents a function.
In summary, identifying functions involves looking for a one-to-one correspondence between input and output values. Whether it is through equations, tables, or graphs, understanding functions helps us analyze and solve various mathematical problems.
Notation for Functions
In mathematics, a function is a relationship between a set of inputs and a set of outputs, where each input is associated with exactly one output. Functions are commonly written using a notation that consists of various symbols and expressions, which help to represent and describe their properties.
One common way to represent functions is using function notation. Function notation typically involves using the letter “f” followed by parentheses, with the input variable placed inside the parentheses. For example, if we have a function that takes the input variable “x” and produces the output variable “y”, we can write it as f(x) = y. This notation helps to indicate that “f” is the name of the function, “x” is the input variable, and “y” is the output variable that is produced when the function is applied to the input.
Another commonly used notation for functions is the mapping notation. In mapping notation, a function is represented as a set of ordered pairs, where the first element of each pair represents the input and the second element represents the output. For example, if we have a function that maps the input value of 2 to the output value of 4, and the input value of 3 to the output value of 6, we can write it as {(2, 4), (3, 6)}. This notation helps to show the specific input-output pairs that are associated with the function.
Overall, the notation used for functions serves as an important tool for representing and describing the relationship between inputs and outputs in mathematics. Whether using function notation or mapping notation, these symbols and expressions help to provide a clear and concise representation of how a function operates.
Representing Functions in Tables
Tables are a useful tool for representing functions. They provide a clear and organized way to display the relationship between the input and output values of a function. In a function table, the input values are typically listed in one column, while the corresponding output values are listed in another column.
Each row in the table represents a different input value, and the corresponding output value is determined by the function rule. For example, if the function rule is to double the input value, then each output value in the table would be twice the corresponding input value. This allows us to easily see how the function behaves for different inputs.
A function table can be used to quickly evaluate and graph a function. By plugging different input values into the function rule and listing the corresponding output values in the table, we can create a visual representation of how the function behaves. This can be especially helpful when trying to understand the overall pattern or trend of a function.
Furthermore, a function table can be used to find specific output values for given input values, or to find the input value for a given output value. By looking up the desired input or output value in the table, we can easily find the corresponding value from the other column. This makes it easier to work with functions and perform calculations.
In conclusion, representing functions in tables provides a visual and organized way to display the relationship between input and output values. Whether it’s for evaluating, graphing, or finding specific values, a function table is a valuable tool for working with functions.
Representing Functions on Graphs
When discussing functions, it is important to be able to represent them graphically. Graphs allow us to visualize the relationship between inputs and outputs in a function, making it easier to analyze and understand the behavior of the function.
To represent a function on a graph, we typically use a coordinate plane with the input values, or domain, on the x-axis and the output values, or range, on the y-axis. Each point on the graph corresponds to an input-output pair in the function.
One way to represent functions on graphs is through a scatter plot. In a scatter plot, we simply plot each input-output pair as an individual point on the graph. This can be useful for visualizing the data points in the function and identifying any patterns or trends.
Another way to represent functions on graphs is through a line or curve. When the input-output pairs in a function follow a specific pattern or trend, we can represent this relationship by drawing a line or curve that best fits the points on the graph. This can help us understand the overall behavior of the function and make predictions about other input-output pairs.
It is important to note that not all graphs represent functions. In order for a graph to represent a function, each input value must have only one corresponding output value. This means that the graph should pass the vertical line test, where no vertical line intersects the graph more than once.
In summary, representing functions on graphs allows us to visualize and analyze their behavior. We can use scatter plots to show the individual input-output pairs, or draw lines or curves to represent patterns or trends in the function. It is important to ensure that the graph passes the vertical line test to confirm that it represents a function.
Evaluating Functions

When working with functions, one common task is to evaluate them for specific input values. Evaluating a function means finding the output value of the function for a given input. It allows us to understand how the function behaves and how it relates to the input values.
To evaluate a function, we replace the independent variable in the function expression with the given input value and simplify the expression. The result is the corresponding output value of the function.
For example, let’s consider the function f(x) = 2x + 3. If we want to evaluate this function for the input value x = 4, we replace x with 4 in the expression: f(4) = 2(4) + 3. Simplifying this expression gives us f(4) = 8 + 3 = 11. Therefore, when the input is 4, the output of the function f is 11.
Evaluating functions is an essential skill in mathematics, as it helps us analyze and interpret the behavior of functions in different contexts. It allows us to make predictions, solve equations, and understand the relationship between variables and their corresponding values.
In summary, evaluating a function involves replacing the independent variable with a given input value and simplifying the expression to find the corresponding output value. This process helps us understand how the function behaves and its relationship with the input values.
Domain and Range
The concept of domain and range is fundamental in understanding functions. The domain of a function refers to the set of all possible input values or x-values for which the function is defined. It represents the values that you can plug into the function to obtain an output. The range, on the other hand, is the set of all possible output values or y-values that the function can produce. It represents the values that the function can take on.
In mathematical terms, the domain and range of a function can be represented using set notation. The domain is usually denoted as D or Dom(f), while the range is denoted as R or Ran(f). For example, if we have a function f(x) = x^2, the domain would be all real numbers, denoted as D = (-∞, ∞), since any real number can be squared. The range, however, would be all non-negative real numbers, denoted as R = [0, ∞), since squaring a number always yields a non-negative result.
When identifying the domain and range of a function, it’s important to consider any restrictions or limitations on the variable. For instance, if we have a function that represents the height of a tree, it would not make sense to have negative values for the height. Therefore, the domain would be restricted to positive numbers only. Additionally, the range would also be limited by factors such as the maximum possible height of a tree.
In summary, the domain of a function represents the set of all possible input values, while the range represents the set of all possible output values. Understanding the domain and range is crucial for properly defining and analyzing functions.