
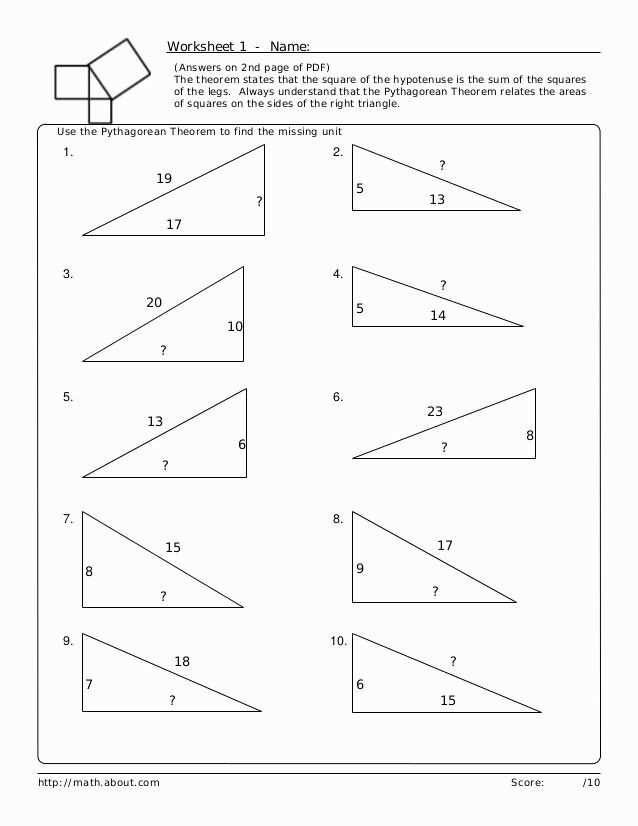
In Lesson 6, we learned about the Pythagorean theorem and how to use it to calculate the length of the sides of a right triangle. This theorem is a fundamental concept in geometry and is widely used in various applications, such as construction, navigation, and engineering. In this homework practice, we will apply the Pythagorean theorem to solve real-world problems and strengthen our understanding of the concept.
To start, we will review the Pythagorean theorem, which states that in a right triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. This can be written as a formula: a² + b² = c², where a and b are the lengths of the two legs and c is the length of the hypotenuse.
Using this formula, we can solve problems involving right triangles and find missing side lengths. We will be given information about the lengths of two sides and we need to find the length of the third side. By substituting the given values into the Pythagorean theorem equation and solving for the missing side length, we can successfully complete the homework assignments.
This homework practice will not only strengthen our understanding of the Pythagorean theorem but also enhance our problem-solving skills and ability to apply mathematical concepts to real-life situations. By practicing these problems, we will become more confident in our knowledge and be prepared for future lessons and assessments on this topic.
Lesson 6 Homework Practice: Use the Pythagorean Theorem Answer Key

In this lesson, we will explore the Pythagorean Theorem and how it can be used to solve for the missing side lengths of right triangles. The Pythagorean Theorem states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides.
To solve for the missing side lengths, we can use the Pythagorean Theorem formula:
c² = a² + b²
Where c represents the length of the hypotenuse, and a and b represent the lengths of the other two sides. We can plug in the known values and solve for the missing side length.
For example, if we have a right triangle with a hypotenuse of length 5 and one side of length 3, we can plug those values into the formula:
c² = a² + b²
5² = 3² + b²
25 = 9 + b²
b² = 16
b = 4
So, the missing side length is 4.
Using the Pythagorean Theorem, we can solve for missing side lengths in any right triangle. It is a powerful tool that allows us to find the length of sides without having to measure them directly. This theorem is especially useful in real-world applications, such as construction, engineering, and navigation.
What is the Pythagorean Theorem?
The Pythagorean Theorem is a fundamental concept in mathematics that relates to the relationships between the sides of a right triangle. It is named after the ancient Greek mathematician Pythagoras, who is credited with discovering this important mathematical relationship.
The Pythagorean Theorem states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. This can be written as the equation “a^2 + b^2 = c^2”, where “a” and “b” represent the lengths of the two legs of the triangle and “c” represents the length of the hypotenuse.
The Pythagorean Theorem is not only a theoretical concept, but it also has practical applications in various fields, such as architecture, engineering, and physics. It allows us to calculate the length of one side of a triangle if we know the lengths of the other two sides. This theorem forms the basis for trigonometry and is an essential tool in solving problems involving right triangles.
Example:
Let’s say we have a right triangle with one side measuring 5 units and another side measuring 12 units. To find the length of the hypotenuse, we can use the Pythagorean Theorem. By substituting the values into the equation “a^2 + b^2 = c^2”, we get “5^2 + 12^2 = c^2”. Simplifying, we have “25 + 144 = c^2”. Adding these values together, we get “169 = c^2”. Taking the square root of both sides, we find that the length of the hypotenuse is approximately 13 units.
In conclusion, the Pythagorean Theorem is a powerful mathematical tool that allows us to find the relationships between the sides of a right triangle. It has numerous applications in real-world scenarios and is an essential concept in mathematics.
Understanding the Formula of the Pythagorean Theorem

The Pythagorean Theorem is a fundamental concept in mathematics that relates to the relationship between the sides of a right triangle. It states that the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.
This theorem can be expressed using the formula: c^2 = a^2 + b^2, where c represents the hypotenuse and a and b represent the other two sides of the triangle.
To understand the formula, it is important to visualize how it applies to a right triangle. Imagine a right triangle where side a is the base and side b is the height. The hypotenuse, side c, is the longest side and forms the diagonal across the triangle. The formula shows that the square of the hypotenuse’s length is equal to the sum of the squares of the lengths of the other two sides.
The Pythagorean Theorem is useful for solving various types of problems involving right triangles, such as finding missing side lengths or determining whether a triangle is a right triangle. It provides a mathematical basis for understanding the relationships between the sides of a right triangle and is a key concept in trigonometry and geometry.
Summary:

- The Pythagorean Theorem relates to the relationship between the sides of a right triangle.
- The formula is c^2 = a^2 + b^2, where c is the hypotenuse and a and b are the other two sides.
- Visualizing the formula helps understand its application to right triangles.
- The theorem is useful in solving problems involving right triangles.
- It provides a basis for understanding relationships in trigonometry and geometry.
Applying the Pythagorean Theorem in Real-World Scenarios
The Pythagorean theorem is a fundamental concept in mathematics that allows us to calculate the length of one side of a right triangle when the lengths of the other two sides are known. But how can we use this theorem in real-world scenarios? Let’s explore a few examples.
Example 1: Determining the distance between two points
Say you have two points on a coordinate plane, A(x1, y1) and B(x2, y2). You can use the Pythagorean theorem to find the distance between these two points. By treating the line connecting the two points as the hypotenuse of a right triangle, you can calculate the length of this line using the theorem.
Example 2: Calculating the height of a building
If you want to determine the height of a building and you have access to a tape measure, you can use the Pythagorean theorem to do so. Stand a certain distance away from the base of the building, measure the angle of elevation to the top of the building, and measure the distance from your position to the base of the building. Using these measurements, along with the theorem, you can calculate the height of the building.
Example 3: Finding the length of a diagonal
Suppose you have a rectangular prism and you want to find the length of the diagonal connecting two opposite corners of the prism. By considering the three sides of the prism as the three sides of a right triangle, you can use the Pythagorean theorem to determine the length of the diagonal.
These are just a few examples of how the Pythagorean theorem can be applied to real-world scenarios. Whether it’s measuring distances, calculating heights, or finding diagonals, this theorem allows us to solve practical problems using mathematical principles.
Step-by-Step Problem Solving Using the Pythagorean Theorem
The Pythagorean Theorem is a fundamental concept in geometry that allows us to find the length of one side of a right triangle if we know the lengths of the other two sides. This theorem is named after the ancient Greek mathematician Pythagoras, who discovered it around 500 BCE.
To solve a problem using the Pythagorean Theorem, we need to follow a systematic approach. Here is a step-by-step guide:
- Identify the right angle: Look for the angle that measures 90 degrees in the triangle. This angle is located opposite the longest side, known as the hypotenuse.
- Label the sides: Assign labels to the three sides of the right triangle. The side opposite the right angle is usually labeled as the hypotenuse (C), while the other two sides are referred to as the legs (A and B).
- Apply the Pythagorean Theorem: The Pythagorean Theorem states that the square of the hypotenuse is equal to the sum of the squares of the two legs. In mathematical terms, this can be written as: C^2 = A^2 + B^2.
- Substitute the values: Plug in the given lengths of the legs (A and B) into the equation. Solve for the hypotenuse (C) by taking the square root of both sides of the equation.
- Check your answer: Verify that your solution makes sense. Check if the lengths of the sides satisfy the conditions of a right triangle. Also, double-check your calculations to ensure accuracy.
By following these steps, you can confidently solve problems involving the Pythagorean Theorem and find the missing side lengths of right triangles. Remember to practice regularly to strengthen your problem-solving skills!
Common Mistakes to Avoid when Using the Pythagorean Theorem
The Pythagorean Theorem is a fundamental concept in geometry that helps us find the length of the hypotenuse or one of the legs of a right triangle. However, there are some common mistakes that people make when using this theorem. By being aware of these mistakes, you can ensure accurate calculations and avoid any errors.
1. Forgetting to square the lengths of the legs: One of the most common mistakes is not squaring the lengths of the legs of the right triangle. The theorem states that the square of the hypotenuse is equal to the sum of the squares of the lengths of the legs. It is important to square both the length of the base and the length of the height of the triangle before adding them together.
2. Using the wrong sides when applying the theorem: Another common mistake is using the wrong sides of the triangle when applying the Pythagorean Theorem. The longer side, or the hypotenuse, should always be on the same side as the right angle. Double-check that you are using the correct sides before plugging in the values into the equation.
3. Rounding off intermediate calculations: When solving problems using the Pythagorean Theorem, it’s important to keep the intermediate calculations as precise as possible. Rounding off numbers too early in the calculation can introduce errors into the final result. It’s best to carry out the calculations to several decimal places and then round off the final answer to the appropriate level of precision.
4. Assuming the triangle is a right triangle: Lastly, it’s crucial to make sure that the triangle you are working with is actually a right triangle. The Pythagorean Theorem only applies to right triangles, which have one angle measuring 90 degrees. If the triangle is not a right triangle, the theorem cannot be used to find the length of the sides.
By avoiding these common mistakes, you can confidently apply the Pythagorean Theorem to find the missing lengths in right triangles and solve geometry problems accurately.
Tips and Tricks for Using the Pythagorean Theorem Effectively
While the Pythagorean theorem is a simple concept to understand, applying it effectively in real-world problems can sometimes be challenging. To help you use the Pythagorean theorem more efficiently, here are some tips and tricks:
1. Identify the right triangle:
Before applying the Pythagorean theorem, make sure you have identified the right triangle in the problem. A right triangle is a triangle with one angle measuring 90 degrees. Remember that the Pythagorean theorem only applies to right triangles, so it’s crucial to check for the presence of a right angle.
2. Label the sides correctly:
When using the Pythagorean theorem, it’s essential to label the sides of the right triangle correctly. The longest side, opposite the right angle, is called the hypotenuse. The other two sides are referred to as the legs. Labeling the sides correctly will help you set up the equation correctly and avoid confusion.
3. Square the lengths:
To use the Pythagorean theorem, you need to square the lengths of the legs of the right triangle. This step is crucial because the Pythagorean theorem states that the sum of the squares of the lengths of the legs is equal to the square of the length of the hypotenuse. Double-check your calculations to ensure you have correctly squared the lengths before proceeding.
4. Simplify, if possible:
After squaring the lengths of the legs, you may end up with a complex equation. To simplify the equation, combine like terms and look for opportunities to cancel out common factors. Simplifying the equation will make it easier to solve and find the unknown value or verify the relationship between the sides of the right triangle.
5. Round the answer, if necessary:
Depending on the problem, you may need to round the answer to a specific decimal place or a whole number. Be aware of the given precision or the required level of accuracy and adjust your result accordingly. Rounding the answer will make it more practical and applicable to real-world scenarios.
- Summary:
Using the Pythagorean theorem effectively involves identifying the right triangle, labeling the sides correctly, squaring the lengths, simplifying the equation, and rounding the answer if needed. By following these tips and tricks, you can confidently apply the Pythagorean theorem in various problem-solving situations and achieve accurate results.