
Are you struggling with your linear relationships homework? Do you need help understanding the concepts and finding the correct answers? Look no further! In this article, we will provide you with the answer key to Linear Relationships Homework 1, along with explanations of how to solve each problem.
Linear relationships are an essential topic in mathematics, and understanding them is crucial for solving real-world problems and analyzing data. Homework assignments are designed to reinforce your understanding of these relationships and allow you to practice applying the concepts learned in class.
In this answer key, we will walk you through each question in Homework 1 and provide step-by-step solutions. Whether you are struggling with finding the equation of a line, determining slope and y-intercept, or graphing a linear equation, we’ve got you covered!
Linear Relationships Homework 1 Answer Key
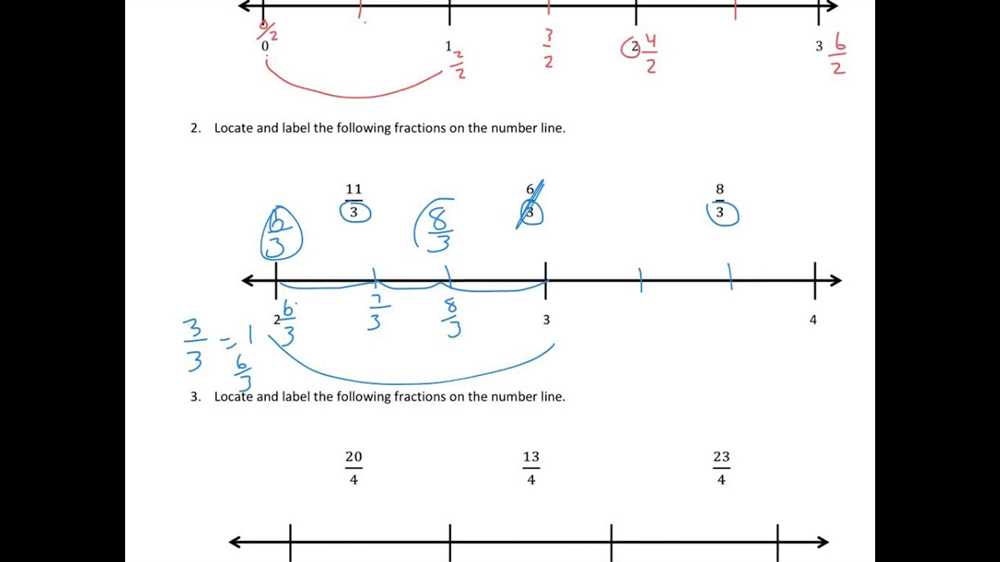
In this answer key, we will go through the solutions to the first homework assignment on linear relationships. This assignment focused on identifying and graphing linear equations, finding the slope and y-intercept, and solving equations using the slope-intercept form. Let’s dive into the answers!
Question 1:
Given the equation y = 2x + 3, we need to determine the slope and y-intercept. The slope is the coefficient of x, which in this case is 2. Therefore, the slope is 2. The y-intercept is the constant term, which in this case is 3. Therefore, the y-intercept is 3.
Question 2:
For the equation y = -0.5x + 4, we need to find the slope and y-intercept. The slope is the coefficient of x, which is -0.5. So, the slope is -0.5. The y-intercept is the constant term, which is 4. So, the y-intercept is 4.
Question 3:
The equation y = 3x – 2 represents a line with a slope of 3 and a y-intercept of -2. To graph this equation, we can start by plotting the y-intercept at the point (0, -2), and then use the slope to find additional points. The slope of 3 means that for every increase of 1 in x, the y-value will increase by 3. We can use this information to find points like (1, 1), (2, 4), and (3, 7) and connect them to graph the line.
Question 4:
To solve the equation 2x + 5 = 15, we need to isolate the variable x. We can start by subtracting 5 from both sides of the equation to get 2x = 10. Then, we divide both sides by 2 to solve for x. Therefore, the solution is x = 5.
Question 5:
For the equation y = -2x + 8, we need to find the x and y values when y is equal to 0. To do this, we can substitute 0 for y in the equation and solve for x. So, we have 0 = -2x + 8. To isolate x, we need to subtract 8 from both sides of the equation. This gives us -8 = -2x. Finally, divide both sides by -2 to solve for x. The solution is x = 4.
Question 6:
Given the equation y = 4x, we need to find the equation of the line parallel to this line and passing through the point (2, 5). To find the equation, we start with the slope of the given line, which is 4. Since the line we are looking for is parallel, it will also have a slope of 4. We can then use the point-slope form of a linear equation to find the equation. Plugging in the values, we have y – 5 = 4(x – 2). Simplifying this equation gives us y – 5 = 4x – 8. Adding 5 to both sides, we get y = 4x – 3. Therefore, the equation of the line parallel to y = 4x and passing through the point (2, 5) is y = 4x – 3.
These are the solutions to the first homework assignment on linear relationships. By understanding the concepts of slope, y-intercept, and the forms of linear equations, you can solve problems involving graphing and equations easily. Keep practicing to strengthen your skills!
Definition of a Linear Relationship
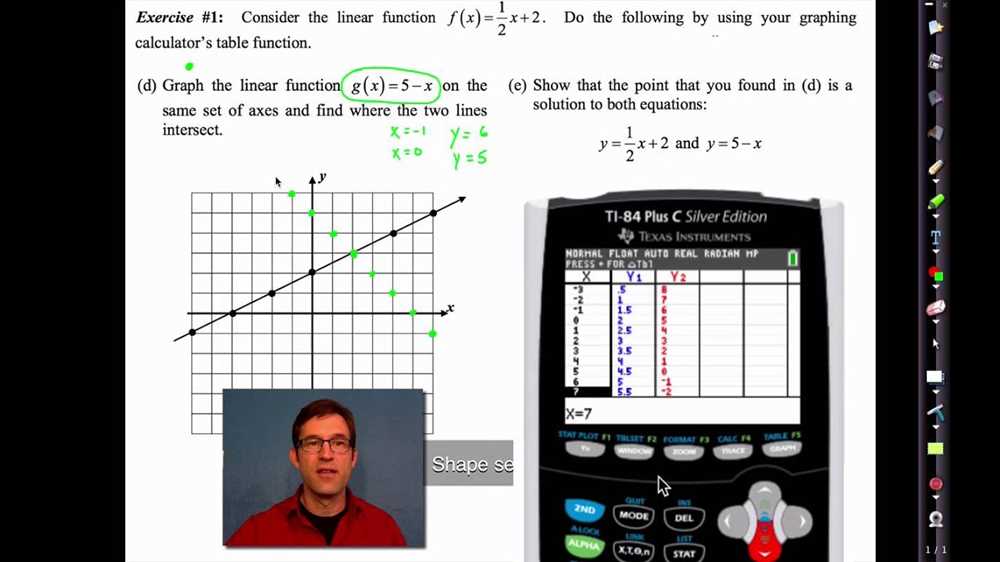
In mathematics, a linear relationship is a mathematical expression that can be represented by a straight line on a graph. It is a relationship between two variables that can be expressed as y = mx + b, where y represents the dependent variable, x represents the independent variable, m represents the slope, and b represents the y-intercept.
A linear relationship can be visualized on a Cartesian coordinate system, with the independent variable plotted on the x-axis and the dependent variable plotted on the y-axis. The line that represents the relationship connects all the points that satisfy the equation y = mx + b. This line has a constant slope, meaning that for every unit increase in the independent variable, the dependent variable will increase or decrease by a fixed amount.
One key characteristic of a linear relationship is that the ratio between the change in the dependent variable to the change in the independent variable remains constant throughout the relationship. This ratio is represented by the slope of the line, m. A positive slope indicates a direct relationship, where an increase in the independent variable leads to an increase in the dependent variable. A negative slope indicates an inverse relationship, where an increase in the independent variable leads to a decrease in the dependent variable.
The y-intercept, represented by the constant b in the equation, determines the starting point of the line on the y-axis. It is the value of the dependent variable when the independent variable is equal to zero. The y-intercept provides valuable information about the initial condition or baseline of the relationship.
In conclusion, a linear relationship is a mathematical expression that can be represented by a straight line and follows a specific equation. It is characterized by a constant ratio between the change in the dependent and independent variables, represented by the slope, and has a starting point determined by the y-intercept. Understanding and analyzing linear relationships is essential in various fields of study, including mathematics, physics, economics, and engineering.
Examples of Linear Relationships
In mathematics, a linear relationship refers to a straight-line relationship between two variables. This means that as one variable increases, the other variable also increases at a consistent rate. Linear relationships are commonly seen in various fields, such as physics, economics, and statistics. Here are a few examples of linear relationships:
Example 1: Distance Traveled over Time
Suppose you are driving a car at a constant speed. The distance you travel is directly proportional to the amount of time you spend driving. In this case, the relationship between distance and time is linear. For example, if you drive for 2 hours, you will travel twice as far as if you had driven for 1 hour.
Example 2: Cost of a Product based on Quantity
Let’s say you are purchasing apples from a grocery store. The cost of the apples is $2 per pound. In this case, the relationship between the cost and the quantity of apples is linear. If you buy 3 pounds of apples, the cost will be 3 times the cost of 1 pound of apples.
Example 3: Population Growth over Time
When studying population trends, it is common to observe linear relationships. For instance, the population of a city may increase by a certain number of people each year. In this case, the relationship between population and time is linear. If the city’s population increases by 1000 people every year, after 5 years, the population will have increased by 5000 people.
These examples demonstrate how linear relationships can be found in various real-world scenarios. By understanding and recognizing linear relationships, we can make predictions, analyze trends, and solve problems in different fields of study.
Solving Linear Equations

Linear equations are mathematical equations that involve variables raised to the power of 1. Solving linear equations is an essential skill in algebra and plays a crucial role in various real-world applications.
To solve a linear equation, the goal is to isolate the variable on one side of the equation. This is done by performing various operations on both sides of the equation to maintain equality. The basic operations used are addition, subtraction, multiplication, and division.
When solving linear equations, it is important to follow a systematic approach. Start by simplifying both sides of the equation, using the distributive property if necessary. Combine like terms and then isolate the variable term by performing the inverse operation on both sides. The inverse operation undoes the effect of the original operation.
It is important to note that when solving linear equations, both sides of the equation should always remain equal. This means that any operation performed on one side must also be performed on the other side. By carefully following these steps, one can find the value of the variable that satisfies the equation.
Linear equations can be solved using different methods, such as graphing, substitution, or elimination. Each method has its own advantages and may be more suitable for certain situations. The choice of method depends on the given equation and the desired outcome.
In conclusion, solving linear equations is a fundamental skill in mathematics. It allows us to find the values of variables that make an equation true. By following a systematic approach and using appropriate methods, we can successfully solve linear equations and apply them to a wide range of practical problems.
Graphing Linear Equations
Graphing linear equations is an essential skill in mathematics, as it allows us to visualize and analyze the relationships between variables. A linear equation is an equation that represents a straight line on a graph, and it can be written in the form y = mx + b. Here, m represents the slope of the line, and b represents the y-intercept, which is the point where the line intersects the y-axis.
To graph a linear equation, we need to plot at least two points on the graph and then connect them with a straight line. One way to find these points is by using the slope-intercept form of the equation. By identifying the slope and y-intercept, we can easily determine two points that lie on the line.
Example:
If we have the equation y = 2x + 3, we can start by plotting the y-intercept, which is the point (0, 3) since the y-intercept is the value of y when x = 0. Then, using the slope of 2, we can determine a second point by moving 2 units up and 1 unit to the right from the y-intercept, resulting in the point (1, 5). Finally, we can connect these two points with a straight line to graph the equation.
Graphing linear equations is a fundamental skill in algebra, and it allows us to analyze and interpret the relationships between variables visually. By understanding the concepts of slope and y-intercept, we can easily graph linear equations and gain valuable insights into the patterns and trends they represent.
Finding Slope and Y-Intercept
In linear equations, the slope refers to the steepness of the line, while the y-intercept represents the point where the line intersects the y-axis. These two values are essential in determining the equation of a line and understanding its characteristics.
To find the slope of a line, you can use the formula:
slope = change in y / change in x
Here, “change in y” refers to the difference in the y-values of two points on the line, and “change in x” represents the difference in their corresponding x-values. By calculating this ratio, you can determine how the y-values on the line change in relation to the x-values.
The y-intercept, on the other hand, is the value of y when x is equal to zero. It represents the point where the line crosses the y-axis. To find the y-intercept, you can identify the point where the line intersects the y-axis or use the equation:
y-intercept = y – (slope * x)
By substituting the values of a point on the line, such as the coordinates (x, y), and the slope of the line into this equation, you can calculate the y-intercept.
Understanding the slope and y-intercept of a linear equation helps in graphing the line, finding its equation in slope-intercept form (y = mx + b), and interpreting its meaning in a real-world context.
Applications of Linear Relationships
Linear relationships are fundamental in various real-world applications, allowing us to model and understand the relationships between different variables. By studying linear relationships, we can analyze how one variable changes in relation to another and make predictions based on this understanding.
One common application of linear relationships is in the field of physics. For example, when studying motion, we can use linear relationships to describe the relationship between an object’s displacement and time. This allows us to calculate the object’s velocity and acceleration, which are crucial in understanding its motion.
In economics, linear relationships are frequently used to analyze supply and demand. By establishing a linear relationship between the price of a product and the quantity demanded or supplied, economists can determine price elasticity, forecast market trends, and make informed decisions regarding pricing and production levels.
Linear relationships also play a crucial role in engineering. For instance, engineers use linear relationships to design efficient electrical systems by analyzing the relationship between voltage, current, and resistance. This helps ensure that the electrical components function optimally and minimize energy waste.
In data analysis, linear relationships are often used to draw meaningful conclusions and predictions. By fitting a set of data points to a straight line, statisticians can analyze trends and make predictions based on the observed patterns.
Overall, linear relationships have countless applications in various fields, enabling us to understand, predict, and make informed decisions in a wide range of situations. By studying and analyzing these relationships, we can continue to make advancements in science, technology, economics, and other disciplines.
Practice Problems and Answer Key
Here are some practice problems to help you further understand linear relationships. Use the answer key below to check your solutions.
Problem 1:

Find the slope of the line passing through the points (2,-3) and (4,5).
Problem 2:
Write the equation of a line that passes through the point (3,7) and has a slope of -2.
Problem 3:
Graph the line with the equation y = 2x + 3.
Answer Key:
- Problem 1: The slope of the line is 4.
- Problem 2: The equation of the line is y = -2x + 13.
- Problem 3: The line is a straight line that passes through the point (0,3) and has a slope of 2.
Use these practice problems and the answer key to improve your understanding of linear relationships. Remember to always double-check your solutions to ensure accuracy.