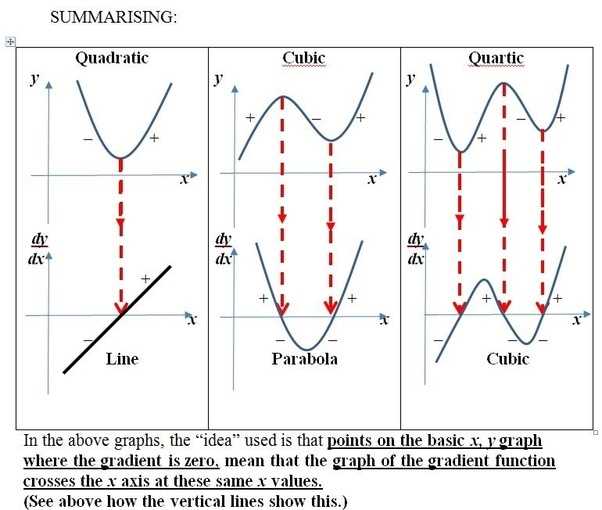
When studying calculus, one of the key concepts to understand is the relationship between a function and its derivative. The derivative of a function represents the rate of change of the function at any given point. Graphing the derivative can provide valuable insights into the behavior of the original function.
Matching derivative graphs to their corresponding functions is a common exercise in calculus courses. It helps students develop an intuitive understanding of how changes in the original function are reflected in its derivative. By analyzing the shape and characteristics of the derivative graph, one can make educated guesses about the behavior of the original function.
However, matching derivative graphs can be a challenging task, as there are infinite possibilities for the shape of a derivative graph given a particular original function. It requires a deep understanding of calculus concepts, such as the chain rule, product rule, and quotient rule, to accurately determine the derivative of a function and its corresponding graph.
In order to successfully match derivative graphs, it is important to analyze key characteristics such as the presence of critical points, inflection points, and local maximums or minimums. Understanding how these features manifest in both the original function and its derivative can greatly assist in finding the correct match.
Matching Derivative Graphs Answers
The concept of matching derivative graphs can be challenging, but with the right approach, it becomes manageable. Here are some answers to help you correctly match derivative graphs:
Graph 1:
The first graph represents the derivative of a constant function. The derivative of a constant function is always zero. This graph is a horizontal line at zero, indicating that the rate of change is constant and equal to zero.
Graph 2:
Graph 2 represents the derivative of a linear function. The derivative of a linear function is a constant value equal to the slope of the line. In this case, the graph is a horizontal line at a non-zero value, showing that the rate of change is constant throughout.
Graph 3:
Graph 3 represents the derivative of a quadratic function. The derivative of a quadratic function is a linear function. This graph shows a linearly increasing or decreasing slope, indicating that the rate of change is not constant but varies with x.
Graph 4:

Graph 4 represents the derivative of an exponential function. The derivative of an exponential function is proportional to the original function itself. This graph shows exponential growth or decay, with the rate of change increasing or decreasing with x.
Graph 5:
Graph 5 represents the derivative of a logarithmic function. The derivative of a logarithmic function decreases for larger x values. This graph shows a decreasing slope, indicating that the rate of change diminishes as x increases.
It’s essential to understand the properties and behavior of different functions to correctly match derivative graphs. Practice analyzing the patterns and understanding the concept of derivatives to improve your ability to match derivative graphs accurately.
The Concept of Derivatives
The concept of derivatives is fundamental in calculus and plays a crucial role in understanding the rate of change of a function at any given point. A derivative represents the slope of the tangent line to the graph of a function at a specific point and provides valuable insights into the behavior of functions.
One way to think about derivatives is to consider them as the instantaneous rate of change. When we calculate the derivative of a function, we are essentially determining how fast the function is changing at any given point. This allows us to study and analyze the behavior of functions with precision.
The derivative of a function can be understood as the limit of the average rate of change of the function as the interval over which the change is measured approaches zero. In other words, we are interested in the rate at which the function is changing at an infinitesimally small scale. This limit is denoted using the notation dy/dx or f'(x), where y represents the dependent variable and x represents the independent variable of the function.
Derivatives have numerous applications in various fields such as physics, economics, engineering, and more. They are used to model and analyze real-world phenomena, optimize processes, determine maximum and minimum values, and understand the behavior of functions in dynamic systems. Derivatives also have connections to other mathematical concepts such as integrals, which together form the foundation of calculus.
In summary, the concept of derivatives is essential for understanding the rate of change of functions and provides insights into the behavior of functions at specific points. Derivatives are used in a wide range of applications and have deep connections to other areas of mathematics. They allow us to study and analyze functions with precision and provide valuable tools for solving real-world problems.
Understanding Graphical Representations of Derivatives
Graphical representations of derivatives are essential tools in understanding the behavior of functions and their rates of change. These representations provide visual insights into how the function changes at different points and help in identifying key features such as critical points and inflection points.
One common graphical representation of derivatives is the derivative graph, which shows the slope of the original function at each point. The slope of a function represents the rate of change, and the derivative graph allows us to see how this rate changes throughout the function’s domain. Points where the derivative is zero indicate critical points, where the function may have a maximum or minimum value. Furthermore, the derivative graph can reveal information about the concavity of the function, such as inflection points where the concavity changes.
Another graphical representation of derivatives is the tangent line. The tangent line at a given point on a function represents the instantaneous rate of change at that point. By analyzing the slope of the tangent line, we can determine whether the function is increasing or decreasing and how quickly it is doing so. This information is crucial for understanding the behavior of the function and making predictions about its future values.
- Understanding graphical representations of derivatives is essential in various fields such as physics, engineering, and economics. In physics, for example, the derivative graph of a position-time function can provide insights into the velocity and acceleration of an object. In economics, derivative graphs of cost and revenue functions help in analyzing profit maximization strategies.
- When interpreting graphical representations of derivatives, it is crucial to consider the context and the behavior of the original function. For example, a steep slope in the derivative graph may indicate a rapid change in the original function, while a flat slope may suggest a constant rate of change or a maximum/minimum point.
- Overall, understanding the graphical representations of derivatives allows us to gain a deeper understanding of functions and their behavior. These representations provide valuable insights into rates of change, critical points, and concavity, enabling us to make more informed decisions and predictions in various fields.
How to Match Derivative Graphs to Functions

Matching derivative graphs to functions is an important skill in calculus. It involves analyzing the shape and characteristics of the derivative graph to determine which function it represents. Here are some steps to help you match derivative graphs to functions:
1. Identify key features
Start by identifying the key features of the derivative graph, such as any local extrema (maximum or minimum points), points of inflection, and intervals of increasing or decreasing slopes. These features can give you clues about the behavior of the original function.
2. Consider the slope
The slope of the derivative graph represents the rate of change of the original function. If the derivative graph has a positive slope, it means the original function is increasing. If the derivative graph has a negative slope, it means the original function is decreasing.
Additionally, the steepness of the slope can give you information about the steepness of the original function. A steeper slope in the derivative graph indicates a faster rate of change in the original function.
3. Examine concavity
The concavity of the derivative graph can help you determine the concavity of the original function. If the derivative graph is concave up (opening upwards), it means the original function is concave up. If the derivative graph is concave down (opening downwards), it means the original function is concave down.
4. Use known functions
Compare the key features and characteristics of the derivative graph to the known graphs of common functions. For example, the derivative graph of a linear function will be a constant line, while the derivative graph of an exponential function will be an increasing curve.
By analyzing the key features, slope, and concavity of the derivative graph, and comparing them to known functions, you can match derivative graphs to functions more effectively. Practice and familiarity with different functions and their derivatives will improve your ability to make accurate matches.
Recognizing Key Characteristics of Derivative Graphs
The graph of a derivative function can provide valuable information about the original function. By examining the key characteristics of derivative graphs, mathematicians can gain insights into the behavior and properties of the corresponding functions. Recognizing these characteristics can help in solving related problems and understanding the overall behavior of functions.
1. Slope of the tangent line: One of the most important characteristics of a derivative graph is the slope of the tangent line at each point. The slope of the tangent line represents the rate of change of the original function at that particular point. Positive slopes indicate increasing values, negative slopes indicate decreasing values, and horizontal slopes represent extrema or points of inflection.
2. Zeroes and critical points: The points where the derivative graph crosses the x-axis are known as zeroes or roots of the derivative function. These correspond to critical points of the original function, where the function reaches a local maximum, minimum, or point of inflection. By identifying and analyzing these points, mathematicians can determine the behavior and shape of the original function.
3. Concavity: The concavity of a derivative graph refers to the direction in which the graph curves. A positive concavity indicates that the original function is concave up, while a negative concavity indicates a concave down shape. Points of inflection occur where the concavity changes. Understanding the concavity of the derivative graph helps in visualizing the shape of the original function.
4. Relative maxima and minima: Local maxima and minima of the original function can be identified by observing turning points on the derivative graph. The derivative graph shows when the original function changes from increasing to decreasing (maxima) or decreasing to increasing (minima). These points are crucial for determining the behavior and extreme values of the original function.
By utilizing these key characteristics and analyzing the derivative graph, mathematicians can deduce valuable information about the corresponding original function. Whether it’s understanding rates of change, critical points, concavity, or extreme values, the derivative graph is a powerful tool for investigating and solving problems related to functions.
Identifying Slope and Concavity in Derivative Graphs
When analyzing derivative graphs, it is important to understand how to identify the slope and concavity of the original function. The derivative graph represents the rate of change of the function at each point, and knowing the slope and concavity can provide valuable information about the behavior of the function.
Slope: The slope of the derivative graph can be determined by examining the steepness of the line at different points. A steeper line indicates a higher rate of change, while a flatter line indicates a lower rate of change. Positive slopes indicate that the function is increasing, while negative slopes indicate a decreasing function. A horizontal line indicates zero slope, which means the function has reached a maximum or minimum point.
Concavity: Concavity refers to the shape of the derivative graph and reveals whether the original function is concave up or concave down. A concave up graph has a positive concavity and resembles a cup or a smiley face, with the derivative increasing at an increasing rate. Conversely, a concave down graph has a negative concavity and resembles a frown or a frown face, with the derivative increasing at a decreasing rate. Inflection points occur when the concavity changes from positive to negative or vice versa, and they indicate points where the behavior of the function changes.
To identify slope and concavity in derivative graphs, it is helpful to look for key features such as maxima, minima, points of inflection, and regions of increasing or decreasing slope. By understanding the relationship between the derivative graph and the original function, one can gain insights into the behavior of the function and make predictions about its characteristics.
Recognizing Transition Points and Inflection Points
When analyzing the graph of a derivative function, one important aspect to consider is the presence of transition points and inflection points. Transition points occur at the x-values where the derivative changes sign, indicating a change in the direction of the original function. Inflection points, on the other hand, occur at the x-values where the concavity of the original function changes.
Recognizing transition points is crucial for understanding the behavior of the original function. If the derivative changes sign at a specific x-value, it means that the original function is switching from increasing to decreasing or vice versa at that point. This information can be used to determine critical points, local maxima, or local minima of the original function.
Similarly, identifying inflection points helps in understanding the shape of the original function. At an inflection point, the concavity of the original function changes from being concave up to concave down, or vice versa. This can indicate the presence of a point of inflection, where the original function may have a change in its concavity or even a change in its overall behavior.
To recognize transition points and inflection points, it is essential to study the behavior of the derivative function, focusing on the sign changes and the concavity changes. By analyzing these patterns and comparing them to the original function, it becomes possible to gain insights into the overall behavior and characteristics of the function.