
In the study of geometry, an important concept is the idea of triangles and their congruence. Understanding the properties and relationships of triangles is crucial for solving various geometric problems. In Unit 6 of Math 2, we explore the different ways to determine if two triangles are congruent and the various postulates and theorems that can be used to prove their congruence.
One of the key methods used in determining triangle congruence is the Side-Angle-Side (SAS) postulate. This postulate states that if two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the triangles are congruent. By using this postulate, we can determine whether two triangles are identical in shape and size.
Another important postulate is the Angle-Angle-Side (AAS) postulate. This postulate states that if two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then the triangles are congruent. By utilizing the AAS postulate, we can establish the congruence of triangles by comparing their angles and sides.
Math 2 Unit 6 Triangles and Congruence Answer Key: Everything You Need to Know
If you are studying Math 2 and currently learning about triangles and congruence, having access to a comprehensive answer key can greatly supplement your learning experience. Understanding the concepts and mastering the skills related to triangles and congruence is crucial for success in geometry and many other areas of mathematics.
The Math 2 Unit 6 Triangles and Congruence Answer Key provides you with all the correct answers and explanations for the exercises and problems in the unit. It serves as a valuable resource that can help you check your work, understand the steps needed to solve a problem, and clarify any confusion you may have.
With the answer key, you can easily review and practice various topics covered in the unit, such as triangle congruence postulates and theorems (SSS, SAS, ASA, AAS), triangle congruence proofs, and applying triangle congruence to real-life situations. The key also includes examples and additional practice problems to reinforce your understanding and improve your problem-solving skills.
By utilizing the Math 2 Unit 6 Triangles and Congruence Answer Key, you can confidently approach your assignments, quizzes, and tests, knowing that you have a reliable tool to help you navigate through the material. It allows you to self-assess your progress, identify areas that may need more attention, and ultimately achieve a deeper understanding of the principles and concepts related to triangles and congruence.
Whether you are a student, teacher, or anyone interested in mastering the concepts of triangles and congruence, the Math 2 Unit 6 Triangles and Congruence Answer Key is a valuable resource that can enhance your learning experience and help you succeed in your mathematical journey.
Understanding Triangles and Congruence
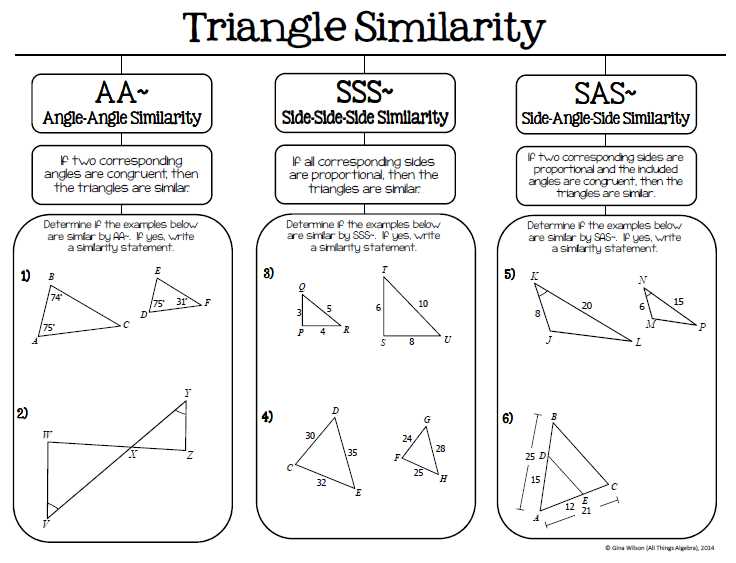
Triangles are one of the fundamental shapes in geometry, and understanding their properties and relationships is essential in mathematics. When studying triangles, one important concept to grasp is congruence. Congruent triangles are triangles that have the same size and shape, regardless of their orientation or position.
To determine if two triangles are congruent, several methods can be used. One method is the Side-Side-Side (SSS) congruence postulate, which states that if the three sides of one triangle are congruent to the corresponding sides of another triangle, then the triangles are congruent. Another method is the Side-Angle-Side (SAS) congruence postulate, which states that if two sides and the included angle of one triangle are congruent to the corresponding parts of another triangle, then the triangles are congruent.
Once the congruence of triangles is established, numerous properties and theorems can be applied. For example, the corresponding angles and sides of congruent triangles are equal, and the sum of the angles in a triangle is always 180 degrees. Additionally, congruent triangles can be used to prove other geometric relationships, such as the fact that the medians of a triangle intersect at a single point called the centroid.
Overall, understanding triangles and congruence is crucial for solving geometry problems and exploring the intricacies of shapes and their properties. By mastering the concepts and techniques related to triangles and congruence, students can develop a strong foundation in geometry and apply their knowledge to various mathematical situations.
Properties of Congruent Triangles
Congruent triangles are triangles that have the same size and shape. When two triangles are congruent, it means that their corresponding sides and angles are equal. Understanding the properties of congruent triangles is essential for solving geometry problems and proving the congruence of different shapes.
One property of congruent triangles is the side-side-side (SSS) criterion. This criterion states that if the three sides of one triangle are congruent to the three sides of another triangle, then the two triangles are congruent. This property can be used to determine the congruence of triangles when their side lengths are known.
Another property of congruent triangles is the angle-side-angle (ASA) criterion. According to this criterion, if two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then the two triangles are congruent. This property allows us to prove the congruence of triangles when their angle measures and side lengths are given.
Additionally, the side-angle-side (SAS) criterion is another property of congruent triangles. This criterion states that if two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the two triangles are congruent. This property is useful for proving the congruence of triangles based on partial information about their sides and angles.
In conclusion, the properties of congruent triangles, such as the SSS, ASA, and SAS criteria, provide a framework for determining when two triangles are congruent. These properties are fundamental in geometry and enable us to solve various problems and prove the congruence of different shapes.
Methods to Prove Triangle Congruence
When studying triangles and congruence in math, there are several methods that can be used to prove that two triangles are congruent. These methods, also known as congruence postulates, rely on different sets of information about the triangles to establish their congruence.
One of the most commonly used methods to prove triangle congruence is the Side-Side-Side (SSS) postulate. This postulate states that if three sides of one triangle are congruent to the corresponding sides of another triangle, then the two triangles are congruent. This can be proven by using the fact that if the three sides of a triangle are equal in length to the corresponding sides of another triangle, then all corresponding angles will also be congruent.
Another method is the Side-Angle-Side (SAS) postulate, which states that if two sides and the included angle of one triangle are congruent to the corresponding parts of another triangle, then the two triangles are congruent. This postulate can be proven by the Angle-Side-Angle (ASA) postulate, which states that if two angles and the included side of one triangle are congruent to the corresponding parts of another triangle, then the two triangles are congruent.
In addition, the Hypotenuse-Leg (HL) postulate can be used to prove congruence in right triangles. This postulate states that if the hypotenuse and one leg of a right triangle are congruent to the corresponding parts of another right triangle, then the two triangles are congruent.
Overall, these methods provide a systematic way to determine whether two triangles are congruent based on their sides and angles. By applying the appropriate postulate or theorem, mathematicians can confidently establish the congruence of triangles in various geometric problems.
Congruence Theorems and Postulates
Congruence theorems and postulates are fundamental concepts in geometry that allow us to prove that two figures are congruent. Congruent figures are identical in shape and size, meaning that all corresponding sides and angles are equal. These theorems and postulates provide a systematic approach to determining congruence.
One of the most basic congruence postulates is the Side-Side-Side (SSS) postulate, which states that if three sides of one triangle are congruent to three sides of another triangle, then the two triangles are congruent. This postulate can be used to prove congruence by comparing the lengths of the sides of the triangles.
Another important congruence theorem is the Angle-Side-Angle (ASA) theorem, which states that if two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then the two triangles are congruent. This theorem relies on the fact that the included side is the side between the two given angles.
The Hypotenuse-Leg (HL) theorem is another congruence postulate that is specifically applicable to right triangles. It states that if the hypotenuse and one leg of a right triangle are congruent to the hypotenuse and one leg of another right triangle, then the two right triangles are congruent. The HL theorem is used to prove congruence when dealing with right triangles.
By using these and other congruence theorems and postulates, we can determine whether two figures are congruent or not. These concepts form the basis of many geometric proofs and help us understand the relationships between different shapes and figures.
Summary:
- Congruence theorems and postulates allow us to prove that two figures are congruent.
- The Side-Side-Side (SSS) postulate states that if three sides of one triangle are congruent to three sides of another triangle, then the two triangles are congruent.
- The Angle-Side-Angle (ASA) theorem states that if two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then the two triangles are congruent.
- The Hypotenuse-Leg (HL) theorem is specifically applicable to right triangles and states that if the hypotenuse and one leg of a right triangle are congruent to the hypotenuse and one leg of another right triangle, then the two right triangles are congruent.
Solved Examples and Practice Problems
Here are some solved examples and practice problems on triangles and congruence, which will help you understand and apply the concepts in this unit:
Solved Example 1:
Question: In triangle ABC, angle A is 50 degrees and angle B is 60 degrees. Find angle C.
Solution: Since the sum of angles in a triangle is 180 degrees, we can find angle C by subtracting the sum of angles A and B from 180:
C = 180 – (50 + 60) = 180 – 110 = 70 degrees
Solved Example 2:
Question: Triangle PQR is congruent to triangle XYZ. If angle P is equal to angle Y and side PR is equal to side XZ, what can we conclude about the triangles?
Solution: Based on the given information, we can conclude that the triangles are congruent by the Side-Angle-Side (SAS) congruence criterion. This means that all corresponding sides and angles of the two triangles are equal.
Practice Problems:
- In triangle ABC, angle A is 40 degrees and angle B is 80 degrees. Find angle C.
- Triangle PQR is congruent to triangle STU. If side PQ is equal to side ST and angle R is equal to angle U, what can we conclude about the triangles?
- In triangle XYZ, angle X is 70 degrees and angle Y is 90 degrees. Find angle Z.
- Triangle ABC is congruent to triangle DEF. If side BC is equal to side EF and angle B is equal to angle D, what can we conclude about the triangles?
Try to solve these practice problems on your own, and then check your answers. By practicing more problems, you will enhance your understanding of triangles and congruence.
Applying Triangle Congruence to Real-world Scenarios
In the study of geometry, triangle congruence is a fundamental concept that has practical applications in real-world scenarios. When we say that two triangles are congruent, it means that they have the same size and shape. This concept is useful in a variety of fields, such as architecture, engineering, and navigation.
Architects often use triangle congruence to ensure the structural integrity of buildings. By applying the principles of congruent triangles, they can analyze the stability and balance of various structures. For example, if two triangles are congruent, we can conclude that the corresponding sides and angles of the triangles are also congruent. This knowledge allows architects to design stable and visually pleasing buildings.
In engineering, triangle congruence is essential for analyzing and designing mechanical systems. By understanding the properties of congruent triangles, engineers can optimize the placement of components, reduce stress on materials, and improve the overall performance of machines. The principles of triangle congruence also apply to the field of robotics, where precise measurements and calculations are necessary for the accurate movement and positioning of robotic arms and manipulators.
In navigation, triangle congruence plays a crucial role in determining distances and angles. The principles of congruent triangles are used in triangulation, a method that involves measuring the angles and sides of a triangle to determine the position of an object. Triangulation is commonly used in surveying, cartography, and GPS systems to determine the exact location of landmarks, map boundaries, and navigate accurately.
In conclusion, the application of triangle congruence to real-world scenarios is essential in various fields. Whether it’s in architecture, engineering, or navigation, the principles of congruent triangles enable professionals to analyze, design, and navigate with precision and accuracy. Understanding triangle congruence allows us to make informed decisions and solve practical problems in our everyday lives.