
The concept of mole ratio is an essential part of chemistry, particularly when it comes to stoichiometry. Stoichiometry is the calculation of the quantities of reactants and products in a chemical reaction. Mole ratio is the relationship between the amounts of substances involved in a chemical equation, based on the coefficients in the balanced equation.
Understanding and applying mole ratios is crucial in stoichiometry problems, as it allows chemists to determine the amount of one substance based on the known amount of another. It helps in predicting the amount of product that can be formed or the amount of reactant that is needed in a given chemical reaction.
In this article, we provide the mole ratio practice answer key to guide students in solving stoichiometry problems involving mole ratios. By going through the provided answers, students can check their understanding of mole ratios and familiarize themselves with the process of applying them to stoichiometry calculations. This answer key serves as a valuable resource for students as they practice and reinforce their knowledge of mole ratios in chemistry.
Mole Ratio Practice Answer Key
When it comes to understanding mole ratios, practice is essential. Having the answer key for mole ratio practice problems can be helpful in determining if your calculations are correct and ensuring a deeper understanding of the concept. In chemistry, mole ratios represent the relationships between the amounts of different substances involved in a chemical reaction. These ratios are derived from the balanced equation of the reaction.
The mole ratio answer key provides the correct ratios for converting between moles of different substances in a given chemical equation. By comparing your calculations to the answer key, you can identify any mistakes or errors in your work. It is important to understand that mole ratios are used to convert from one substance to another, allowing you to determine the amounts of reactants and products in a reaction.
The answer key for mole ratio practice problems typically includes the correct ratios for each substance involved in the reaction. This allows you to calculate the moles of one substance based on the known moles of another substance. It is crucial to remember that the ratio is based on the coefficients in the balanced equation, as these coefficients represent the relative number of moles of each substance involved.
Overall, having an answer key for mole ratio practice problems can greatly assist in reinforcing your understanding of mole ratios and their application in chemical reactions. By practicing with these problems and comparing your answers to the answer key, you can enhance your skills in stoichiometry and accurately determine the amounts of substances involved in a reaction.
What are Mole Ratios in Chemistry?
Mole ratios are an important concept in chemistry that helps to understand the quantitative relationships between different substances in a chemical reaction. A mole ratio represents the ratio of the number of moles of one substance to another substance in a balanced equation.
In a chemical reaction, the reactants are often combined in specific stoichiometric proportions to produce the desired products. The balanced equation for the reaction shows the ratio of the reactants and products in terms of moles. This ratio is crucial for determining the amount of each substance involved in the reaction.
Mole ratios can be used in various calculations, such as determining the limiting reactant, predicting the amount of product formed, and calculating the amount of excess reactant left over. By using the mole ratio, it is possible to convert between moles of one substance and moles of another substance in a given reaction.
The mole ratio is obtained from the coefficients of the balanced equation. For example, if the balanced equation shows that 2 moles of substance A react with 3 moles of substance B to produce 4 moles of substance C, the mole ratio between A and B is 2:3, and the mole ratio between A and C is 2:4 or simplified as 1:2. These ratios are useful for determining the relative amounts of substances involved in the reaction.
Overall, mole ratios play a crucial role in understanding and quantifying chemical reactions. They provide a way to relate the amounts of reactants and products in a reaction and allow for accurate calculations and predictions in chemistry experiments and processes.
Importance of Mole Ratios in Chemical Reactions
The concept of mole ratio is fundamental to understanding and predicting the outcome of chemical reactions. Mole ratio refers to the ratio of the number of moles of one substance to the number of moles of another substance in a balanced chemical equation. It provides crucial information about the stoichiometry of a reaction, allowing chemists to determine the amounts of reactants and products involved in a chemical process.
Mole ratios are essential for calculating the quantities of reactants needed to obtain a desired amount of product or vice versa. By using mole ratios, chemists can convert between mass, moles, and volume of substances involved in a reaction, enabling them to perform accurate measurements and make precise calculations. This knowledge is vital not only for laboratory experiments but also for industrial processes, where efficiency and cost-effectiveness are key considerations.
Mole ratios also play a crucial role in determining the limiting reactant in a chemical reaction. The limiting reactant is the substance that is completely consumed in the reaction, limiting the amount of product that can be formed. By comparing the mole ratios of the reactants, chemists can identify which reactant will be completely used up first and calculate the theoretical yield of the product.
Furthermore, mole ratios help chemists understand the theoretical and percent yield of a reaction. The theoretical yield is the maximum amount of product that can be obtained based on the stoichiometry of the reaction, while the percent yield represents the actual amount of product obtained compared to the theoretical yield. Mole ratios allow chemists to calculate these values and assess the efficiency of their reactions.
In summary, the concept of mole ratios is essential for understanding the stoichiometry of chemical reactions, calculating reactant and product quantities, determining limiting reactants, and evaluating the efficiency of reactions. It serves as a fundamental tool for chemists in various fields, from laboratory research to industrial production, enabling them to make accurate measurements, perform precise calculations, and optimize their processes.
How to Calculate Mole Ratios
When working with chemical reactions and stoichiometry, it is important to understand how to calculate mole ratios. A mole ratio is the ratio between the number of moles of any two substances in a balanced chemical equation. It allows us to determine the amount of one substance that is needed to react completely with a given amount of another substance.
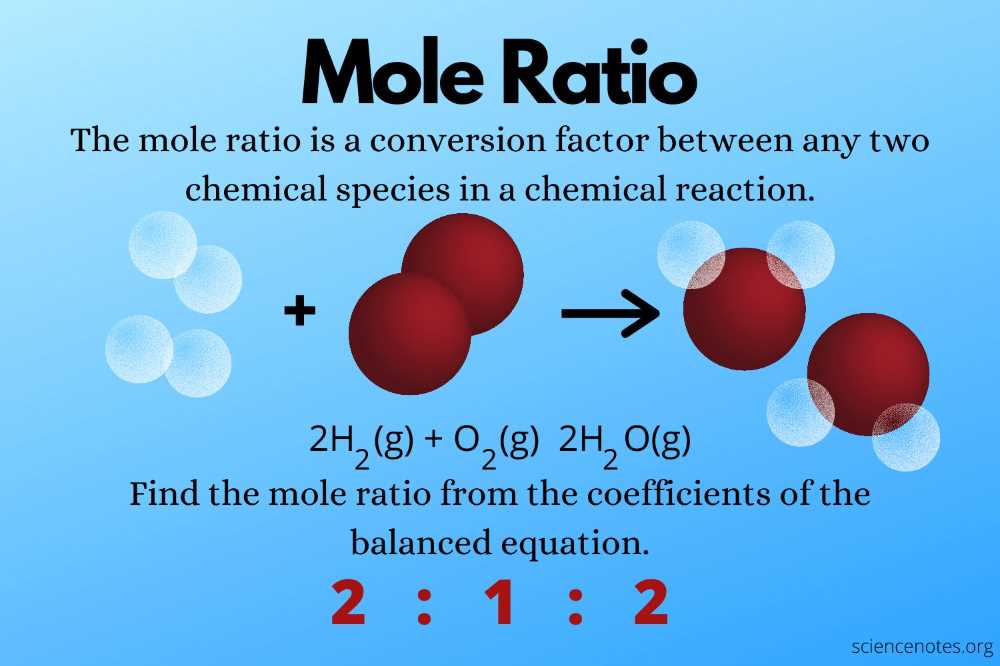
To calculate the mole ratio, you need a balanced chemical equation. The coefficients in the equation represent the mole ratios. For example, in the balanced equation 2H2 + O2 → 2H2O, the mole ratio between H2 and O2 is 2:1. This means that for every 2 moles of H2, you need 1 mole of O2 to react completely.
To calculate the mole ratio between two substances, you can divide the coefficients of the substances in the balanced equation. In the example above, you would divide the coefficient of H2 by the coefficient of O2 to get the mole ratio. In this case, it would be 2/1 = 2.
Mole ratios are essential for performing stoichiometric calculations, such as determining the limiting reactant or the amount of product formed in a reaction. They help ensure that the reaction proceeds as expected and allow chemists to accurately predict the outcomes of chemical reactions.
Practice Problems for Mole Ratio Calculations
In chemistry, mole ratio calculations are an important tool for understanding and predicting chemical reactions. By determining the ratio of moles of reactants and products in a balanced chemical equation, scientists can make accurate predictions about how much of each substance will be involved in a reaction.
To practice mole ratio calculations, it is important to start with a balanced chemical equation that represents the reaction of interest. The coefficients within the equation indicate the mole ratio between the substances involved. For example, in the equation: 2H2 + O2 -> 2H2O, the mole ratio between hydrogen and oxygen is 2:1.
One common practice problem involves determining the amount of one substance based on the known amount of another substance. For example, given the reaction: 2Al + 3Br2 -> 2AlBr3, if we have 4 moles of aluminum (Al), we can use the mole ratio to determine the number of moles of bromine (Br2) needed for the reaction.
- Step 1: Determine the mole ratio from the balanced chemical equation. In this case, the mole ratio between aluminum and bromine is 2:3.
- Step 2: Set up a proportion using the known amount of aluminum and an unknown amount of bromine. For example: (2 moles Al / 3 moles Br2) = (4 moles Al / x moles Br2).
- Step 3: Solve the proportion for “x” to determine the number of moles of bromine needed.
By practicing these types of problems, students can improve their understanding of mole ratios and their ability to calculate the amount of substances involved in chemical reactions. It is important to remember to always use a balanced chemical equation and pay close attention to the mole ratio within the equation.
Step-by-Step Solutions for Mole Ratio Practice Problems
When it comes to solving mole ratio practice problems, it’s important to follow a step-by-step approach to ensure accuracy and clarity. By following these steps, you can confidently solve mole ratio problems and understand the relationship between different substances in a chemical equation.
Step 1: Write the Balanced Chemical Equation
The first step in solving mole ratio problems is to write the balanced chemical equation. This equation shows the reactants and products involved in the chemical reaction. Be sure to include the correct coefficients for each substance to maintain balance.
Step 2: Determine the Given Quantity
Next, determine the given quantity in the problem. This could be the number of moles, mass, or volume of a substance involved in the reaction. Make sure to convert any given units to moles if necessary.
Step 3: Identify the Mole Ratio
Identify the mole ratio between the given substance and the desired substance. The mole ratio is determined by the coefficients in the balanced chemical equation. It represents the number of moles of one substance that reacts with or produces another substance.
Step 4: Use the Mole Ratio to Calculate the Desired Quantity
Using the mole ratio, calculate the desired quantity of the substance. Multiply the given quantity by the mole ratio to find the number of moles of the desired substance. If necessary, convert the moles back to the desired units, such as mass or volume, using the appropriate conversion factors.
Step 5: Check the Units and Significant Figures
Finally, check the units and significant figures in your final answer. Make sure the units are consistent and the number of significant figures is appropriate for the given problem. Round your final answer to the correct number of significant figures.
By following these step-by-step solutions for mole ratio practice problems, you can effectively solve these problems and develop a strong understanding of the relationships between substances in chemical equations.
Common Mistakes to Avoid when Calculating Mole Ratios
Calculating mole ratios is a fundamental skill in chemistry, as it allows us to determine the stoichiometry of a chemical reaction. However, there are some common mistakes that students often make when performing these calculations. It is important to be aware of these mistakes and take steps to avoid them in order to obtain accurate results.
Using incorrect coefficients:
One of the most common mistakes when calculating mole ratios is using incorrect coefficients from the balanced chemical equation. The coefficients represent the ratio of moles between reactants and products, and using incorrect coefficients can lead to inaccurate calculations. It is crucial to double-check the balanced equation and ensure that the coefficients are used correctly when calculating mole ratios.
Confusing reactants and products:
Another common mistake is confusing the reactants and products when setting up the mole ratio. It is easy to mistakenly use the moles of the product instead of the moles of the reactant, or vice versa. It is important to carefully identify the reactants and products and use the appropriate moles in the calculation.
Not converting units:
Conversions between units are often required when calculating mole ratios. For example, if the given information is in grams, it is necessary to convert to moles before performing the calculations. Failing to convert units properly can result in incorrect mole ratios. Always ensure that units are consistent throughout the calculation and make any necessary conversions before calculating the mole ratio.
Ignoring significant figures:
Lastly, it is important to consider significant figures when calculating mole ratios. Using too many or too few significant figures can introduce errors into the calculations. It is important to adhere to the rules of significant figures and round the final answer to the appropriate number of significant figures based on the given data.
By being aware of these common mistakes and taking steps to avoid them, students can improve their accuracy when calculating mole ratios. Double-checking coefficients, carefully identifying reactants and products, converting units properly, and considering significant figures are all crucial to obtaining reliable results in mole ratio calculations.
Tips and Tricks for Mastering Mole Ratio Calculations
Mole ratio calculations are an essential part of chemistry and can often be challenging for students. However, with the right tips and tricks, mastering mole ratio calculations can become much easier.
Understand the Concept
Before diving into calculations, it is crucial to have a strong understanding of the concept of mole ratio. Mole ratio represents the ratio between the number of moles of a substance in a chemical reaction. This ratio is derived from the balanced chemical equation.
Identify the Known and Unknown
When solving mole ratio problems, it is essential to identify what is known and what is unknown. This involves carefully reading the question and determining the given information and the information that needs to be calculated. By clearly identifying the known and unknown quantities, it becomes easier to set up the calculation.
Use the Stoichiometric Coefficients
The stoichiometric coefficients in a balanced chemical equation can be used as conversion factors to relate the moles of different substances involved in the reaction. By using these coefficients as mole ratios, one can convert between the known and unknown quantities. It is crucial to ensure that the coefficients are used correctly, with the known quantity in the denominator and the unknown quantity in the numerator.
Practice, Practice, Practice

Like any skill, mastering mole ratio calculations takes practice. By solving a variety of problems and working through different scenarios, you can reinforce your understanding of the concept and improve your problem-solving skills. Utilize practice problems, online resources, and textbooks to get ample practice and gain confidence in your abilities.
Check and Review
After completing a mole ratio calculation, it is always important to check your answer and review your steps. Double-checking your calculations helps to avoid errors and ensures the accuracy of your solution. Additionally, reviewing your approach to the problem can help identify areas for improvement and reinforce your understanding of the concept.
Mastering mole ratio calculations requires a combination of understanding the concept, practice, and attention to detail. By following these tips and tricks, you can tackle mole ratio problems with confidence and accuracy.