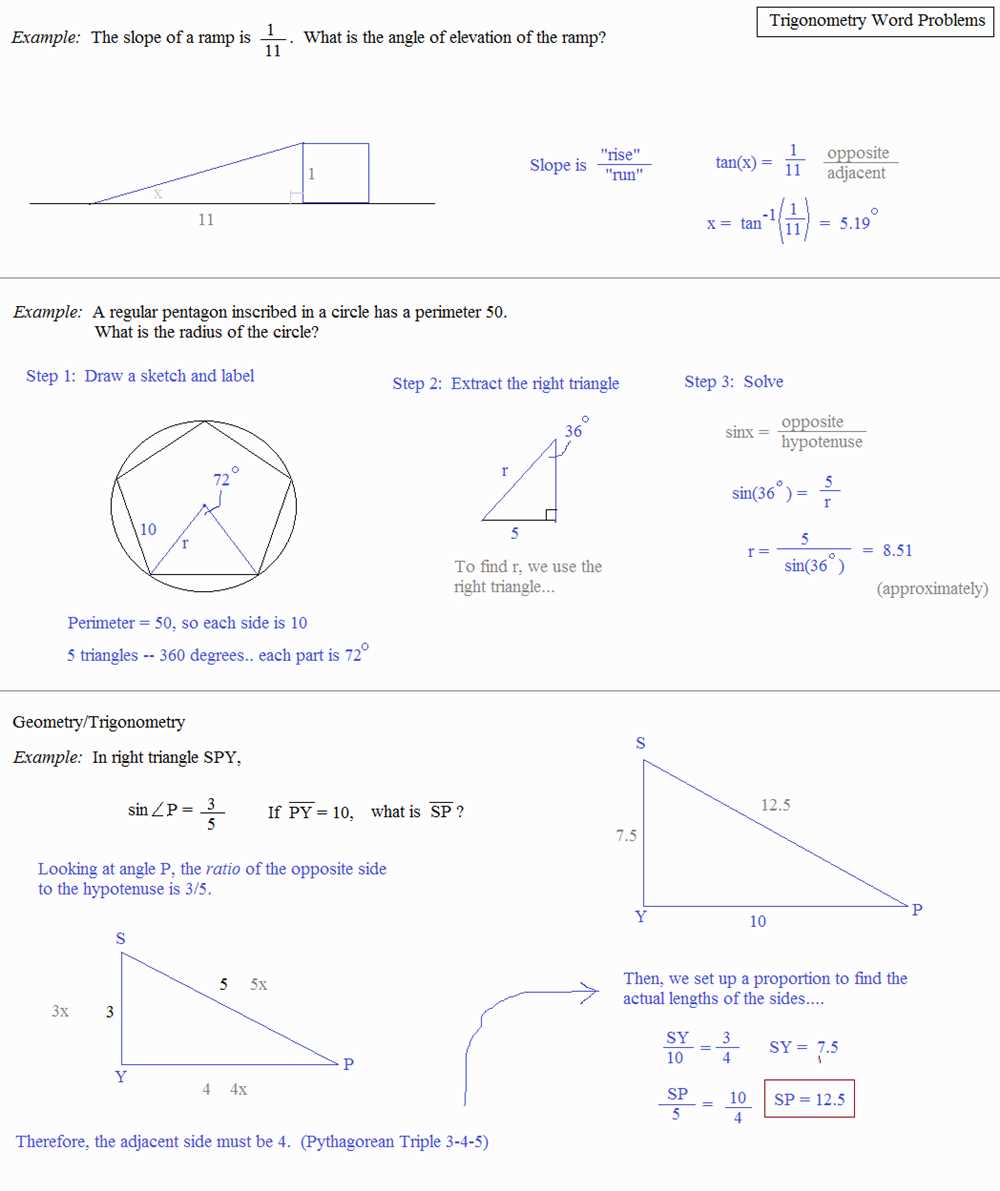
Oblique triangles are triangles with no right angle. They can often be found in real life situations, such as architecture, physics, and navigation. Solving problems involving oblique triangles requires the use of trigonometric ratios and the Pythagorean theorem.
One common type of problem involving oblique triangles is finding the length of one side given the lengths of the other two sides and the size of the included angle. For example, a problem might ask you to find the length of side ‘a’ in a triangle with side ‘b’ measuring 5 units, side ‘c’ measuring 7 units, and an included angle of 45 degrees.
Another type of problem involves finding the measures of the angles in an oblique triangle given the lengths of the three sides. These problems often require the use of the Law of Cosines or the Law of Sines. For example, a problem might ask you to find the measures of the three angles in a triangle with sides measuring 3 units, 4 units, and 5 units.
By familiarizing yourself with the different types of problems involving oblique triangles and practicing the appropriate trigonometric techniques, you will be better equipped to solve these types of problems. In this article, we will provide step-by-step solutions to various oblique triangle word problems to help you gain confidence and proficiency in solving them.
What are oblique triangles and how are they different from right triangles?
An oblique triangle is a type of triangle that does not have a right angle. Unlike a right triangle, which has one angle measuring 90 degrees, an oblique triangle has three acute angles or one obtuse angle. In other words, all the angles of an oblique triangle are less than 90 degrees or more than 90 degrees, but not exactly 90 degrees.
The absence of a right angle in an oblique triangle makes it different from a right triangle in several ways. Firstly, the Pythagorean theorem, which states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides, cannot be applied to oblique triangles. This means that oblique triangles require different methods and formulas to solve their problems.
Additionally, the trigonometric functions used to solve oblique triangles are different from those used in right triangles. In right triangles, we commonly use sine, cosine, and tangent functions. However, in oblique triangles, we also use the law of sines and the law of cosines, which are specific formulas designed to solve for the unknown sides and angles in these types of triangles.
Understanding the differences between oblique triangles and right triangles is crucial when solving oblique triangle word problems. By recognizing the absence of a right angle and applying the appropriate formulas and trigonometric functions, one can effectively solve problems related to oblique triangles.
What are word problems involving oblique triangles?
Word problems involving oblique triangles require the application of trigonometry to solve. In these problems, the given information typically includes two side lengths and an angle, or three side lengths of the triangle. The goal is to find the missing angle measures or side lengths using the given information and trigonometric ratios.
One common type of word problem involving oblique triangles is the “angle of depression” problem. In these problems, a person is observing an object, such as an airplane or a building, from a certain point on the ground. The given information includes the distance between the person and the object, as well as the angle of depression, which is the angle between the horizontal line from the person to the object and the person’s line of sight. The goal is to find the height or altitude of the object.
Another type of word problem involving oblique triangles is the “distance between two objects” problem. In these problems, two objects are observed from a certain point, and the given information includes the angles of elevation or depression between the observer and each object, as well as the distance between the two objects. The goal is to find the distance between the observer and each object.
These types of word problems require the use of trigonometric ratios such as sine, cosine, and tangent, as well as the Pythagorean theorem. By using these tools, the missing angle measures or side lengths of the oblique triangle can be determined.
Finding unknown side lengths in oblique triangles
An oblique triangle is a triangle that does not have a right angle. When given an oblique triangle, there may be cases where we need to find the lengths of the sides. To do this, we can use trigonometric ratios such as sine, cosine, and tangent.
One common scenario is when we know the lengths of two sides and the measure of an angle between them. In this case, we can use the Law of Cosines to find the length of the third side. The Law of Cosines states that in a triangle with sides a, b, and c, and angle C opposite side c:
- c^2 = a^2 + b^2 – 2ab * cos(C)
Another situation arises when we have the lengths of one side and two angles. In this case, we can use the Law of Sines to find the lengths of the other sides. The Law of Sines states that in a triangle with sides a, b, and c, and angles A, B, and C:
- a/sin(A) = b/sin(B) = c/sin(C)
If we know the lengths of all three sides, we can also use the Law of Cosines to find the measures of the angles in the triangle. By rearranging the equation, we can solve for each angle using the inverse cosine function.
In summary, finding unknown side lengths in oblique triangles involves using trigonometric ratios and the Laws of Cosines and Sines. These mathematical tools allow us to find missing side lengths and angles in a variety of given conditions. It is important to understand and apply these concepts in order to solve oblique triangle problems effectively.
Finding unknown angles in oblique triangles
Oblique triangles are triangles that have no right angles. In these types of triangles, it is often necessary to find the values of unknown angles in order to solve various problems. This can be done using the law of sines or the law of cosines, depending on the information given.
One common scenario is when we know the lengths of two sides and the measure of the included angle, but need to find the values of the other angles. In this case, we can use the law of cosines to find the unknown angles. The law of cosines states that the square of one side of a triangle is equal to the sum of the squares of the other two sides minus twice the product of those two sides and the cosine of the included angle.
Another situation is when we know the lengths of all three sides of the triangle, but need to find the measures of the angles. In this case, the law of cosines can still be used to find one angle, and then the law of sines can be used to find the remaining angles. The law of sines states that the ratio of the length of a side of a triangle to the sine of the opposite angle is the same for all three sides of the triangle.
- Example 1: Given that side a has a length of 5 units, side b has a length of 8 units, and the included angle is 60 degrees, we can use the law of cosines to find the value of angle C:
- Example 2: Given that side a has a length of 4 units, side b has a length of 6 units, and side c has a length of 7 units, we can use the law of cosines to find the value of angle C:
- Example 3: Given that side a has a length of 4 units, side b has a length of 6 units, and side c has a length of 7 units, we can use the law of sines to find the values of angles A and B:
a^2 = b^2 + c^2 – 2bc * cos(C)
c^2 = a^2 + b^2 – 2ab * cos(C)
sin(A) / a = sin(B) / b = sin(C) / c
In conclusion, finding unknown angles in oblique triangles can be achieved using the law of cosines or the law of sines, depending on the given information. These laws provide the necessary mathematical relationships to solve for the unknown angles and successfully complete various problems involving oblique triangles.
How to solve oblique triangle word problems?
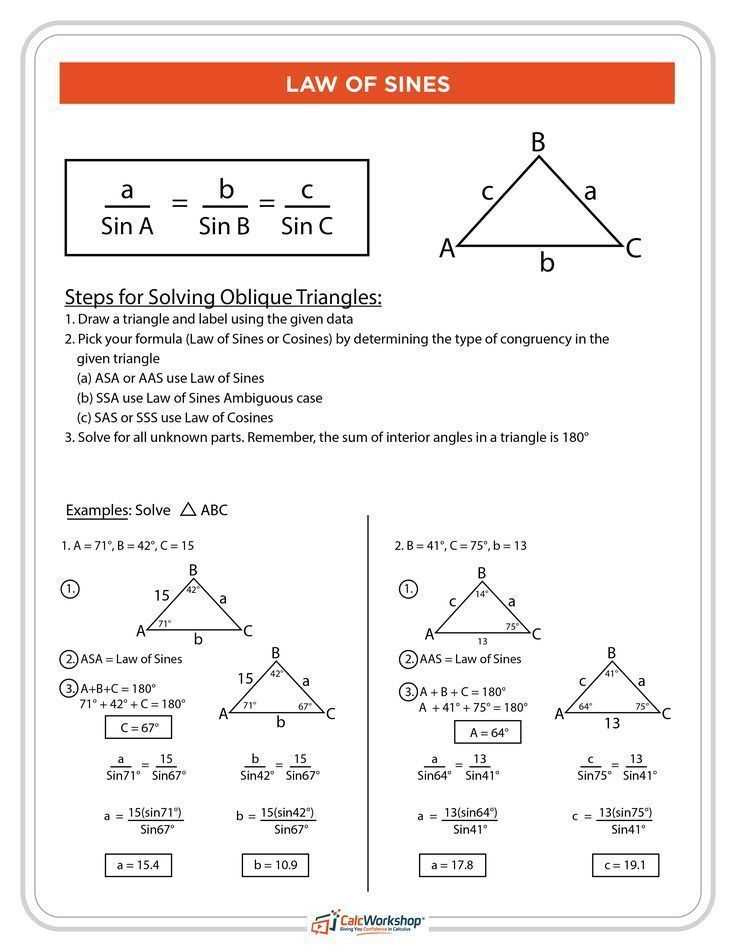
Oblique triangle word problems involve finding the measurements of angles and sides in a triangle where none of the angles are 90 degrees. These types of problems often require the use of trigonometry, specifically the sine, cosine, and tangent functions.
To solve oblique triangle word problems, follow these steps:
- Identify the given information: Read the problem carefully and identify what information is given. This may include side lengths, angles, or other relevant measurements.
- Draw a diagram: Create a diagram of the triangle and label the given information. This helps visualize the problem and makes it easier to set up equations.
- Use trigonometric functions: Determine which trigonometric function to use based on the given information. For example, if you’re given an angle and a side length, you can use the sine or cosine function to find another side length.
- Solve for missing sides or angles: Set up and solve the trigonometric equation to find the missing sides or angles of the triangle. Use appropriate units for angles (degrees or radians) based on the problem’s context.
- Check your answer: Once you’ve solved for the missing measurements, double-check your work to make sure it makes sense in the context of the problem. Ensure your answer is reasonable and matches the given information.
Using these steps, you can confidently solve oblique triangle word problems and find the missing measurements of angles and sides in the triangle.
Using the Law of Sines
The Law of Sines is a trigonometric formula that relates the sides and angles of any oblique triangle. It states that the ratio of the length of a side to the sine of its opposite angle is a constant value.
Let’s consider an example to better understand how to use the Law of Sines in oblique triangle problems. Suppose we have an oblique triangle with known side lengths a, b, and c, and unknown angles A, B, and C. To find the measure of one of the angles, we can use the Law of Sines.
The Law of Sines states that in a triangle with sides a, b, and c opposite angles A, B, and C respectively, the following relationship holds: sin(A)/a = sin(B)/b = sin(C)/c. This means that the ratio of the sine of an angle to the corresponding side length is constant for all three sides.
To find the measure of angle A, we can rearrange the formula as sin(A) = a*sin(B)/b. By substituting the known values of a and b, we can solve for sin(A) using a calculator. Taking the inverse sine of the resulting value, we can find the measure of angle A.
Similarly, we can use the Law of Sines to find the measures of angles B and C by rearranging the formula accordingly. Once we have obtained the measures of all three angles, we can use them to find any other unknown side lengths or angles in the oblique triangle using the Law of Cosines or other trigonometric formulas.
Using the Law of Cosines
In oblique triangles, where none of the angles are 90 degrees, the Law of Cosines can be used to calculate the lengths of the sides or the measures of the angles. The Law of Cosines states that the square of one side of a triangle is equal to the sum of the squares of the other two sides minus twice the product of the lengths of those sides multiplied by the cosine of the included angle.
Mathematically, the Law of Cosines can be written as:
c^2 = a^2 + b^2 – 2ab*cos(C)
Where c represents the side opposite to angle C, and a and b represent the other two sides of the triangle.
To solve a triangle using the Law of Cosines, you need to have at least three known values, including one side and two angles, or two sides and one angle. Using the equation, you can then solve for the unknown side or angle by rearranging the equation and applying the appropriate trigonometric functions.
For example, let’s say we have a triangle with side a = 8, side b = 10, and angle C = 45 degrees. To find the length of side c, we can use the Law of Cosines as follows:
| c^2 | = | a^2 + b^2 – 2ab*cos(C) |
|---|---|---|
| c^2 | = | 8^2 + 10^2 – 2*8*10*cos(45) |
| c^2 | = | 64 + 100 – 160*cos(45) |
| c^2 | = | 164 – 160*0.7071 |
| c^2 | = | 164 – 113.1376 |
| c^2 | = | 50.8624 |
| c | = | sqrt(50.8624) |
| c | = | 7.13 |
Therefore, the length of side c is approximately 7.13. The Law of Cosines allows us to solve for the unknown side in an oblique triangle using given side lengths and angles.
Examples of Oblique Triangle Word Problems with Step-by-Step Solutions
Oblique triangles are triangles that do not have a right angle. These types of triangles can present interesting word problems that require careful analysis and application of trigonometric principles to find their solutions. Here are a few examples of oblique triangle word problems, along with step-by-step solutions.
Example 1
A plane is flying at an altitude of 10,000 feet. From a point on the ground, the angle of elevation to the plane is measured to be 60 degrees. Find the distance between the plane and the point on the ground.
Solution:
- Let x be the distance between the plane and the point on the ground.
- By drawing a right triangle with the plane, the point on the ground, and the altitude as its sides, we can see that the angle opposite the side x is 60 degrees.
- Using the sine function, we can set up the equation sin(60) = 10,000 / x.
- Simplifying the equation, we get x = 10,000 / sin(60).
- Using a calculator, we find that sin(60) is approximately 0.866, so x = 10,000 / 0.866.
- Calculating this further, we get x ≈ 11,547.05 feet.
Example 2

A ship is sailing due east for 8 miles. Then it changes course and sails northwest for 6 miles. What is the distance between its starting point and its current position?
Solution:
- By drawing a right triangle with the ship’s starting point, the current position, and the distance sailed as its sides, we can see that the angle between the north direction and the line connecting the starting point and the current position is 45 degrees.
- Since the ship traveled 8 miles due east and 6 miles in a northwest direction, the horizontal side of the right triangle is 8 + 6 = 14 miles.
- Using the Pythagorean theorem, we can find the distance between the starting point and the current position, which is the hypotenuse of the right triangle.
- The equation becomes c^2 = 8^2 + 6^2, where c is the length of the hypotenuse.
- Calculating this further, we get c^2 = 64 + 36, so c^2 = 100.
- Taking the square root of both sides, we find that c = 10 miles.
These examples demonstrate how oblique triangle word problems can be solved using trigonometric principles such as sine, cosine, and the Pythagorean theorem. By carefully analyzing the given information and applying the appropriate formulas, the solutions to these types of problems can be found step-by-step.