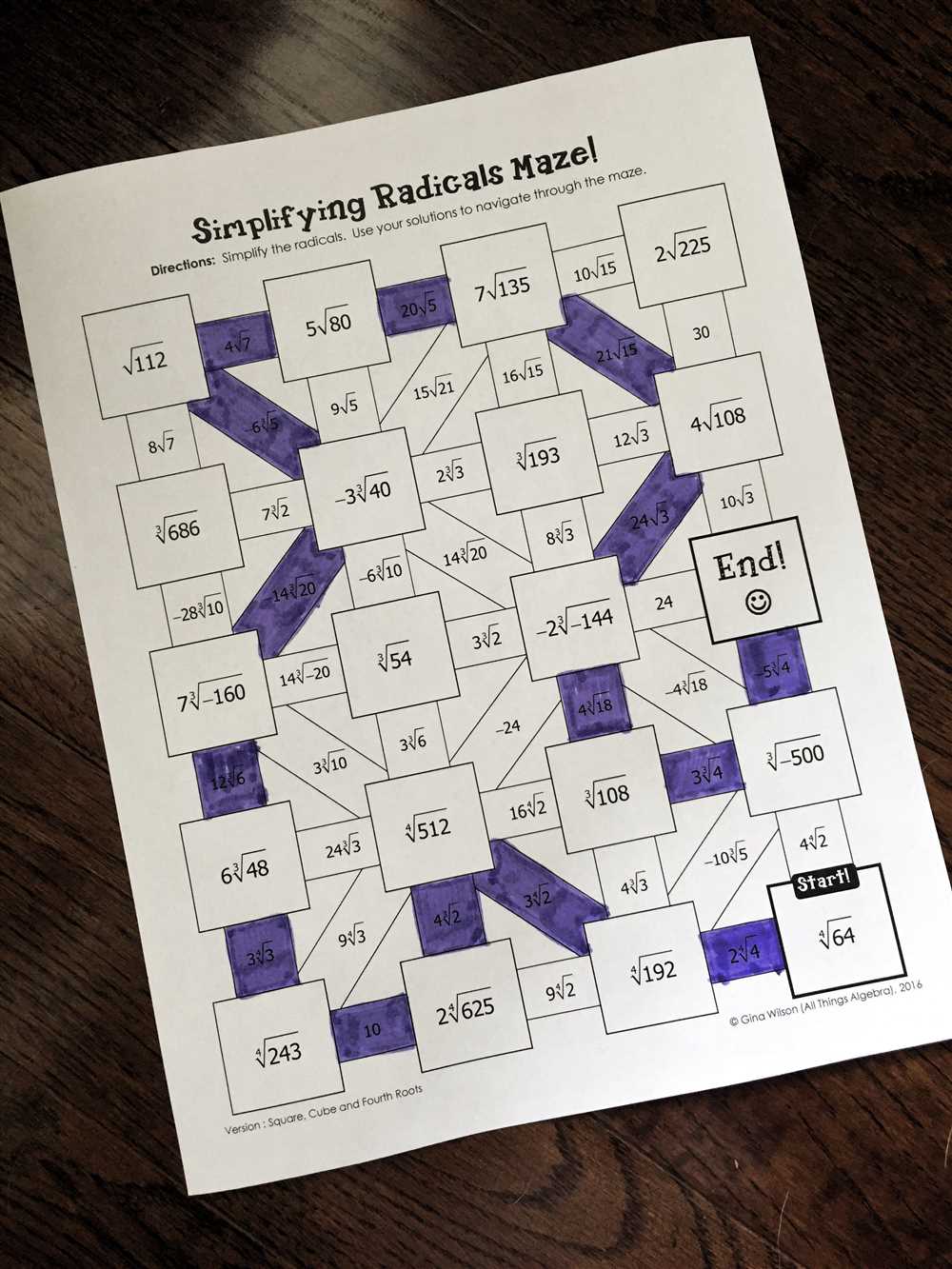
When it comes to understanding and solving operations of functions, having an answer key can be incredibly helpful. In this article, we will explore the operations of functions maze answer key, which provides step-by-step solutions to different types of function problems.
The operations of functions maze answer key is designed to guide students through solving complex function problems with ease. It breaks down the process into manageable steps, making it easier for students to understand and apply the concepts. With the help of this answer key, students can check their work and identify any mistakes they may have made.
From simplifying expressions to evaluating composite functions, the operations of functions maze answer key covers a wide range of topics. It provides clear explanations and examples to help students grasp the underlying concepts and apply them to different situations. Whether you are a beginner or an advanced learner, this answer key can be a valuable tool in your journey to mastering operations of functions.
In conclusion, the operations of functions maze answer key is an essential resource for students studying functions. It offers a comprehensive guide to solving various function problems and helps students develop their problem-solving skills. With its step-by-step solutions and clear explanations, this answer key will undoubtedly be a valuable companion for any student navigating the world of operations of functions.
Operations of Functions Maze Answer Key: Explained and Simplified
In the topic of mathematics, functions play a crucial role in understanding relationships between variables and their corresponding outputs. One common exercise that helps reinforce this concept is the “Operations of Functions Maze.” This maze consists of a series of mathematical operations that students must navigate through to find the correct path.
The Operations of Functions Maze provides students with valuable practice in performing various operations on functions, including addition, subtraction, multiplication, division, composition, and inverse functions. The maze represents a sequence of steps that students must follow, using their knowledge of these operations, to arrive at the correct answer.
The answer key for the Operations of Functions Maze serves as a guide for students to check their work and ensure that they have correctly followed the given operations. It provides step-by-step explanations and solutions for each operation, helping students understand the reasoning behind each step.
The answer key begins by outlining the initial function or functions provided in the maze. It then breaks down each individual operation, clearly indicating the operation being performed and the resulting function. This step-by-step approach helps students identify where they may have made a mistake and allows them to correct it.
By using the Operations of Functions Maze Answer Key, students can gain a deeper understanding of the operations involved in functions and improve their problem-solving skills. It serves as a valuable tool for self-assessment, allowing students to identify areas where they may need additional practice or clarification.
Overall, the Operations of Functions Maze Answer Key provides a clear and concise explanation of the steps involved in solving the maze. It is an excellent resource for students to enhance their understanding of functions and strengthen their mathematical abilities.
Understanding Operations of Functions
The operations of functions play a crucial role in mathematics and help us understand how functions can be manipulated and combined. By performing operations on functions, we can create new functions that can exhibit different properties than the original functions.
Function composition is one of the fundamental operations of functions, which involves combining two functions to create a new function. It is denoted by the symbol “∘”. When we compose two functions f and g, the result is a new function h(x), where h(x) = f(g(x)). This means that the output of g(x) is fed into f(x) as an input. The concept of function composition allows us to analyze complex functions by breaking them down into simpler components.
Function addition is another operation that can be performed on functions. When we add two functions f and g, the result is a new function h(x), where h(x) = f(x) + g(x). This operation is similar to arithmetic addition, where we add the corresponding values of f(x) and g(x) to obtain the value of h(x) at each point.
Function multiplication is yet another operation that can be applied to functions. When we multiply two functions f and g, the result is a new function h(x), where h(x) = f(x) * g(x). This operation is analogous to arithmetic multiplication, where we multiply the corresponding values of f(x) and g(x) to obtain the value of h(x) at each point.
In addition to these basic operations, there are various other operations that can be performed on functions, such as subtraction, division, and exponentiation. Each of these operations manipulates the functions in a different way and yields different results.
Understanding the operations of functions is essential in many areas of mathematics, including calculus, algebra, and mathematical modeling. By mastering these operations, we can analyze and manipulate functions to solve complex mathematical problems and gain a deeper insight into the behavior of various mathematical phenomena.
Key Concepts in Operations of Functions Maze
Operations of functions involve performing mathematical operations such as addition, subtraction, multiplication, and division on functions. These operations can help manipulate and combine functions to create new functions or analyze their properties.
Some key concepts in operations of functions include:
- Function composition: This involves combining two or more functions by substituting the output of one function into another. The resulting function represents the composition of the functions.
- Domain and range: The domain of a function refers to the set of all possible input values, while the range refers to the set of all possible output values. When performing operations on functions, it is important to consider the domains and ranges of the functions involved.
- Addition and subtraction of functions: By adding or subtracting functions, you can create new functions that represent the sum or difference of the original functions at each point in their domains.
- Multiplication and division of functions: Multiplying or dividing functions can also result in new functions. The new function represents the product or quotient of the original functions at each point in their domains.
- Transformation of functions: Operations of functions can also involve transforming the original function by shifting it horizontally, vertically, stretching or compressing it, or reflecting it.
By understanding these key concepts, you can effectively navigate and solve operations of functions mazes, and more importantly, apply these concepts to real-world problems involving functions and mathematical modeling.
How to Solve the Operations of Functions Maze
Solving the Operations of Functions Maze requires a good understanding of how functions work and how to perform operations with them. Here are some key steps to successfully navigate through the maze.
1. Identify the given functions
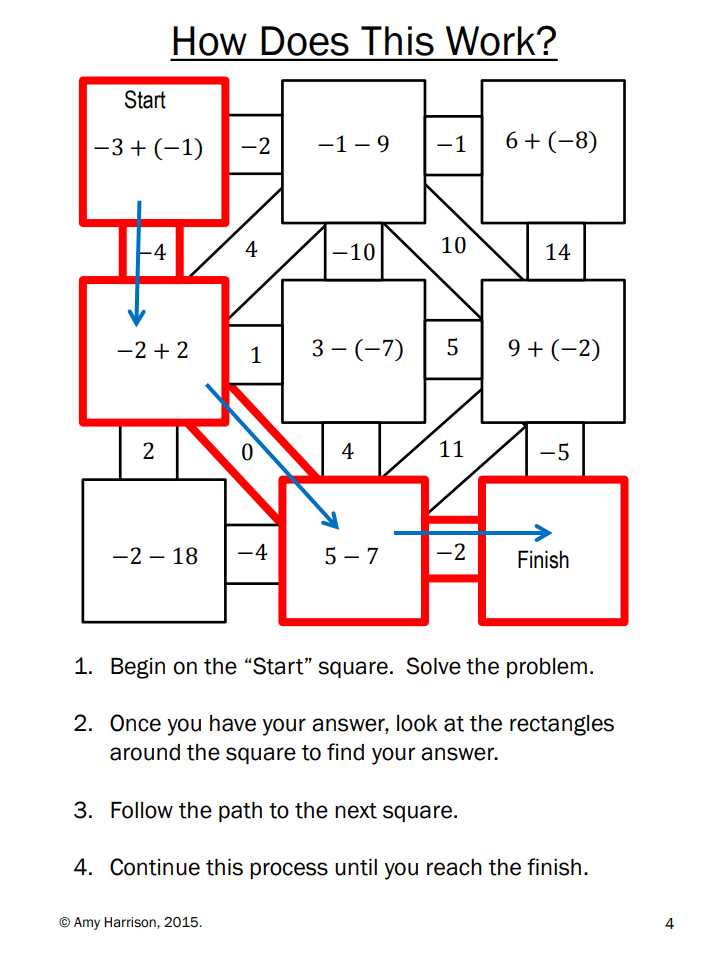
Start by identifying the functions that are given in the maze. These functions may be represented by equations or given in a verbal form. Make a note of each function and its corresponding variables.
2. Determine the operations
Next, determine the operations that need to be performed on the given functions. These operations could be addition, subtraction, multiplication, division, or composition of functions. Understand the rules and properties of these operations and how they affect functions.
3. Simplify the expressions
Use the rules of algebra to simplify the expressions in each step of the maze. Combine like terms, perform any necessary calculations, and simplify as much as possible. This will help to make the steps more manageable and easier to follow.
4. Follow the instructions
Read the instructions for each step carefully. They will guide you through the maze and tell you what operation to perform on which function. Be sure to follow the instructions accurately to avoid getting lost or making mistakes.
5. Keep track of your progress
As you navigate through the maze, keep track of your progress by marking off the steps you have completed. This will help you stay organized and ensure that you don’t miss any steps or make any errors.
By following these steps and staying focused, you will be able to successfully solve the Operations of Functions Maze and find the correct answer. Remember to take your time and double-check your work to ensure accuracy.
Step-by-Step Walkthrough of the Operations of Functions Maze
When solving a maze that involves the operations of functions, it is important to understand the concept of functions and how they are manipulated. Functions are mathematical relationships that take an input and produce an output. In this maze, you will encounter four different operations: addition, subtraction, multiplication, and division.
To successfully navigate the maze, you must follow the rules for each operation. For addition, you will need to add the values of the function and the given input. For subtraction, you subtract the value of the function from the input. For multiplication, you multiply the function value and the input. And for division, you divide the input by the function value.
Each operation will lead you to a different path in the maze. As you make your way through the maze, it is important to keep track of the operations you have performed and the results you have obtained. This will help you determine the correct path to take. You can use a table to organize your calculations and make it easier to see the relationship between the inputs and outputs.
When you reach the end of the maze, you should have a final output value. This value represents the result of applying all the operations to the initial input. It is important to check your final answer to ensure accuracy. You can do this by following the path backwards and applying the inverse of each operation to the final output. If you end up with the initial input, then your answer is correct.
Overall, navigating the operations of functions maze requires a strong understanding of the four basic operations and how they are applied to functions. By carefully following the rules and keeping track of your calculations, you can successfully navigate the maze and find the correct answer.
Common Mistakes to Avoid in the Operations of Functions Maze
When navigating through the Operations of Functions Maze, students may encounter some common mistakes that can hinder their progress. It is important to be aware of these mistakes in order to successfully complete the maze and understand the operations of functions correctly.
1. Forgetting to Apply the Correct Operation
One common mistake is forgetting to apply the correct operation when performing operations on functions. For example, adding two functions requires adding the corresponding terms in each function, not simply adding the functions as a whole. Students should carefully read the instructions and pay attention to the specific operation that needs to be applied.
2. Not Simplifying the Resulting Function
Another mistake is failing to simplify the resulting function after performing an operation. The goal of the maze is to simplify the functions as much as possible. Students should simplify the resulting function by combining like terms, canceling out common factors, or applying any other simplification techniques that may be applicable.
3. Overlooking Restrictions on the Domain and Range
It is crucial to pay attention to any given restrictions on the domain and range of the functions. Ignoring these restrictions can lead to incorrect solutions. Students should carefully consider whether the resulting function satisfies the given restrictions and make any necessary adjustments.
To successfully navigate through the Operations of Functions Maze, students should avoid these common mistakes by applying the correct operations, simplifying the resulting function, and considering any restrictions on the domain and range. By doing so, they will be able to efficiently solve the maze and deepen their understanding of operations on functions.
Tips and Tricks for Success in Operations of Functions Mazes
1. Understand function operations: Before attempting an operations of functions maze, it is important to have a clear understanding of how different operations alter functions. Familiarize yourself with operations such as addition, subtraction, multiplication, division, composition, and inverse functions. Make sure you can confidently apply these operations to functions.
2. Start with simple mazes: If you are new to operations of functions mazes, it is helpful to begin with simpler mazes. These mazes typically involve basic operations like addition and subtraction. As you become more comfortable, you can progress to more complex mazes that involve multiple operations.
3. Pay attention to function notation: Function notation is crucial in operations of functions mazes. Make sure you understand how to interpret and manipulate function notation. This includes understanding how to identify the input and output variables, and how to substitute values into functions.
4. Work step by step: When solving an operations of functions maze, it can be overwhelming to look at the entire maze at once. Break the problem down into smaller steps and tackle them one by one. Start by applying the first operation, then move on to the next, and so on. This approach helps to prevent confusion and mistakes.
5. Check your answers: After completing a operations of functions maze, always double-check your answers. Be sure to substitute your answers back into the original functions to ensure they are correct. Mistakes can easily occur, especially when dealing with multiple operations, so it is important to verify your work.
By following these tips and tricks, you can improve your success in operations of functions mazes. Practice regularly to strengthen your understanding of function operations and get faster at solving these types of problems.