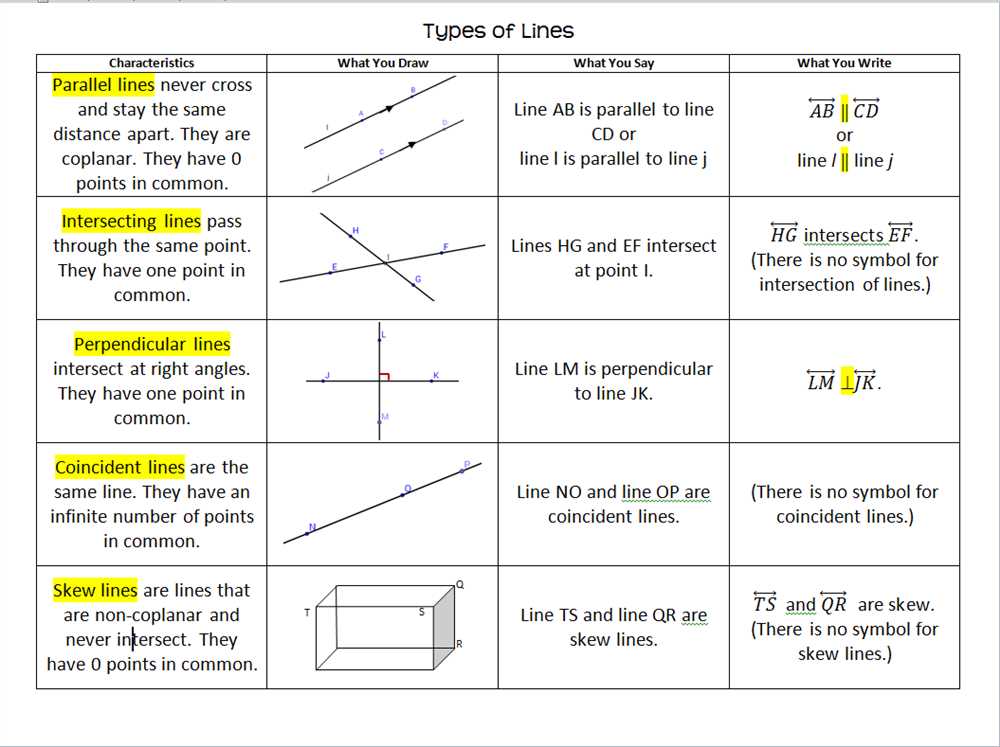
In mathematics, the study of lines is an important topic that helps us understand the relationships between different shapes and figures. One of the key concepts in this area is parallel and perpendicular lines. Parallel lines are two lines that are always the same distance apart and will never intersect, while perpendicular lines are two lines that intersect at a right angle.
A unit test on parallel and perpendicular lines is a comprehensive assessment that evaluates a student’s understanding of these concepts. It covers topics such as identifying parallel and perpendicular lines, determining the equations of parallel and perpendicular lines, and solving problems involving these types of lines. The test may include multiple-choice questions, short answer questions, and problem-solving tasks.
Successfully completing a parallel and perpendicular lines unit test requires a solid understanding of the basic properties and characteristics of these lines. Students should be able to identify parallel and perpendicular lines in various geometric figures, as well as understand the equations that represent these lines. They should also be able to apply this knowledge to solve real-world problems that involve parallel and perpendicular lines.
Overall, a parallel and perpendicular lines unit test is an important assessment tool that measures a student’s proficiency in understanding and applying the concepts and properties of parallel and perpendicular lines. It helps educators assess the effectiveness of their teaching and provides students with an opportunity to demonstrate their knowledge and skills in this area of mathematics.
Parallel and Perpendicular Lines Unit Test
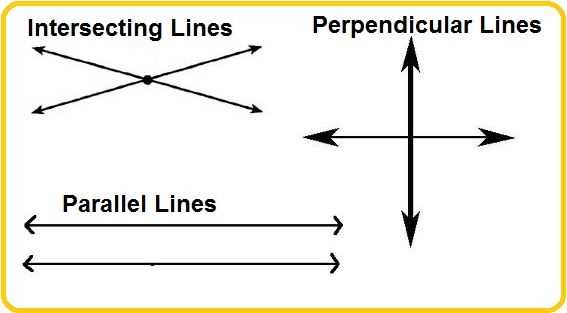
Are you ready to test your knowledge of parallel and perpendicular lines? This unit test will evaluate your understanding of these important concepts in geometry. Make sure you have reviewed the material thoroughly before starting the test.
The test will assess your ability to identify parallel and perpendicular lines, find the slope of a line, determine if lines are parallel or perpendicular based on their equations or graphs, and solve problems involving parallel and perpendicular lines. You will be asked to apply your knowledge in various scenarios to demonstrate your understanding.
- Identifying Parallel and Perpendicular Lines: You will be given multiple line pairs and asked to determine if they are parallel, perpendicular, or neither.
- Finding the Slope of a Line: You may encounter questions that require you to calculate the slope of a line using its equation or two given points on the line.
- Determining Parallel or Perpendicular Lines: You will be asked to analyze equations or graphs and determine if the lines are parallel or perpendicular.
- Solving Problems: The test may include word problems that involve parallel and perpendicular lines. You will need to apply your knowledge to solve these problems and provide the correct solution.
Remember to show all your work and provide clear explanations for your answers. Double-check your calculations and be sure to answer each question to the best of your ability. Good luck!
Understanding Parallel Lines
Parallel lines are two lines in a plane that never intersect. They have the same slope and are always equidistant from each other. Parallel lines have a special property that enables us to analyze and solve various geometric problems.
In geometry, the slope-intercept form of a line equation is often used to determine whether two lines are parallel. Parallel lines have the same slope, which means that their lines have the same steepness and direction. For example, the equation of a line with a slope of 2 and a y-intercept of 3 is y = 2x + 3. Any other line with the equation y = 2x + c, where c is a constant, will be parallel to the first line.
In addition to their mathematical properties, parallel lines have important applications in daily life. For example, parallel lines can be found in road design, where the lanes on a highway are parallel to each other. This ensures that vehicles can smoothly and safely travel in their respective lanes without intersecting. Similarly, parallel train tracks are essential for trains to travel safely without colliding with each other.
In conclusion, understanding parallel lines is crucial in geometry and has real-life implications. When lines are parallel, they never intersect and have the same slope. This concept is essential for solving geometric problems and is also essential for practical applications, such as road and railway design.
Identifying Parallel Lines
Parallel lines are a fundamental concept in geometry. They are lines that never intersect, no matter how far they extend. In order to identify parallel lines, we need to consider two important criteria: their slopes and their y-intercepts.
Slope: The slope of a line represents its steepness. If two lines have the same slope, they are parallel. To find the slope of a line, we can use the formula: slope = (change in y) / (change in x). If the slopes of two lines are equal, then they are parallel.
Y-intercept: The y-intercept is the point where the line intersects the y-axis. If two lines have the same y-intercept, they are parallel. To find the y-intercept of a line, we look at the point where the line crosses the y-axis.
By examining the slopes and y-intercepts of two lines, we can determine whether they are parallel or not. If the slopes are equal and the y-intercepts are different, the lines are parallel. If the slopes are different, the lines are not parallel. Additionally, if the slopes are equal and the y-intercepts are equal, the lines are not parallel but they are coincident or overlapping.
Properties of Parallel Lines
Parallel lines are a fundamental concept in geometry, and they possess several important properties. When two lines are parallel, they never intersect. This means that they have the same slope. If two lines have different slopes, they are not parallel. Conversely, if two lines have the same slope, they are either coincident (i.e., they lie on top of each other) or parallel. The slopes of parallel lines are equal, but their y-intercepts can be different.
One property of parallel lines is that the alternate interior angles are congruent. Alternate interior angles are pairs of angles that are on opposite sides of a transversal and are on the inside of the two parallel lines. So, if two lines are parallel, the alternate interior angles formed by a transversal cutting through them will be equal. This property is useful in solving problems involving angles formed by parallel lines.
Another property of parallel lines is that the corresponding angles are congruent. Corresponding angles are pairs of angles that are in the same position relative to the two parallel lines and the transversal that cuts through them. For example, if two lines are cut by a transversal and form a pair of corresponding angles, then those angles will be equal. This property allows for the calculation of unknown angles in geometric figures involving parallel lines.
In addition, parallel lines have the property that the consecutive interior angles are supplementary. Consecutive interior angles are pairs of angles that are on the same side of the transversal and are on the inside of the two parallel lines. In other words, they are adjacent angles formed by alternate interior angles. If two lines are parallel, then the consecutive interior angles formed by a transversal cutting through them will add up to 180 degrees.
In summary, parallel lines have the same slope, their alternate interior angles are congruent, their corresponding angles are congruent, and their consecutive interior angles are supplementary. These properties are fundamental for understanding and solving problems involving parallel lines in geometry.
Solving Problems with Parallel Lines
Parallel lines are lines that never intersect, no matter how far they are extended. When working with parallel lines, there are a few key properties and relationships to keep in mind. One important property is that corresponding angles formed by a transversal cutting through parallel lines are congruent. This means that if two lines are parallel and a third line intersects them, the angles that are in the same position relative to the transversal will have the same measure.
Using this property, we can solve various problems involving parallel lines. For example, if we are given a diagram with parallel lines and a transversal, we can find the measure of an unknown angle by identifying corresponding angles. Similarly, if we are given the measure of an angle in a diagram, we can determine if the lines are parallel by checking if the corresponding angles have the same measure.
Another important relationship involving parallel lines is the alternate interior angles theorem. According to this theorem, if two parallel lines are intersected by a transversal, then the alternate interior angles are congruent. This means that if a transversal intersects two lines and two interior angles are on opposite sides of the transversal and between the two lines, they will have the same measure.
To solve problems involving alternate interior angles, we can use the theorem to determine the measure of an unknown angle. Additionally, we can use this relationship to prove that lines are parallel if the alternate interior angles are congruent.
Identifying Perpendicular Lines
Perpendicular lines are lines that intersect at a right angle, forming a 90-degree angle between them. They have a special relationship and can be identified by certain characteristics.
One way to identify perpendicular lines is by looking at their slopes. In Euclidean geometry, the slope of a line is a measure of its steepness. If two lines are perpendicular, then their slopes are negative reciprocals of each other. This means that if the slope of one line is m, the slope of the perpendicular line is -1/m.
For example:
- If a line has a slope of 2, its perpendicular line will have a slope of -1/2.
- If a line has a slope of -3/4, its perpendicular line will have a slope of 4/3.
Another way to identify perpendicular lines is by examining their equations. In the coordinate plane, lines can be represented by linear equations in the form y = mx + b, where m is the slope and b is the y-intercept. If two lines have slopes that are negative reciprocals of each other and they intersect at a point, then they are perpendicular.
For example:
- The line y = 2x + 3 is perpendicular to the line y = -1/2x + 4 because their slopes are negative reciprocals of each other.
- The line y = 5x + 2 is not perpendicular to the line y = 3x + 1 because their slopes are not negative reciprocals of each other.
In summary, perpendicular lines can be identified by their slopes and equations. They intersect at a right angle and their slopes are negative reciprocals of each other. Understanding these characteristics can help in identifying and working with perpendicular lines in various mathematical problems and applications.
Properties of Perpendicular Lines

The concept of perpendicular lines is an important one in geometry. Perpendicular lines are two lines that intersect at a right angle, forming a 90-degree angle. This intersection point is called the point of perpendicularity. When two lines are perpendicular, they have several unique properties that can be observed and used in various mathematical and real-world situations.
1. Intersect at a right angle: The most fundamental property of perpendicular lines is that they intersect at a right angle. This means that the measure of the angles formed at the point of perpendicularity is always 90 degrees. This property is used extensively in geometry to determine the relationships between angles and to solve geometric problems.
2. Opposite slopes: Another property of perpendicular lines is that their slopes are negative reciprocals of each other. In other words, the slope of one line is the negative inverse of the slope of the other line. This relationship can be expressed mathematically as m1 = -1/m2, where m1 and m2 are the slopes of the two perpendicular lines. This property is often used to determine if two lines are perpendicular to each other.
3. Unique segment relationships: Perpendicular lines have several unique segment relationships. One such relationship is that the line segments formed by the point of perpendicularity are congruent to each other. Additionally, if a line is perpendicular to one of two parallel lines, it is also perpendicular to the other parallel line. These segment relationships are useful in solving problems involving perpendicular lines in real-world scenarios.
4. Orthogonal axes: Perpendicular lines are commonly used to create orthogonal axes in coordinate geometry. The x-axis and y-axis on a coordinate plane are perpendicular to each other, forming four quadrants. This allows for easy plotting and analysis of points and equations in a two-dimensional space. The concept of perpendicular lines is also extended to three-dimensional space, where three mutually perpendicular axes are used.
5. Used in construction and architecture: Perpendicular lines are widely used in construction and architecture. They are used to create right angles, ensuring structures are square and stable. Perpendicular lines are also used to layout foundations, walls, and other structural elements, ensuring accuracy in the construction process. Architects and engineers rely on the properties of perpendicular lines to create sturdy and functional designs.
- Perpendicular lines intersect at a right angle.
- The slopes of perpendicular lines are negative reciprocals of each other.
- The line segments formed by the point of perpendicularity are congruent to each other.
- Perpendicular lines are commonly used to create orthogonal axes in coordinate geometry.
- Perpendicular lines are widely used in construction and architecture to create right angles and ensure structural stability.
Solving Problems with Perpendicular Lines
Perpendicular lines are lines that intersect at a right angle. They have slopes that are negative reciprocals of each other. When solving problems involving perpendicular lines, it is important to understand their properties and how to use them effectively.
One common problem involving perpendicular lines is finding the equation of a line that is perpendicular to a given line and passes through a specific point. To solve this problem, we can start by finding the slope of the given line. Then, we can determine the negative reciprocal of that slope to find the slope of the perpendicular line. Finally, we can use the point-slope form of a line to plug in the coordinates of the given point and the slope of the perpendicular line to find the equation.
Another problem involving perpendicular lines is determining whether two given lines are perpendicular to each other. To solve this problem, we can compare the slopes of the two lines. If the slopes are negative reciprocals of each other, then the lines are perpendicular. If the slopes are equal, then the lines are parallel or coincident. By using the concept of slope and knowing the property of perpendicular lines, we can easily determine the relationship between two given lines.
In summary, solving problems with perpendicular lines involves understanding their properties, finding the negative reciprocal of a given slope, and using various forms of equations to find the relationship between lines. By applying these concepts, we can solve problems related to perpendicular lines and gain a deeper understanding of their geometric properties.