
Understanding the relationships between parallel lines and transversals is key to solving missing angle problems. In this maze activity, students are challenged to find the missing angles by applying their knowledge of parallel lines and transversals. This answer key provides a step-by-step solution to the maze, helping students check their work and gain a deeper understanding of these geometric concepts.
The maze is designed with various angle pairs formed by parallel lines and a transversal. Each angle in the maze has a corresponding angle that is congruent or supplementary to it. To solve the maze, students need to identify these angle pairs and determine the missing angle by using the properties of parallel lines and transversals.
The answer key walks through the maze, highlighting each angle pair and explaining the steps to find the missing angle. It serves as a valuable resource for teachers and students alike, providing a clear and logical solution to the maze. By following the answer key, students can verify their own answers, identify any mistakes, and gain a better understanding of the concepts involved.
Parallel Lines and Transversals: Explained
Parallel lines and transversals are fundamental concepts in geometry that involve the intersection of two or more lines. Understanding these concepts is crucial for solving a variety of geometric problems and proving theorems.
A transversal is a line that intersects two or more other lines. When a transversal intersects a pair of parallel lines, several important relationships and properties arise.
One of the most fundamental properties is that corresponding angles are congruent. Corresponding angles are angles that are in the same relative position at each intersection. For example, if a transversal intersects two parallel lines and forms an angle on the top left corner, the corresponding angle on the bottom right corner will be congruent. This property can be extended to other pairs of corresponding angles formed by the transversal.
Another important property is that alternate interior angles are congruent. Alternate interior angles are angles that are on opposite sides of the transversal and inside the parallel lines. For example, if a transversal intersects two parallel lines and forms an angle on the top left corner, the alternate interior angle on the top right corner will be congruent.
These properties, along with others such as alternate exterior angles and consecutive interior angles, allow us to solve problems involving parallel lines and transversals. They also serve as the foundation for proving more complex theorems related to geometry.
By understanding and applying the properties of parallel lines and transversals, we can solve missing angle mazes and other geometric puzzles. These concepts are not only important for geometry class but also have real-world applications, such as in architecture and engineering.
What are Parallel Lines and Transversals?
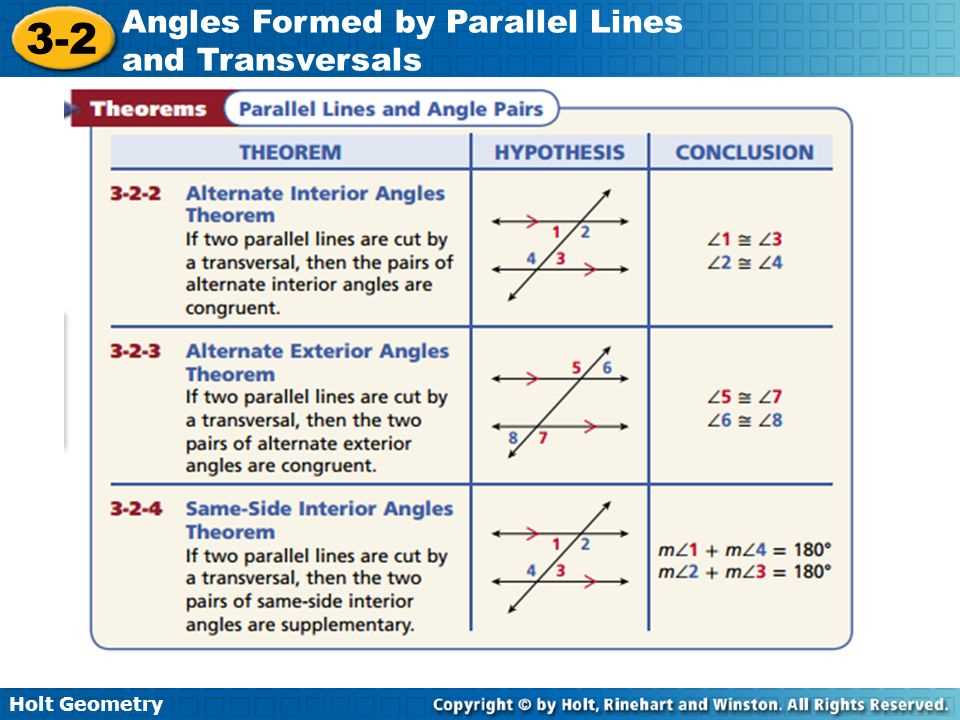
Parallel lines and transversals are fundamental concepts in geometry. Parallel lines are lines that never intersect, no matter how far they are extended. Transversals are lines that intersect two or more other lines at different points. When a transversal intersects two parallel lines, various angle relationships are formed.
One of the most important angle relationships formed by parallel lines and transversals is the corresponding angles. Corresponding angles are pairs of angles that are in the same position relative to the parallel lines and transversal. In other words, they are in the same location on each side of the transversal and on the same line of sight with the parallel lines. Corresponding angles are congruent, which means they have the same measure.
Another angle relationship formed by parallel lines and transversals is the alternate interior angles. Alternate interior angles are pairs of angles that are on opposite sides of the transversal and inside the parallel lines. They are congruent and have the same measure as well.
Parallel lines and transversals have many other angle relationships, such as alternate exterior angles, consecutive interior angles, and vertical angles. Understanding these angle relationships is crucial in solving problems and proving theorems related to parallel lines and transversals.
Properties and Relationships of Parallel Lines and Transversals

When studying parallel lines and transversals, it is important to understand the properties and relationships that exist between these lines. Parallel lines are lines that never intersect and are always equidistant from each other. They have the same slope and will never cross no matter how long they extend.
A transversal is a line that intersects two or more parallel lines. It creates several angles between the intersected lines, which can be classified based on their relationships.
Corresponding angles: When a transversal intersects two parallel lines, corresponding angles are formed on the same side of the transversal and in the same relative position. These angles are congruent or equal in measure.
Alternate interior angles: When a transversal intersects two parallel lines, alternate interior angles are formed on the inside of the parallel lines and on opposite sides of the transversal. These angles are congruent or equal in measure.
Alternate exterior angles: When a transversal intersects two parallel lines, alternate exterior angles are formed on the outside of the parallel lines and on opposite sides of the transversal. These angles are congruent or equal in measure.
Same-side interior angles: When a transversal intersects two parallel lines, same-side interior angles are formed on the inside of the parallel lines and on the same side of the transversal. These angles are supplementary, meaning their measures add up to 180 degrees.
Vertical angles: When two lines intersect, they form two pairs of vertical angles. Vertical angles are congruent or equal in measure.
By understanding these properties and relationships, one can solve various problems involving parallel lines and transversals, such as finding missing angles or proving statements about geometric figures. It is important to apply these concepts in real-world scenarios, such as architectural design or navigation, where parallel lines and transversals play a significant role.
Missing Angle Maze: An Engaging Activity
The Missing Angle Maze is a fun and interactive activity that helps students practice their understanding of parallel lines and transversals. This activity is designed to engage students and make learning about angles enjoyable and interactive. By working their way through the maze, students will have the opportunity to apply their knowledge of angle relationships and find missing angles.
One of the key features of the Missing Angle Maze is its visual appeal. The maze is designed with vibrant colors and eye-catching graphics to make it visually appealing for students. This not only helps to capture their attention but also makes the activity more enjoyable. The engaging visuals help students stay motivated and focused, ensuring that they are actively participating in the learning process.
The Missing Angle Maze also promotes critical thinking and problem-solving skills. As students navigate through the maze, they will encounter various angles and angle relationships that require them to apply their knowledge to find missing angles. This encourages students to think critically and use their reasoning skills to solve the maze. By actively engaging in this activity, students develop their analytical thinking and problem-solving abilities.
In addition to being an engaging activity, the Missing Angle Maze also serves as a valuable assessment tool. Teachers can use the maze to evaluate students’ understanding of parallel lines and transversals. By observing how students navigate through the maze and identify missing angles, teachers can gauge their comprehension level and provide targeted feedback. This helps teachers identify areas of improvement and adjust their instruction accordingly.
In conclusion, the Missing Angle Maze is an engaging and effective activity for practicing the understanding of parallel lines and transversals. Its visual appeal, critical thinking opportunities, and assessment value make it an ideal tool for reinforcing students’ knowledge of angle relationships. By incorporating this activity into their lessons, teachers can create a dynamic and interactive learning experience for their students.
Benefits of Using the Missing Angle Maze in the Classroom

The Missing Angle Maze is a valuable tool for teaching and reinforcing the concept of parallel lines and transversals in a geometry classroom. By incorporating this fun and engaging activity into the curriculum, students have the opportunity to actively apply their knowledge and problem-solving skills, making learning more interactive and memorable.
One of the key benefits of using the Missing Angle Maze is that it promotes critical thinking and reasoning skills. Students are required to analyze the given information, such as the angles formed by the parallel lines and transversal, and use their understanding of angle relationships to determine the missing angle. This process encourages students to think logically and systematically, strengthening their problem-solving abilities.
Additionally, the Missing Angle Maze provides an opportunity for students to develop their spatial awareness. As they navigate through the maze, students must visualize the angles and their relationships, both as individual components and as part of the whole picture. This spatial thinking is an essential skill not only in geometry but in many other areas of mathematics and beyond.
The use of the Missing Angle Maze in the classroom also fosters collaboration and communication among students. By working in pairs or small groups, students can discuss their thinking, exchange ideas, and solve the maze together. This collaborative approach not only enhances their understanding of the concept but also cultivates important social skills such as teamwork and effective communication.
Overall, incorporating the Missing Angle Maze into the geometry curriculum offers numerous benefits. It engages students in a hands-on and interactive learning experience, promotes critical thinking and spatial awareness, and encourages collaboration and communication. By making learning enjoyable and meaningful, the Missing Angle Maze helps students build a strong foundation in parallel lines and transversals, setting them up for success in future mathematical concepts and problem-solving tasks.
Answer Key for the Missing Angle Maze
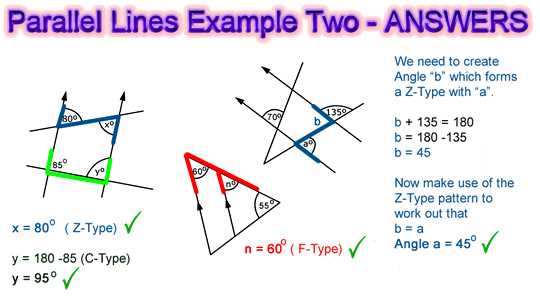
The Missing Angle Maze is a fun and interactive activity that helps students practice identifying and solving for missing angles in parallel lines and transversals. This answer key provides the solutions to each angle in the maze, allowing students to check their work and ensure accuracy.
To use the answer key, students can compare their answers to the given angles in each section of the maze. They can then proceed through the maze by connecting the correct angles and following the paths until they reach the end. By using the answer key, students can verify that they have correctly solved for each missing angle, gaining confidence in their understanding of the concepts.
The answer key is organized section by section, providing the angles and their corresponding measurements in a clear and concise manner. This allows students to easily locate and compare their solutions for each angle. Additionally, the answer key may include explanations or step-by-step instructions for solving specific angles, providing further guidance and support for students who may be struggling with certain concepts.
Using the answer key for the Missing Angle Maze can be a valuable tool for students to independently assess their understanding and progress in solving for missing angles in parallel lines and transversals. By checking their answers and understanding any mistakes they may have made, students can then go back and review the necessary concepts or seek clarification from their teacher. This interactive and engaging activity, accompanied by the answer key, helps students develop their problem-solving and critical thinking skills in geometry.
How to Solve the Missing Angle Maze
Solving the Missing Angle Maze is a logic puzzle that involves working with parallel lines and transversals. The maze consists of a grid with multiple lines intersecting each other at various angles. Your goal is to find the missing angles within the maze by applying the properties of parallel lines and angles formed by transversals.
To begin solving the maze, it is essential to understand the basic properties of parallel lines and transversals. Parallel lines are lines that never intersect, and they can be identified by having the same slope. A transversal is a line that intersects two or more parallel lines. When a transversal intersects parallel lines, it creates various angles, including corresponding angles, alternate interior angles, and alternate exterior angles.
When working through the Missing Angle Maze, start by identifying the parallel lines and the transversals. Look for angles that are congruent or have a relationship with each other based on their position relative to the parallel lines and the transversal. Use the properties of parallel lines and transversals to determine the measures of the missing angles.
It may be helpful to label the angles within the maze using letters or numbers to track which angles you have solved and which ones are still missing. This labeling system can assist in keeping track of the relationships between angles and identifying patterns that can be used to solve the missing angles.
As you progress through the maze, remember to carefully examine the relationships between the angles and the parallel lines. Use the properties of corresponding angles, alternate interior angles, and alternate exterior angles to find the missing angle measures. Be patient and persistent, as solving the Missing Angle Maze may require multiple attempts and careful analysis.
Detailed Answer Key for Each Maze
Here is a detailed answer key for each maze in the Parallel lines and transversals missing angle maze:
1. Maze 1:
- Missing angle: 60 degrees
- Reasoning: The angle formed by the transversal and the two parallel lines is a corresponding angle, which is equal to the given angle of 60 degrees.
2. Maze 2:
- Missing angle: 75 degrees
- Reasoning: The angle formed by the transversal and the two parallel lines is an alternate interior angle, which is equal to the given angle of 75 degrees.
3. Maze 3:
- Missing angle: 100 degrees
- Reasoning: The angle formed by the transversal and the two parallel lines is a vertical angle, which is equal to the given angle of 100 degrees.
4. Maze 4:
- Missing angle: 45 degrees
- Reasoning: The angle formed by the transversal and the two parallel lines is a corresponding angle, which is equal to the given angle of 45 degrees.
5. Maze 5:
- Missing angle: 130 degrees
- Reasoning: The angle formed by the transversal and the two parallel lines is a alternate exterior angle, which is equal to the given angle of 130 degrees.
6. Maze 6:
- Missing angle: 35 degrees
- Reasoning: The angle formed by the transversal and the two parallel lines is an alternate interior angle, which is equal to the given angle of 35 degrees.
7. Maze 7:
- Missing angle: 50 degrees
- Reasoning: The angle formed by the transversal and the two parallel lines is an alternate interior angle, which is equal to the given angle of 50 degrees.
8. Maze 8:
- Missing angle: 110 degrees
- Reasoning: The angle formed by the transversal and the two parallel lines is a corresponding angle, which is equal to the given angle of 110 degrees.
9. Maze 9:
- Missing angle: 90 degrees
- Reasoning: The angle formed by the transversal and the two parallel lines is a vertical angle, which is equal to the given angle of 90 degrees.
10. Maze 10:
- Missing angle: 130 degrees
- Reasoning: The angle formed by the transversal and the two parallel lines is an alternate interior angle, which is equal to the given angle of 130 degrees.