
If you’re looking to improve your understanding of parent functions and how they can be transformed, then you’ve come to the right place. This worksheet is designed to provide you with a comprehensive overview of parent functions and their transformations, along with detailed answers to help you gauge your progress.
The worksheet covers a range of essential concepts, including the definition and characteristics of parent functions such as linear, quadratic, exponential, and logarithmic functions. By studying these key functions, you’ll gain a solid foundation to build upon when it comes to understanding transformations.
Speaking of transformations, the worksheet delves into the various ways in which parent functions can be altered. From shifts, stretches, and compressions to reflections and combinations of transformations, you’ll have the opportunity to explore and practice each type of transformation with a variety of example problems.
With the provided answers, you can check your work and correct any mistakes, ensuring that you grasp the concepts fully. This interactive and comprehensive worksheet will not only help you ace your math exams, but it will also give you a deeper understanding of the fascinating world of parent functions and their transformations.
Understanding parent functions
When studying functions and their transformations, it is important to first have a solid understanding of parent functions. Parent functions are basic functions that serve as a foundation for more complex functions. They can be thought of as the “original” or “default” functions from which other functions are derived.
One example of a commonly used parent function is the linear function, which has the form y = mx + b, where m is the slope and b is the y-intercept. The linear function represents a straight line on a graph and is often used to model relationships between two variables.
Another example of a parent function is the quadratic function, which has the form y = ax^2 + bx + c. The quadratic function represents a parabola on a graph and is often used to model situations that involve curvature.
Understanding the characteristics and behavior of these parent functions is essential when studying their transformations. Transformations involve altering the parent function by modifying its shape, position, or both. Common transformations include translations (shifting the graph horizontally or vertically), reflections (flipping the graph over an axis), and stretches/compressions (altering the graph’s width or height).
Summary:
- Parent functions are basic functions that serve as a foundation for more complex functions.
- Examples of parent functions include linear functions and quadratic functions.
- Understanding the characteristics and behavior of parent functions is important when studying transformations.
- Transformations involve altering the parent functions by modifying their shape, position, or both.
- Common transformations include translations, reflections, and stretches/compressions.
Types of Parent Functions
The concept of parent functions is an essential part of understanding how functions behave and how they can be transformed. A parent function is the simplest or most basic function in a family of functions. It serves as a reference point or starting point from which other functions in the family are derived.
There are several common types of parent functions that are frequently encountered in algebra and calculus. These include:
- Linear function (y = mx + b): This is the simplest type of parent function, represented by a straight line with a constant slope (m) and a y-intercept (b).
- Quadratic function (y = ax^2 + bx + c): This function represents a parabola and is characterized by a squared term (x^2), a linear term (bx), and a constant term (c).
- Exponential function (y = a^x): This function has a constant base (a) raised to the power of x. It exhibits exponential growth or decay.
- Absolute value function (y = |x|): This function represents the distance of a point from the origin on a number line. It is characterized by a V-shaped graph with a vertex at (0, 0).
- Square root function (y = √x): This function represents the principal square root of x. It has a curved graph and is defined only for non-negative values of x.
These are just a few examples of the most common parent functions. Each function type has its own unique properties, graph, and behavior. By understanding the characteristics of these parent functions, it becomes easier to understand and analyze more complex functions that are derived from them through transformations.
The properties of parent functions are important to understand in order to grasp the concept of transformations. Parent functions are the simplest form of a function and serve as the building blocks for other functions. They provide a baseline for comparison when transforming functions.
Linear Functions:
A linear function has the form f(x) = mx + b, where m represents the slope and b represents the y-intercept. The slope determines the steepness of the line, while the y-intercept is the point where the line crosses the y-axis. The parent function for linear functions is f(x) = x, where the slope is 1 and the y-intercept is 0.
Quadratic Functions:
A quadratic function has the form f(x) = ax^2 + bx + c, where a, b, and c are constants. The graph of a quadratic function is a parabola. The parent function for quadratic functions is f(x) = x^2, where a = 1, b = 0, and c = 0. The vertex of the parabola is at the origin (0, 0) and the shape of the graph is determined by the value of a.
Absolute Value Functions:
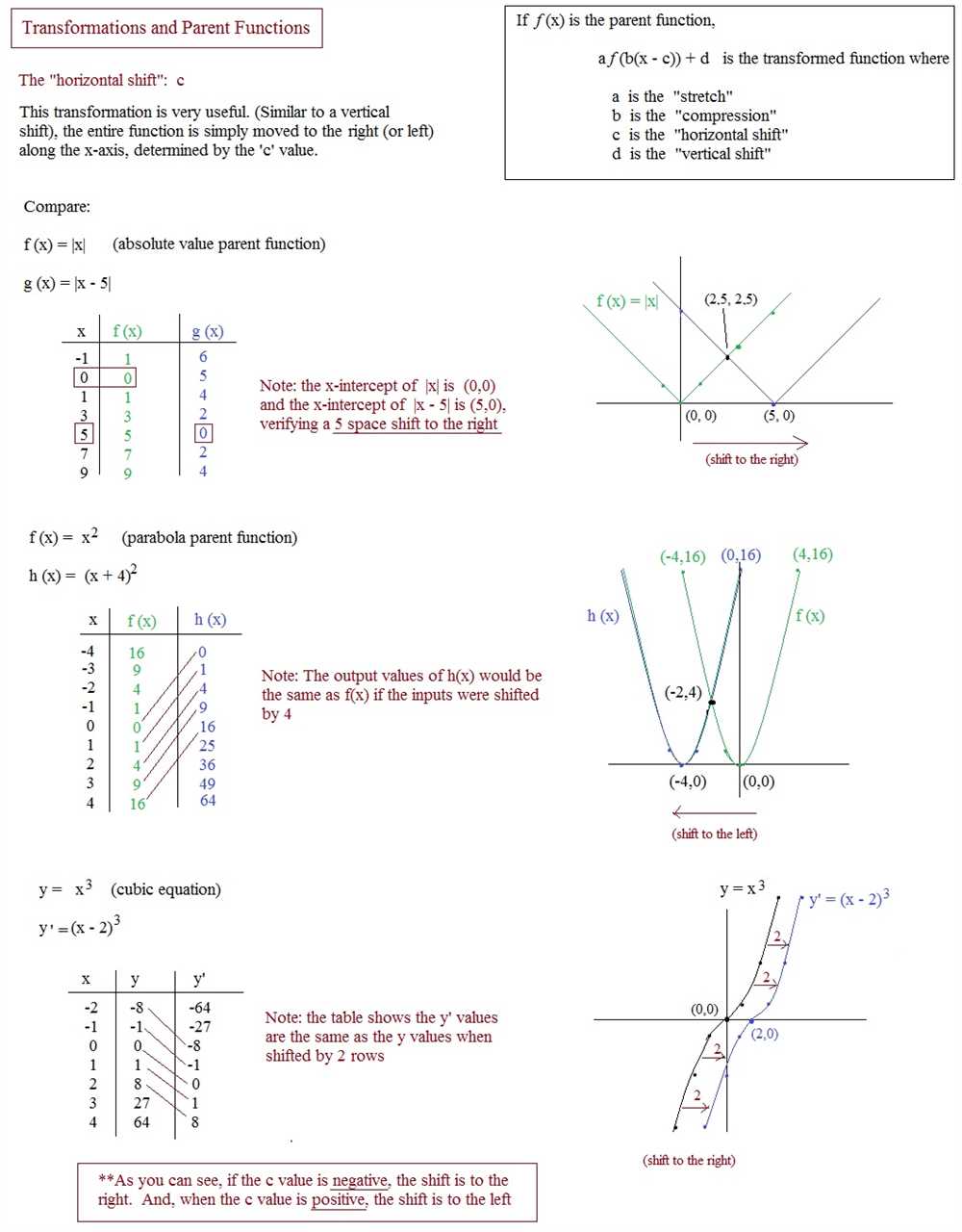
An absolute value function has the form f(x) = |x|. The graph of an absolute value function is a V-shaped graph. The parent function for absolute value functions is f(x) = |x|, where the graph passes through the origin (0, 0). The absolute value function reflects any negative values of x to positive values, which causes the graph to take the shape of a V.
Square Root Functions:

A square root function has the form f(x) = √x. The graph of a square root function is a curve that starts at the origin and continues to rise to the right. The parent function for square root functions is f(x) = √x, where the graph starts at the origin (0, 0). The domain of a square root function is limited to non-negative values of x.
Exponential Functions:
An exponential function has the form f(x) = a^x, where a is a constant and x represents an exponent. The graph of an exponential function is a curve that either rises or falls exponentially. The parent function for exponential functions is f(x) = b^x, where a = b and x = 1. The graph passes through the point (0, 1).
Graphing parent functions
When studying functions, it is important to understand the concept of parent functions. A parent function is the most basic form of a function, without any transformations or modifications. It serves as a reference point for understanding how different transformations affect the graph of a function.
There are several common parent functions that are frequently studied in mathematics, including the linear function, quadratic function, absolute value function, square root function, and cubic function. Each of these functions has a unique graph and can be easily identified by their equation.
To graph a parent function, it is helpful to understand its key characteristics. For example, the linear function has a constant slope, the quadratic function has a parabolic shape, and the absolute value function has a “v” shape. These characteristics can help you visualize the graph and make predictions about its behavior.
Once you understand the basic shape of a parent function, you can then apply transformations to create new graphs. These transformations include translations, reflections, stretches, and compressions. Each transformation affects the graph in a specific way, such as shifting it horizontally or vertically, flipping it across an axis, or changing its size.
By experimenting with different transformations, you can gain a deeper understanding of how each one affects the graph of a parent function. This knowledge is important for solving mathematical problems, analyzing real-world data, and making predictions based on mathematical models.
Exploring transformations
Transformations play a crucial role in understanding how functions can be manipulated and altered. By applying various transformations to a parent function, we can observe how its graph changes and gain insights into the behavior of different mathematical functions.
A common transformation is a translation, which moves a function horizontally or vertically. A positive translation in the x-direction shifts the graph to the left, while a negative translation shifts it to the right. Similarly, a positive translation in the y-direction moves the graph up, while a negative translation moves it down. These translations can help us analyze how changes in the input or output values affect the overall shape and position of the function.
Another transformation, scaling, alters the size of the function. Multiplying the input value by a constant stretches or compresses the graph horizontally, while multiplying the output value stretches or compresses it vertically. Changing the scale factor impacts how quickly the function increases or decreases and can reveal patterns and relationships between different parts of the graph.
Reflections and rotations are also transformations that can be applied to functions. Reflections flip the function across an axis, while rotations rotate it around a fixed point. These transformations provide a different perspective on the function and highlight symmetries and asymmetries within the graph.
By exploring and experimenting with these transformations, mathematicians can gain a deeper understanding of the behavior of functions and how their properties can change. These insights are crucial in various fields, such as physics, engineering, and computer science, where understanding and manipulating functions is essential for solving real-world problems.
Types of Transformations

In mathematics, transformations are used to modify the shape or position of a given function. There are several types of transformations that can be applied to parent functions, such as translation, reflection, vertical stretch/compression, and horizontal stretch/compression.
Translation: A translation of a function shifts the entire graph horizontally or vertically. The translated function has the same shape as the parent function, but its position is modified. A horizontal translation moves the graph left or right, while a vertical translation moves the graph up or down.
Reflection: A reflection of a function reflects the graph over a given line (usually the x-axis or y-axis). This results in a mirror image of the original graph. A reflection over the x-axis changes the sign of the y-coordinates, while a reflection over the y-axis changes the sign of the x-coordinates.
Vertical Stretch/Compression: A vertical stretch or compression modifies the vertical scale of a function. A vertical stretch increases the distance between points on the graph, making it appear taller and narrower. A vertical compression decreases the distance between points, making the graph shorter and wider. These transformations are achieved by multiplying the function by a constant value greater than 1 (stretch) or between 0 and 1 (compression).
Horizontal Stretch/Compression: A horizontal stretch or compression modifies the horizontal scale of a function. A horizontal stretch increases the distance between points on the graph, making it appear wider. A horizontal compression decreases the distance between points, making the graph narrower. These transformations are achieved by dividing the x-values of the function by a constant value greater than 1 (stretch) or between 0 and 1 (compression).
By understanding and applying these types of transformations, mathematicians can manipulate parent functions to create a variety of graphs and study how they behave.
Applying transformations to parent functions
When studying parent functions, it is important to understand how they can be transformed using various transformations. By applying transformations, we can shift, stretch, compress, and reflect the graphs of parent functions to create new functions.
One common transformation is shifting the graph horizontally or vertically. This can be done by adding or subtracting values inside the function. For example, if we have the equation y = f(x), shifting the graph horizontally by adding a value would result in y = f(x + h), where h represents the amount of horizontal shift. Similarly, shifting the graph vertically can be achieved by adding or subtracting a value outside the function, resulting in y = f(x) + k, where k represents the amount of vertical shift.
Examples:

- Shifting the graph of y = x^2 horizontally to the left by 3 units: y = (x + 3)^2.
- Shifting the graph of y = x^2 vertically upwards by 2 units: y = x^2 + 2.
Another common transformation is stretching or compressing the graph. This can be done by multiplying or dividing the function by a value. A multiplication greater than 1 stretches the graph vertically, while a multiplication between 0 and 1 compresses the graph vertically. Similarly, a multiplication greater than 1 compresses the graph horizontally, while a multiplication between 0 and 1 stretches the graph horizontally.
Examples:
- Stretching the graph of y = x^2 vertically by a factor of 2: y = 2x^2.
- Compressing the graph of y = x^2 horizontally by a factor of 0.5: y = (0.5x)^2.
Lastly, reflection is another transformation that can be applied to parent functions. Reflecting a graph over the x-axis is done by multiplying the function by -1, while reflecting it over the y-axis is achieved by multiplying the x-values by -1.
Examples:
- Reflecting the graph of y = x^2 over the x-axis: y = -x^2.
- Reflecting the graph of y = x^2 over the y-axis: y = (-x)^2.
By understanding and applying these transformations, we can create a wide variety of functions that have different shapes and characteristics compared to their parent functions. This provides us with a powerful toolkit for analyzing and understanding the behavior of functions in mathematics and other fields.