
Understanding the parts of a circle is a fundamental concept in mathematics. A circle is a two-dimensional geometric shape that consists of all points in a plane that are equidistant from a fixed point called the center. In order to fully comprehend the properties and characteristics of circles, it is important to be able to identify and define its various parts.
One of the key components of a circle is the radius. The radius is the distance from the center of the circle to any point on its circumference. It is represented by the lowercase letter “r” in mathematical equations. The radius can also be used to calculate other important measurements of a circle, such as its circumference and area.
Another significant part of a circle is the diameter. The diameter is defined as a straight line that passes through the center of the circle and connects two points on its circumference. It is represented by the uppercase letter “D” or “d” in mathematical equations. The diameter is the longest chord of a circle and is equal to twice the radius.
In addition to the radius and diameter, circles also have an important measurement known as the circumference. The circumference of a circle is the distance around its outer edge. It is equal to the product of the diameter and the mathematical constant pi (π), which is approximately 3.14159. The circumference can be calculated using the formula C = πd or C = 2πr, where C represents the circumference, d represents the diameter, and r represents the radius.
By understanding and being able to identify the different parts of a circle, students can better comprehend the relationships and properties of circles. A parts of a circle worksheet is a valuable educational tool that provides practice in identifying and solving problems related to circles. This worksheet typically includes questions that require students to calculate the radius, diameter, or circumference of a circle given certain information. The answers to these worksheets are often provided in a PDF format, allowing students to check their work and reinforce their understanding of the topic.
Understanding the Parts of a Circle
When studying geometry, it is crucial to have a solid understanding of the various parts of a circle. Circles are a fundamental shape that can be found in many real-world applications, so knowing their components and properties is essential.
One of the key elements of a circle is the center. The center of a circle is the point that is equidistant from all the points on the circumference. It acts as the focal point of the circle and is often denoted by the letter “O”. The center is crucial in determining many other properties of the circle, such as the radius and diameter.
The radius is another vital component of a circle. The radius is the distance from the center of the circle to any point on the circumference. It is often denoted by the letter “r”. The radius plays a significant role in calculating other measurements, such as the circumference and area of the circle. The radius of a circle is always half of the diameter.
The diameter is the longest chord (a line that connects any two points on the circumference) that passes through the center of the circle. It is a crucial measurement, as it determines the size of the circle. The diameter is twice the length of the radius. It is often denoted by the letter “d”.
Other important parts of a circle include the circumference, which is the perimeter of the circle, and the arc, which is a portion of the circumference. The sector is a region enclosed by two radii and the arc between them. These components all work together to create the geometry and properties of a circle. By understanding each part, individuals can solve various circle-related problems and apply their knowledge to real-world situations.
The Definition of a Circle
A circle is a closed shape that is perfectly round. It is one of the most fundamental geometric shapes, and its properties and characteristics are well-studied in mathematics. A circle is defined as the set of all points in a plane that are equidistant from a fixed center point. This fixed center point is also called the center of the circle. The distance from the center of the circle to any point on its boundary is called the radius of the circle.
A circle is often represented using the symbol “O” or by drawing a closed curve with curved lines. It is important to note that a circle has no straight sides or corners. Instead, it has a curved boundary that forms a continuous loop. This boundary is also referred to as the circumference of the circle.
A circle can be further divided into different parts and components, each with its own unique definition. Some common parts include the diameter, chord, sector, and segment. The diameter of a circle is a straight line that passes through the center and divides the circle into two equal halves. A chord is a straight line segment that connects two points on the circumference of the circle. A sector is a region between two radii and the corresponding arc, while a segment is a region between a chord and the corresponding arc.
Understanding the different parts of a circle and their relationships is important in various fields such as geometry, physics, and engineering. Circles have numerous applications in real-world situations, such as calculating the area and circumference, designing circular structures, and analyzing circular motion. Whether it is in the form of a wheel, the orbit of a planet, or the shape of a coin, circles play a significant role in our everyday lives.
The Center of a Circle
The center of a circle is a fundamental concept in geometry. It is the point that is equidistant from all points on the circle’s circumference. In other words, if you were to draw a straight line from the center of the circle to any point on its edge, the length of that line would be the same for all points.
The center of a circle plays a crucial role in determining many properties of the circle. For example, the radius of the circle is the distance from the center to any point on its edge. This distance remains constant for all points on the circle.
The center of a circle is denoted by the letter “O” in geometric representations. It is often used as a reference point for other measurements and calculations involving the circle. By knowing the center of a circle, you can easily determine its radius, diameter, and circumference.
The concept of the center of a circle is important in various fields, including mathematics, engineering, and architecture. It helps in designing and constructing circular structures, such as wheels, gears, and round buildings. Understanding the properties and relationships involving the center of a circle is essential for solving geometric problems and analyzing circular objects in real-world applications.
The Radius of a Circle

In geometry, a circle is a two-dimensional shape that is perfectly round and consists of all points at a fixed distance from its center. One of the key features of a circle is its radius, which is the distance from the center of the circle to any point on its circumference.
The radius of a circle is always half of its diameter. It can be denoted by the letter “r” and is typically measured in units such as centimeters or inches. The radius is an important measurement when calculating various properties of a circle, including its circumference, area, and arc length.
To calculate the circumference of a circle, you can use the formula C = 2πr, where “C” represents the circumference and “π” is a mathematical constant approximately equal to 3.14159. By knowing the radius, you can easily determine the size of the circle’s circumference.
The area of a circle can be calculated using the formula A = πr^2, where “A” represents the area. This formula indicates that the area of a circle is directly proportional to the square of its radius. Therefore, increasing the radius will significantly increase the area of the circle.
The radius also plays an important role in determining the length of an arc on a circle. An arc is a portion of the circumference of the circle, and its length can be calculated using the formula L = 2πrθ/360, where “L” represents the arc length and “θ” is the central angle of the arc in degrees.
In conclusion, the radius of a circle is a crucial measurement that helps determine its circumference, area, and arc length. Understanding the concept of the radius is essential when working with circles in geometry and other mathematical disciplines.
The Diameter of a Circle
The diameter of a circle is one of its most important properties. It is a line segment that passes through the center of the circle and connects two points on its circumference. The diameter is the longest possible distance that can be measured within a circle. It is twice the length of the radius, which is the distance from the center to any point on the circumference.
The formula to calculate the diameter of a circle is: diameter = 2 * radius. This means that if you know the radius of a circle, you can easily find its diameter by multiplying the radius by 2. Similarly, if you know the diameter, you can find the radius by dividing the diameter by 2.
Understanding the diameter of a circle is crucial when dealing with various geometric calculations. For example, the diameter is used to find the circumference of a circle using the formula: circumference = π * diameter (where π is a mathematical constant approximately equal to 3.14159).
Another important property of the diameter is that it divides the circle into two equal halves called semicircles. Each semicircle has a radius equal to half of the diameter. This property is useful when calculating the areas of circles, as the area of a circle can be found using the formula: area = π * radius^2. By knowing the diameter, you can easily find the radius and therefore calculate the area.
In conclusion, the diameter of a circle plays a crucial role in various geometric calculations and relationships. It is the longest possible distance within a circle, and it can be used to find the circumference, radius, and area of a circle. Understanding the diameter helps to unlock the many properties of circles and their applications in mathematics and real-life scenarios.
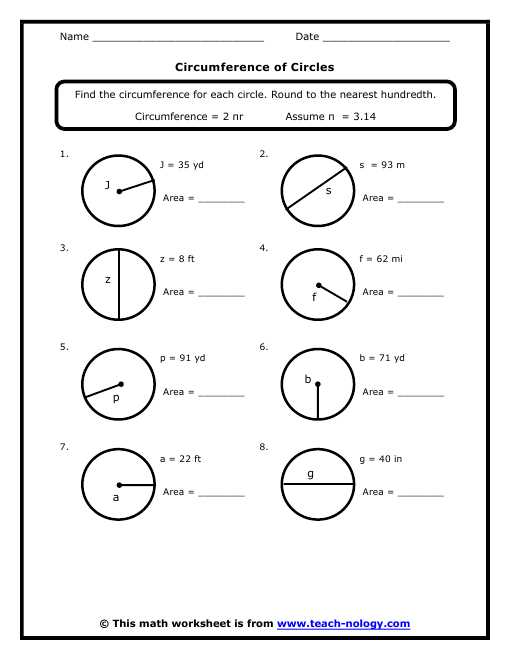
Calculating the Circumference of a Circle
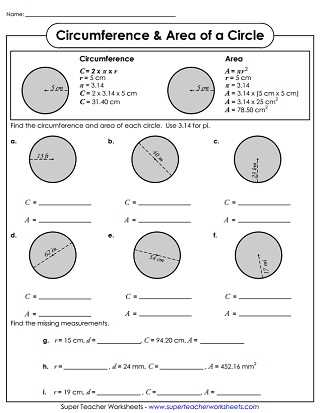
When studying circles, one of the key measurements we often need to calculate is the circumference. The circumference of a circle is the distance around its outer edge and can be thought of as the perimeter of the circle. It’s an essential concept in geometry and has real-world applications in fields like engineering and architecture.
To calculate the circumference of a circle, we need to know its radius or diameter. The radius is the distance from the center of the circle to any point on its edge, while the diameter is twice the radius. The formula to calculate the circumference is C = π * d (where d represents the diameter) or C = 2 * π * r (where r represents the radius). Here, π (pi) is a mathematical constant approximately equal to 3.14159, which is often rounded to 3.14 for practical purposes.
To illustrate the calculation of the circumference, let’s consider an example. Suppose we have a circle with a diameter of 10 centimeters. We can use the formula C = π * d to find the circumference. Substituting the given values, we get C = 3.14 * 10 = 31.4 centimeters. Therefore, the circumference of this circle is 31.4 centimeters.
It’s important to note that the units of measurement must be consistent when calculating the circumference. If the diameter is given in inches, the circumference will be in inches as well. Similarly, if the diameter is given in meters, the circumference will be in meters. Paying attention to units ensures accurate calculations and meaningful results.
The Circumference Formula
The circumference of a circle is the distance around the outside edge of the circle. It is an important measurement to know when working with circles and is often used in various mathematical calculations and real-world applications. The formula for finding the circumference of a circle is:
Circumference = 2πr
In this formula, “r” represents the radius of the circle, which is the distance from the center of the circle to any point on its edge. “π” (pi) is a mathematical constant that represents the ratio of the circumference of any circle to its diameter, approximately equal to 3.14159.
To use the circumference formula, simply plug in the value of the radius into the equation and perform the necessary calculations. Once you have the circumference, you can use it to find other important measurements, such as the diameter or the area of the circle.
Knowing the circumference of a circle can be useful in a variety of situations. For example, if you are planning to build a fence around a circular garden, understanding the circumference will help you determine how much fencing material you will need. Similarly, if you are trying to calculate the distance traveled by a wheel on a vehicle, knowing the circumference of the wheel will help you determine the distance covered with each revolution.
In summary, the circumference formula of a circle is an essential tool in mathematics and real-world applications. It allows you to calculate the distance around the outside edge of a circle and is used in various calculations related to circles. Understanding this formula can help you solve problems and make accurate measurements involving circles.
Examples of Calculating Circumference
The circumference of a circle can be calculated using the formula C = 2πr, where C represents the circumference and r represents the radius of the circle. By knowing the radius of a circle, we can easily determine its circumference.
Example 1:
Let’s say we have a circle with a radius of 5 units. Using the formula C = 2πr, we can substitute the value of the radius to find the circumference.
C = 2π(5) = 10π units.
So, the circumference of this circle is 10π units.
Example 2:
Consider a circle with a radius of 8 centimeters. To find the circumference, we use the formula C = 2πr.
C = 2π(8) = 16π centimeters.
Therefore, the circumference of this circle is 16π centimeters.
Example 3:
Suppose we have a circle with a radius of 3.5 meters. We can find the circumference by substituting the radius into the formula C = 2πr.
C = 2π(3.5) = 7π meters.
Hence, the circumference of this circle is 7π meters.
In summary, the circumference of a circle can be calculated by multiplying the radius by 2π. Having the value of the radius, we can easily find the circumference of any circle using this formula. It allows us to determine the distance around the circle and is an important measurement in various mathematical and real-world applications.