
Precalculus is a fundamental course that lays the groundwork for advanced mathematical concepts. As the name suggests, it serves as a precursor to calculus, equipping students with necessary skills and knowledge before tackling more complex mathematical topics. To assess students’ understanding of the subject, precalculus final exams are conducted at the end of the course.
This article aims to provide a comprehensive guide to a precalculus final exam, including a breakdown of the topics covered, key concepts to focus on, and example questions with their solutions. Whether you’re a student preparing for your upcoming exam or a teacher looking for resources to help your students succeed, this guide is here to assist you along the way.
The precalculus final exam typically covers a range of topics, including functions, algebraic equations, trigonometry, exponential and logarithmic functions, and analytic geometry. Each section requires a solid understanding of the underlying principles and techniques. Working through practice problems is crucial to reinforce your knowledge and strengthen your problem-solving skills in these areas.
Overview of the PreCalculus Final Exam

The PreCalculus final exam is an important assessment that tests students’ understanding of the concepts and skills covered throughout the course. It is designed to evaluate their proficiency in topics such as functions, trigonometry, algebra, and analytic geometry. The exam typically consists of a variety of question types, including multiple-choice, short-answer, and problem-solving questions.
One of the key areas covered in the precalculus final exam is functions. Students are expected to demonstrate their ability to analyze and graph various types of functions, including linear, quadratic, exponential, logarithmic, and trigonometric functions. They should understand the properties of these functions and be able to apply them in real-life situations.
Trigonometry is another important component of the precalculus final exam. Students should have a solid understanding of trigonometric functions, identities, and equations. They should be able to solve trigonometric equations, find missing side lengths and angles in right triangles, and apply trigonometric functions to solve real-world problems.
Algebraic skills are also assessed in the precalculus final exam. Students should be proficient in manipulating algebraic expressions, solving equations and inequalities, and simplifying rational expressions. They should also have a good understanding of sequences and series, as well as matrices and determinants.
Finally, the precalculus final exam covers topics in analytic geometry, such as conic sections and polar coordinates. Students should be able to identify and graph various conic sections, including circles, ellipses, parabolas, and hyperbolas. They should also be familiar with converting between rectangular and polar coordinates and be able to graph equations in polar coordinates.
In conclusion, the precalculus final exam is a comprehensive assessment that tests students’ knowledge and skills in functions, trigonometry, algebra, and analytic geometry. It requires a solid understanding of the concepts and the ability to apply them to solve problems. By thoroughly reviewing and practicing these topics, students can prepare themselves for success on the final exam.
Format and Structure of the Precalculus Final Exam
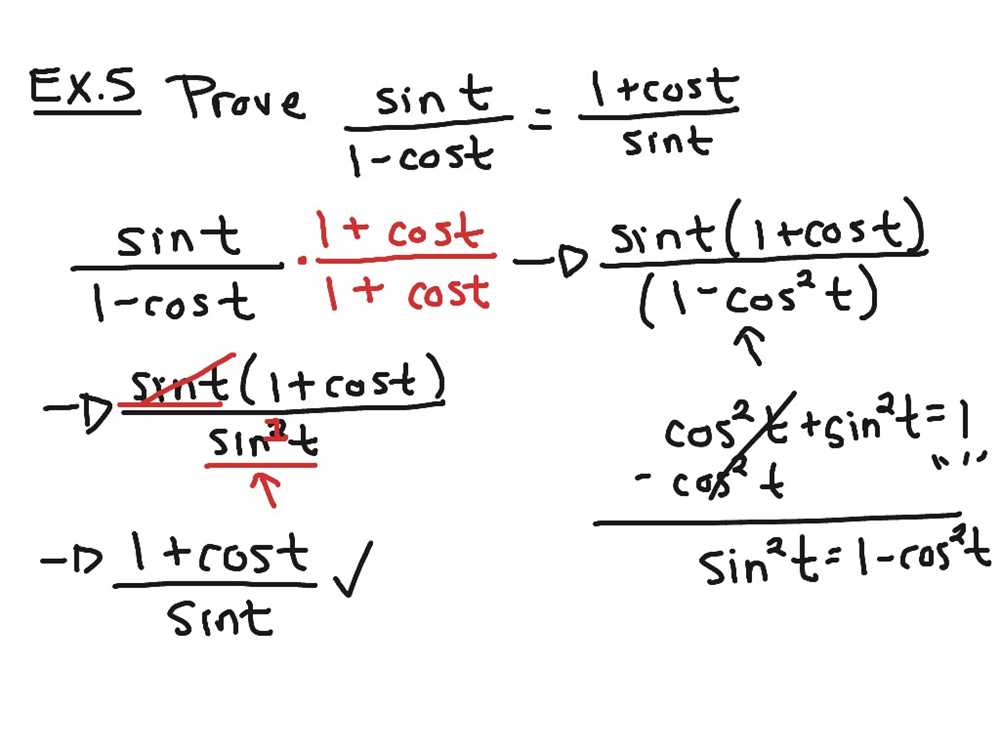
The precalculus final exam is a comprehensive assessment that evaluates students’ understanding and knowledge of the topics covered throughout the course. It is typically designed to test students’ ability to apply mathematical concepts, solve problems, and analyze mathematical situations.
Usually, the precalculus final exam consists of a mixture of multiple-choice questions, short answer questions, and longer, more involved problems that require students to show their problem-solving skills. This varied format allows instructors to assess students’ understanding from different angles and levels of complexity.
The exam is often divided into sections or topics, such as algebraic functions, trigonometry, logarithmic and exponential functions, and analytic geometry. Each section may have a different weight in terms of the overall grade. For example, the algebraic functions section may contribute 30% of the total grade, while trigonometry may contribute 20%. This structure ensures that students are tested on all important topics covered in the course.
Additionally, instructors may include a section that requires students to demonstrate their understanding of mathematical concepts through written explanations or proofs. This section allows students to showcase their ability to articulate mathematical ideas clearly and concisely.
Overall, the format and structure of the precalculus final exam aim to comprehensively assess students’ knowledge and skills acquired throughout the course. By including a mix of question types and covering all relevant topics, the exam provides a fair and accurate representation of students’ abilities in precalculus.
Tips for preparing for the precalculus final exam

Preparing for the precalculus final exam can be a challenging task, but with the right strategies and techniques, you can improve your chances of success. Here are some tips to help you get ready:
- Review all the concepts: Make sure you have a thorough understanding of all the topics covered in the course. This includes functions, trigonometry, algebraic equations, and more. Go through your notes and textbooks to reinforce your knowledge.
- Practice, practice, practice: One of the best ways to prepare for any math exam is by solving practice problems. Look for precalculus practice exams or worksheets and solve a variety of problems to familiarize yourself with different types of questions.
- Create a study plan: Break down your study sessions into manageable chunks and allocate specific time slots for each topic. This will help you stay organized and cover all the necessary material before the exam.
- Work with a study group: Collaborating with classmates can be beneficial as you can discuss difficult concepts, share notes, and quiz each other. Explaining concepts to others can also help solidify your own understanding.
- Seek help when needed: If you are struggling with certain topics, don’t hesitate to seek help from your teacher, classmates, or tutoring services. Understanding any areas of confusion will be crucial for success.
- Review past exams: If your teacher provides past exams or sample questions, make sure to review them. This will give you an idea of the format and types of questions you can expect on the final exam.
- Take care of yourself: Don’t forget to prioritize self-care during your exam preparation. Get enough sleep, eat well, and take breaks when needed. A well-rested and refreshed mind will be better equipped to tackle challenging math problems.
By following these tips, you can approach your precalculus final exam with confidence and increase your chances of achieving a high score. Good luck!
Important topics covered in the precalculus final exam
Precalculus is a foundational course that prepares students for advanced mathematical concepts. The final exam in precalculus assesses students’ understanding and mastery of various topics. Some of the important topics that are typically covered in the precalculus final exam include:
- Functions and their properties: This topic includes an examination of different types of functions, such as linear, quadratic, exponential, logarithmic, and trigonometric functions. Students are expected to understand the properties and characteristics of these functions, as well as their graphs and equations.
- Trigonometry: Trigonometry is a crucial part of precalculus. Students will be tested on their knowledge of trigonometric identities, solving trigonometric equations, and applying trigonometric functions to real-world problems.
- Sequences and series: This topic covers arithmetic and geometric sequences, as well as finite and infinite series. Students will be asked to find the nth term of a sequence, calculate the sum of a series, and determine the convergence or divergence of a series.
- Matrices and determinants: Students will be required to understand matrices and their operations, including addition, subtraction, multiplication, and finding the inverse of a matrix. They will also be expected to compute determinants of matrices.
- Conic sections: The final exam may include questions on conic sections, such as circles, ellipses, parabolas, and hyperbolas. Students need to be familiar with the equations, properties, and graphs of these conic sections.
The precalculus final exam serves as an important assessment tool to gauge students’ understanding of essential precalculus concepts and their ability to apply them. By covering these topics, the exam evaluates students’ readiness for more advanced mathematical courses and ensures that they have a solid foundation in precalculus before moving on to higher-level math.
Sample questions from the precalculus final exam

Here are some sample questions that may appear on a precalculus final exam. These questions cover a range of topics and difficulty levels, testing the students’ understanding of various precalculus concepts.
1. Find the domain and range of the function f(x) = 2x^2 – 3x + 1.
To find the domain of a function, we need to determine the set of all possible input values (x) for the function. In this case, there are no restrictions on the values x can take, so the domain is all real numbers (-∞, ∞). The range, on the other hand, can be determined by considering the graph of the function. Since the coefficient of x^2 is positive, the parabola opens upwards, indicating that the minimum value is at the vertex. The vertex can be calculated using the formula x = -b/2a, where a and b are the coefficients of x^2 and x, respectively. From there, we can find the corresponding y-value, which represents the minimum value. Therefore, the range of the function is [y-value, ∞).
2. Solve the equation log(base 2)x + log(base 2)(x – 3) = 2.
In order to solve this logarithmic equation, we can use the properties of logarithms. Adding two logarithms with the same base is the same as multiplying the expressions inside the logarithms. Therefore, we can rewrite the equation as log(base 2)(x(x-3)) = 2. Next, we can convert this logarithmic equation into exponential form: 2^2 = x(x-3). Simplifying further, we get 4 = x^2 – 3x. Rearranging the equation, we have x^2 – 3x – 4 = 0. Factoring or using the quadratic formula, we find that x = -1 and x = 4 are the solutions to the equation.
3. Determine the exact solutions of the trigonometric equation sin^2(2x) = cos(2x) in the interval [0, 2π].
To solve this trigonometric equation, we can use the trigonometric identities and properties. First, let’s rewrite the equation using the identity sin^2θ = 1 – cos^2θ: 1 – cos^2(2x) = cos(2x). Next, we can substitute u = cos(2x), resulting in the equation 1 – u^2 = u. Rearranging the equation, we have u^2 + u – 1 = 0. Solving this quadratic equation, we find that u = (sqrt(5) – 1)/2 and u = (-sqrt(5) – 1)/2. Since u = cos(2x), we can solve for x using the inverse cosine function: 2x = cos^(-1)((sqrt(5) – 1)/2) and 2x = cos^(-1)((-sqrt(5) – 1)/2). Finally, we divide both sides by 2 to obtain the exact solutions for x in the given interval.
These sample questions highlight the range of topics covered in a precalculus final exam, including functions, logarithms, and trigonometric equations. By mastering these concepts, students can demonstrate their understanding of precalculus and prepare for further studies in mathematics.
Strategies for solving different types of problems in the precalculus final exam
When preparing for a precalculus final exam, it’s important to have a clear understanding of the various types of problems that may be encountered. By familiarizing yourself with these problem types and employing effective strategies, you can increase your chances of success on the exam.
1. Algebraic problem solving: Many precalculus problems involve algebraic manipulations and equations. To solve these types of problems, start by carefully reading the problem and identifying all the variables and given information. Then, use algebraic techniques such as factoring, simplifying, or solving equations to find the solution.
Example strategy: Let’s say you come across a problem that involves solving a quadratic equation. Begin by identifying the quadratic equation and its coefficients. Then, use factoring or the quadratic formula to find the solutions of the equation. Verify your solutions by substituting them back into the original equation.
2. Trigonometric problem solving: Trigonometry is a key component of precalculus, and many problems in the final exam will require knowledge of trigonometric functions and identities. To solve these problems, start by identifying the given information and any trigonometric functions involved. Utilize the appropriate trigonometric identities and formulas to simplify the problem and find the solution.
Example strategy: Suppose you encounter a problem that involves finding the value of a trigonometric function at a given angle. Begin by identifying the functions involved and any related angles or values. Use the relevant trigonometric identity or formula to simplify the expression and evaluate the function at the given angle.
3. Word problems: Word problems in precalculus often require the application of mathematical concepts to real-life situations. To solve these types of problems, start by carefully reading the problem and identifying the relevant information and variables. Then, set up equations or inequalities that represent the given situation and use algebraic or trigonometric techniques to find the solution.
Example strategy: Imagine a word problem that involves finding the maximum area of a rectangular garden given a fixed amount of fencing. Begin by understanding the given information, such as the available fencing length and the relationship between the dimensions of the garden. Write an equation that relates the dimensions, and use techniques such as differentiation or completing the square to optimize the area and find the maximum value.
By employing effective strategies for each problem type, you can approach the precalculus final exam with confidence and increase your chances of earning a good grade.