If you are studying quadratic functions and need answers to a worksheet, you have come to the right place. This article will provide you with a comprehensive overview of the properties of quadratic functions and their corresponding worksheet answers. Quadratic functions are mathematical expressions that involve a variable raised to the power of two. They can be represented by equations in the form y = ax^2 + bx + c, where a, b, and c are constants.
One important property of quadratic functions is their graph shape. The graph of a quadratic function is a parabola, which can open upwards or downwards depending on the leading coefficient a. When a is positive, the parabola opens upwards, and when a is negative, the parabola opens downwards. This property is crucial in understanding the behavior of quadratic functions and their corresponding graphs.
Quadratic functions also possess a vertex, which is the point where the parabola reaches its maximum or minimum value. Finding the vertex of a quadratic function is essential in determining its key characteristics, such as the axis of symmetry and the maximum or minimum value of the function. This worksheet will provide practice problems on finding the vertex and understanding its significance in quadratic functions.
What are Quadratic Functions?
A quadratic function is a type of function that can be written in the form f(x) = ax^2 + bx + c, where a, b, and c are constants. The graph of a quadratic function is a parabola, which is a U-shaped curve.
The coefficient ‘a’ determines whether the parabola opens upwards (if a > 0) or downwards (if a < 0). The coefficient 'b' affects the position of the vertex and the direction of the parabola's axis of symmetry. The constant 'c' determines the y-intercept of the parabola.
Quadratic functions are versatile and widely used in various fields such as physics, engineering, economics, and computer science. They can describe a range of phenomena, such as projectile motion, population growth, and the behavior of financial markets.
When studying quadratic functions, it is important to understand their properties, such as the vertex, axis of symmetry, x-intercepts, and y-intercept. These properties can be determined using algebraic methods or by analyzing the graph of the function.
Why Study Quadratic Functions?
Quadratic functions play a crucial role in mathematics and various real-world applications. Understanding and studying quadratic functions provide valuable insights into numerous mathematical concepts and problem-solving techniques.
Modeling real-world situations: Quadratic functions can be used to model various real-world phenomena, such as the trajectory of a projectile, the shape of a water fountain, or the growth of a population. By studying quadratic functions, we gain the ability to understand and predict the behavior of these real-world situations.
Optimization: Quadratic functions are often involved in optimization problems, where we seek to maximize or minimize a particular quantity. For example, quadratic functions can help us find the maximum area enclosed by a given perimeter or the minimum cost of manufacturing a certain product. Being able to identify and solve optimization problems using quadratic functions is crucial in fields such as engineering, economics, and physics.
Graphical analysis: Quadratic functions have distinct graph shapes, known as parabolas. By studying the graph of a quadratic function, we can determine important properties, such as the vertex, axis of symmetry, maximum or minimum values, and x-intercepts. This graphical analysis is essential for understanding the behavior of quadratic functions and interpreting their meaning in real-world contexts.
Solving equations and inequalities: Quadratic functions are closely related to quadratic equations and inequalities. Studying quadratic functions helps us develop effective problem-solving strategies for solving these types of equations and inequalities. This skill is essential in various mathematical disciplines, such as algebra, calculus, and physics.
Overall mathematical understanding: Understanding quadratic functions provides a solid foundation for further mathematical exploration. Many advanced mathematical concepts, such as calculus and linear algebra, build upon the principles and techniques learned from studying quadratic functions. By delving into quadratic functions, we gain a deeper understanding of mathematical concepts and their interconnectedness.
In conclusion, studying quadratic functions is crucial to grasp fundamental mathematical concepts, solve real-world problems, and lay the groundwork for more advanced mathematical learning. The insights gained from studying quadratic functions have applications in various disciplines and contribute to a comprehensive understanding of mathematics.
Understanding the Properties of Quadratic Functions
A quadratic function is a function in the form of f(x) = ax^2 + bx + c, where a, b, and c are constants. Quadratic functions have several properties that can help us understand and analyze their behavior. By studying these properties, we can gain insights into how quadratic functions behave and make predictions about their graphs.
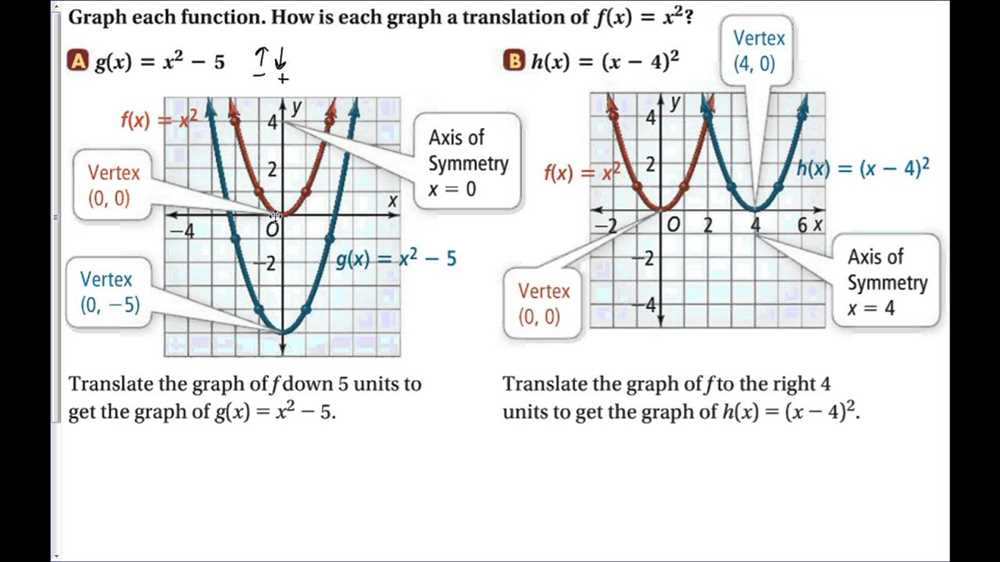
One important property of quadratic functions is the vertex. The vertex is the point on the graph where the function reaches its minimum or maximum value. It is represented by the coordinates (h, k), where h is the x-coordinate and k is the y-coordinate. The vertex can provide us with information about the direction the parabola opens and the axis of symmetry.
The axis of symmetry is a vertical line that passes through the vertex, dividing the parabola into two symmetrical halves. It is represented by the equation x = h, where h is the x-coordinate of the vertex. The axis of symmetry can help us determine the x-values where the function is symmetrical and where it reaches its minimum or maximum value.
Another property of quadratic functions is the discriminant. The discriminant is the expression b^2 – 4ac, which is found in the quadratic formula. It can help us determine the number and type of solutions that a quadratic equation has. If the discriminant is positive, the equation has two distinct real solutions. If the discriminant is zero, the equation has one real solution. And if the discriminant is negative, the equation has two complex solutions.
Understanding these properties of quadratic functions can enable us to solve equations, find the vertex and axis of symmetry, and analyze the behavior of the graph. Through practice and study, we can become proficient in manipulating and analyzing quadratic functions, allowing us to make accurate predictions and solve real-world problems.
Vertex Form of a Quadratic Function
A quadratic function is a type of polynomial function that can be written in the form f(x) = ax^2 + bx + c, where a, b, and c are constants. The graph of a quadratic function is a parabola, which can open upwards or downwards depending on the value of a.
The vertex form of a quadratic function is a different way to write the equation of a quadratic function. It is written as f(x) = a(x – h)^2 + k, where (h, k) represents the coordinates of the vertex of the parabola. The vertex form of a quadratic function allows us to easily identify the vertex and key characteristics of the parabola.
In the vertex form, the value of a determines the direction and width of the parabola. If a is positive, the parabola opens upwards and if a is negative, the parabola opens downwards. The value of h represents the x-coordinate of the vertex, while k represents the y-coordinate of the vertex.
By using the vertex form of a quadratic function, we can easily determine the vertex, axis of symmetry, and the y-intercept of the parabola. Additionally, we can determine whether the parabola opens upwards or downwards and whether it is wider or narrower compared to the standard form.
Overall, the vertex form of a quadratic function provides a concise and useful way to describe the characteristics of a parabola. It allows us to easily identify key points on the graph and make predictions about the behavior of the function. Understanding the vertex form can greatly enhance our understanding and analysis of quadratic functions.
Axis of Symmetry
In mathematics, a quadratic function is a polynomial function of the form f(x) = ax^2 + bx + c, where a, b, and c are constants and a is not equal to zero. Quadratic functions are known for their distinct graph shapes, featuring a parabolic curve.
One important concept in quadratic functions is the axis of symmetry. The axis of symmetry is a vertical line that divides the parabola into two symmetrical halves. It represents the line of symmetry for the graph of the quadratic function.
To find the axis of symmetry for a quadratic function, we need to use the formula x = -b/2a. The x-coordinate of the vertex of the parabola gives us the value for x in the axis of symmetry equation. The vertex is the highest or lowest point on the curve, depending on whether the parabola opens upward or downward.
The axis of symmetry is not only a vertical line that divides the graph, but it also has other important properties. For example, any point on the parabola that is equidistant from the axis of symmetry and the vertex will have the same y-coordinate, which can be determined using the quadratic function.
Understanding the concept of the axis of symmetry is essential in analyzing and graphing quadratic functions. It provides information about the symmetry and structure of the parabola, allowing us to quickly determine key features such as the vertex, maximum or minimum points, and the direction of the opening of the parabola.
Concavity of Quadratic Functions
In mathematics, quadratic functions are a type of polynomial function that can be written in the form f(x) = ax^2 + bx + c, where a, b, and c are constants. One important property of quadratic functions is their concavity, which describes the shape of the graph.
Concavity refers to the curvature of the graph of a quadratic function. It can either be concave up or concave down. A quadratic function is concave up if the coefficient ‘a’ is positive, and concave down if ‘a’ is negative. The value of ‘a’ determines the direction and steepness of the graph.
If a quadratic function is concave up, it means that the graph opens upward, forming a ‘U’ shape. The vertex of the parabola, where the graph reaches its minimum point, lies at the bottom of the ‘U’. On the other hand, if the quadratic function is concave down, the graph opens downward, forming an inverted ‘U’ shape. The vertex is located at the topmost point of the parabola, representing the maximum value.
To determine the concavity of a quadratic function, you can also examine the sign of the second derivative, denoted as f”(x). If f”(x) > 0, the function is concave up, and if f”(x) < 0, the function is concave down. The second derivative measures the rate at which the slope of the original function is changing.
Understanding the concavity of quadratic functions is crucial in analyzing graphs and solving quadratic equations. It helps us predict the behavior of the function and identify its maximum and minimum points. By studying the concavity, we gain insights into the overall shape and characteristics of quadratic functions.
Maximum and Minimum Points
In the study of quadratic functions, one of the key concepts is the identification of maximum and minimum points. These points represent the highest and the lowest values that the function can attain, respectively. By understanding how to find and interpret these points, we gain valuable information about the behavior and characteristics of the quadratic function.
To identify the maximum or minimum point of a quadratic function, we first need to find the vertex of the parabola. The vertex is the point where the function reaches its highest or lowest value. There are several methods to find the vertex, including using the vertex formula or completing the square. Once we have the coordinates of the vertex, we can determine whether it represents a maximum or minimum point.
A maximum point occurs when the coefficient of the quadratic term is negative, indicating that the parabola opens downwards. In this case, the vertex represents the highest point of the function. On the other hand, a minimum point occurs when the coefficient of the quadratic term is positive, indicating that the parabola opens upwards. In this case, the vertex represents the lowest point of the function.
Knowing the maximum and minimum points of a quadratic function is crucial in various real-life applications. For example, in the field of physics, these points can represent the maximum or minimum heights of objects thrown into the air, the maximum or minimum temperatures in a given time period, or the maximum or minimum distances traveled by a projectile. By analyzing the maximum and minimum points, we can make informed predictions and calculations.
In summary, the maximum and minimum points of a quadratic function provide valuable insights into its behavior and characteristics. They can be found by determining the vertex of the parabola and interpreting whether it represents a maximum or minimum point. Understanding these points allows us to make meaningful predictions and calculations in various real-life applications.
Solving Quadratic Equations Worksheet Answers
Quadratic equations are mathematical equations of the form ax^2 + bx + c = 0, where a, b, and c are constants. Solving quadratic equations involves finding the values of x that satisfy the equation. Quadratic equations can be solved using various methods, such as factoring, completing the square, or using the quadratic formula.
When working on a solving quadratic equations worksheet, the answers to the problems can be found by applying the appropriate method to each equation. For example, if the equation can be factored, the answer can be obtained by finding the values of x that make each factor equal to zero.
Another method for solving quadratic equations is by completing the square. This method involves rewriting the equation in the form (x – h)^2 = k, where h and k are constants. By solving for x in this form, the answers to the worksheet problems can be determined.
The quadratic formula, x = (-b ± √(b^2 – 4ac)) / 2a, is a commonly used method for solving quadratic equations. By substituting the values of a, b, and c into the formula, the solutions for x can be calculated. The answers for the worksheet problems can then be determined by plugging in the appropriate values.
In conclusion, a solving quadratic equations worksheet provides practice for solving quadratic equations using various methods, such as factoring, completing the square, and using the quadratic formula. By applying the appropriate method to each equation, the answers can be obtained. These methods allow for a systematic approach to solving quadratic equations and finding the values of x that satisfy the equation.