
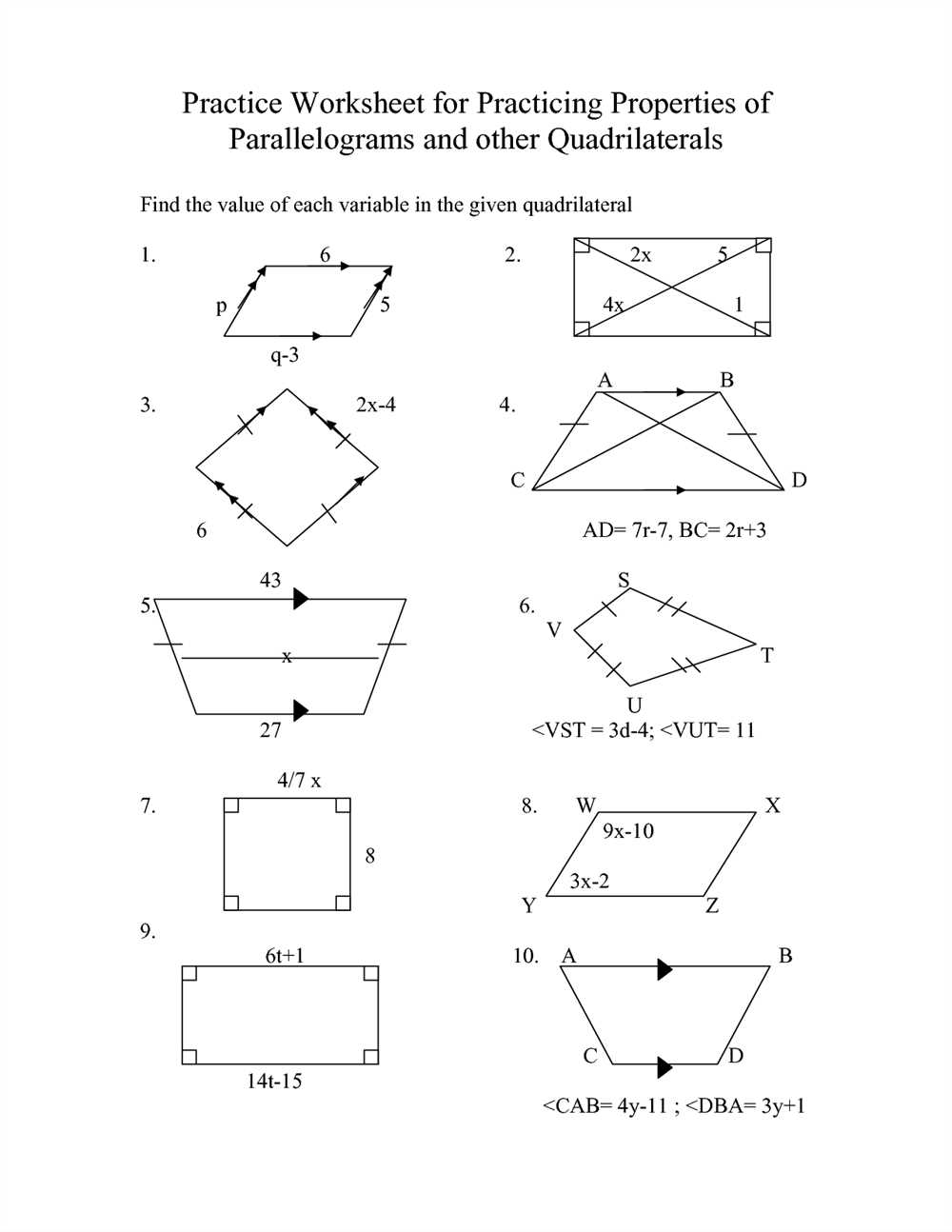
Proving that quadrilaterals are parallelograms is an important concept in geometry. It helps us understand the properties of quadrilaterals and their relationships with parallel lines. In this article, we will provide a worksheet with answers in PDF format that will help students practice proving quadrilaterals are parallelograms.
The worksheet consists of various exercises that require students to apply different theorems and properties of parallelograms. Each exercise provides a quadrilateral and some given information, and students are required to prove that the quadrilateral is a parallelogram using the given information. They will need to use the properties such as opposite sides being congruent, opposite angles being congruent, and diagonals bisecting each other.
This worksheet is designed to enhance students’ understanding and skills in proving quadrilaterals are parallelograms. By practicing these exercises, students will develop their logical thinking and deductive reasoning abilities. It will also deepen their understanding of the properties of parallelograms and their relationship with parallel lines.
The answers to each exercise are provided in the worksheet. This allows students to check their work and verify if their proofs are correct. It also serves as a useful tool for teachers to assess their students’ understanding and provide feedback.
In conclusion, the “Proving Quadrilaterals are Parallelograms Worksheet with Answers PDF” is a valuable resource for students studying geometry. It offers a variety of exercises that require the application of theorems and properties of parallelograms to prove that given quadrilaterals are parallelograms. By practicing these exercises, students can enhance their knowledge and skills in this fundamental concept of geometry.
Understanding Quadrilaterals
Quadrilaterals are polygons that have four sides and four angles. They are a fundamental concept in geometry and are used to describe and classify different shapes. Understanding the properties of quadrilaterals is essential in solving problems involving angles, lengths, and parallel lines.
There are different types of quadrilaterals, including rectangles, squares, parallelograms, and trapezoids. Each type has its own unique properties and characteristics.
Rectangles
A rectangle is a quadrilateral with four right angles. This means that all of its angles are 90 degrees. Additionally, opposite sides of a rectangle are parallel and congruent, and the diagonals bisect each other.
Squares
A square is a special type of rectangle where all four sides are congruent. This means that all angles of a square are also equal to 90 degrees. Like rectangles, squares have opposite sides that are parallel and congruent, and the diagonals bisect each other.
Parallelograms
A parallelogram is a quadrilateral with opposite sides that are parallel and congruent. This means that the opposite sides of a parallelogram never intersect and have the same length. In addition, opposite angles of a parallelogram are congruent, meaning they have the same measure.
Trapezoids
A trapezoid is a quadrilateral with only one pair of parallel sides. The other two sides are non-parallel and can have different lengths. The angles of a trapezoid can vary, but the two base angles are always congruent.
Understanding the properties of these different types of quadrilaterals is important in solving problems involving angles, lengths, and parallel lines. It allows mathematicians to classify and analyze shapes, making it easier to find solutions and prove theorems.
Properties and characteristics of quadrilaterals
A quadrilateral is a polygon with four sides and four vertices. Each quadrilateral has its own unique properties and characteristics that distinguish it from other polygons. Understanding these properties can help us identify and classify quadrilaterals.
1. Parallelograms:
A parallelogram is a quadrilateral with opposite sides that are parallel and equal in length. The opposite angles are also equal. This means that the opposite sides are congruent and the opposite angles are congruent. Additionally, the diagonals of a parallelogram bisect each other, meaning they divide each other into two equal segments.
2. Rectangles:
A rectangle is a parallelogram with all right angles. This means that all four angles of a rectangle are equal to 90 degrees. Additionally, the diagonals of a rectangle are congruent and bisect each other.
3. Squares:
A square is a rectangle with all sides of equal length. This means that all four sides of a square are congruent. Since a square is also a rectangle, it has all the properties of a rectangle, including congruent diagonals and right angles.
4. Trapezoids:
A trapezoid is a quadrilateral with one pair of parallel sides. The non-parallel sides are called the legs of the trapezoid, while the parallel sides are called the bases. The diagonals of a trapezoid do not have any specific properties.
5. Rhombuses:
A rhombus is a parallelogram with all sides of equal length. This means that all four sides of a rhombus are congruent. The opposite angles of a rhombus are also equal. Additionally, the diagonals of a rhombus bisect each other at right angles.
In conclusion, quadrilaterals can be classified into different types based on their properties and characteristics. These include parallelograms, rectangles, squares, trapezoids, and rhombuses. Understanding these properties can help us solve problems involving quadrilaterals and determine their specific classifications.
Proving quadrilaterals are parallelograms
In geometry, a quadrilateral is a polygon with four sides. A parallelogram is a special type of quadrilateral where opposite sides are parallel. There are several methods to prove that a given quadrilateral is a parallelogram.
Method 1: Using opposite sides
- Start by identifying the four sides of the quadrilateral.
- Measure the lengths of the opposite sides.
- If the opposite sides are equal in length, then the quadrilateral is a parallelogram.
Method 2: Using opposite angles
- Identify the four angles of the quadrilateral.
- Measure the measures of the opposite angles.
- If the opposite angles are equal in measure, then the quadrilateral is a parallelogram.
Method 3: Using diagonals
- Draw the diagonals of the quadrilateral, connecting the opposite vertices.
- If the diagonals bisect each other (i.e., they intersect at their midpoints), then the quadrilateral is a parallelogram.
Method 4: Using parallel sides
- Identify the four sides of the quadrilateral.
- If the opposite sides are parallel, then the quadrilateral is a parallelogram.
By using one or more of these methods, it is possible to prove that a given quadrilateral is a parallelogram. These proofs are important in geometry as they help establish the properties and relationships of various shapes and figures.
Definition of a parallelogram
A parallelogram is a special type of quadrilateral that has four sides and four angles. It is defined as a quadrilateral in which both pairs of opposite sides are parallel. This means that the opposite sides never intersect and are always equidistant from each other.
One of the key features of a parallelogram is its opposite sides. These sides are parallel and of equal length, making them congruent. This property makes it possible to prove that a quadrilateral is a parallelogram by showing that its opposite sides are parallel and congruent.
In addition to its opposite sides, a parallelogram also has opposite angles that are congruent. This means that the angles formed by the intersection of two adjacent sides are equal in measure. Additionally, the sum of the angles in a parallelogram is always equal to 360 degrees.
Some common examples of parallelograms include squares, rectangles, and rhombi. These are all special cases of parallelograms that have additional properties and characteristics.
In summary, a parallelogram is a quadrilateral with both pairs of opposite sides parallel and congruent. It also has opposite angles that are congruent and a sum of angles equal to 360 degrees. Understanding these properties and characteristics is essential for proving that a quadrilateral is a parallelogram.
Proving a Quadrilateral is a Parallelogram
When dealing with quadrilaterals, it is important to understand the properties of a parallelogram. A parallelogram is a special type of quadrilateral with four sides where opposite sides are equal in length and parallel to each other. To prove that a quadrilateral is a parallelogram, we can use various methods and properties.
One method is by proving that opposite sides are equal in length. If we can show that the lengths of the opposite sides of a quadrilateral are equal, we can conclude that it is a parallelogram. This can be done by measuring or by using given information about the quadrilateral’s properties. For example, if we know that the diagonals of the quadrilateral bisect each other, we can use that information to prove that opposite sides are equal.
Another method is by proving that opposite angles are congruent. If we can show that the measures of the opposite angles of a quadrilateral are equal, we can conclude that it is a parallelogram. This can be done by using angle relationships within the quadrilateral, such as alternate interior angles or corresponding angles. If we can prove that these angles are congruent, we can then conclude that the quadrilateral is a parallelogram.
In addition, we can also prove that a quadrilateral is a parallelogram by showing that one pair of opposite sides is both parallel and equal in length. If we can demonstrate that one pair of opposite sides meets these criteria, we can conclude that the quadrilateral is a parallelogram. This can be done by using geometric theorems or postulates, such as the opposite sides of a rectangle are parallel and equal in length.
Overall, proving that a quadrilateral is a parallelogram involves demonstrating that its properties align with those of a parallelogram, such as having equal opposite sides, congruent opposite angles, or parallel and equal opposite sides. By using these methods and properties, we can confidently prove whether a given quadrilateral is a parallelogram or not.
Methods for proving quadrilaterals
Proving that a quadrilateral is a parallelogram can be done using various methods and properties. One common approach is to show that both pairs of opposite sides are parallel. This can be done by using the fact that if the opposite sides of a quadrilateral are congruent, then the quadrilateral is a parallelogram. By measuring the lengths of the sides and showing their equality, one can establish that the quadrilateral is indeed a parallelogram.
Another method involves proving that both pairs of opposite angles are congruent. This can be done by using the fact that if the opposite angles of a quadrilateral are congruent, then the quadrilateral is a parallelogram. By measuring the angles and showing their equality, one can demonstrate that the quadrilateral meets the criteria for being a parallelogram.
Furthermore, showing that one pair of opposite sides is both parallel and congruent is also a valid way of proving that a quadrilateral is a parallelogram. This can be done by using the fact that if one pair of opposite sides of a quadrilateral is both parallel and congruent, then the quadrilateral is a parallelogram. By proving both the parallelism and congruence of the sides, one can establish the quadrilateral as a parallelogram.
Overall, these methods provide effective ways of proving that a quadrilateral is a parallelogram by using properties such as parallel sides and congruent angles. By carefully applying these properties and providing the necessary evidence, one can confidently conclude that a quadrilateral is indeed a parallelogram.
Theorems and Postulates for Proving Parallelograms
In geometry, a parallelogram is a quadrilateral with two pairs of parallel sides. Proving that a quadrilateral is a parallelogram requires the use of specific theorems and postulates that provide evidence of the parallel sides and other congruent angles and sides. By applying these theorems and postulates, mathematicians can establish the characteristics and properties of parallelograms.
1. The Consecutive Angles Theorem: If the consecutive angles of a quadrilateral are supplementary, then it is a parallelogram. This theorem states that if the sum of two consecutive angles in a quadrilateral is 180 degrees, then the opposite sides of the quadrilateral are parallel.
2. The Opposite Sides Theorem: If both pairs of opposite sides of a quadrilateral are congruent, then it is a parallelogram. This theorem states that if the opposite sides of a quadrilateral are equal in length, then the quadrilateral is a parallelogram.
3. The Diagonals Theorem: If the diagonals of a quadrilateral bisect each other, then it is a parallelogram. This theorem states that if the diagonals of a quadrilateral divide each other into equal segments, then the quadrilateral is a parallelogram.
4. The Opposite Angles Theorem: If both pairs of opposite angles of a quadrilateral are congruent, then it is a parallelogram. This theorem states that if the opposite angles in a quadrilateral are equal in measure, then the quadrilateral is a parallelogram.
These theorems and postulates provide the necessary tools for mathematicians to prove quadrilaterals are parallelograms. By examining the properties and relationships of angles, sides, and diagonals, geometric proofs can be constructed to demonstrate the parallel nature of a quadrilateral’s sides. These theorems and postulates form the foundation of parallelogram proofs and contribute to a deeper understanding of their properties.
Using angles and sides to prove quadrilaterals
When it comes to proving that a quadrilateral is a parallelogram, angles and sides play a crucial role in determining its properties. By examining the interior angles and the lengths of the sides, mathematicians can provide evidence to support their claims.
Angles: One way to prove that a quadrilateral is a parallelogram is by examining its angles. If opposite angles are congruent, that is, if they have the same measure, it indicates that the quadrilateral is a parallelogram. Additionally, if the consecutive interior angles are supplementary, meaning that they add up to 180 degrees, it further supports that the shape is a parallelogram.
Sides: Another aspect to consider when proving quadrilaterals is the lengths of their sides. If opposite sides of a quadrilateral are congruent, meaning they have the same length, it suggests that the shape is a parallelogram. Additionally, if the diagonals of the quadrilateral bisect each other, dividing them into two equal parts, it further supports the claim that the shape is a parallelogram.
Using these properties: By utilizing the properties of angles and sides, mathematicians can systematically analyze the characteristics of a quadrilateral and provide a logical proof that it is a parallelogram. This method allows for a clear and verifiable way of determining the nature of a given shape, which can be useful in various mathematical applications and problem-solving scenarios.