
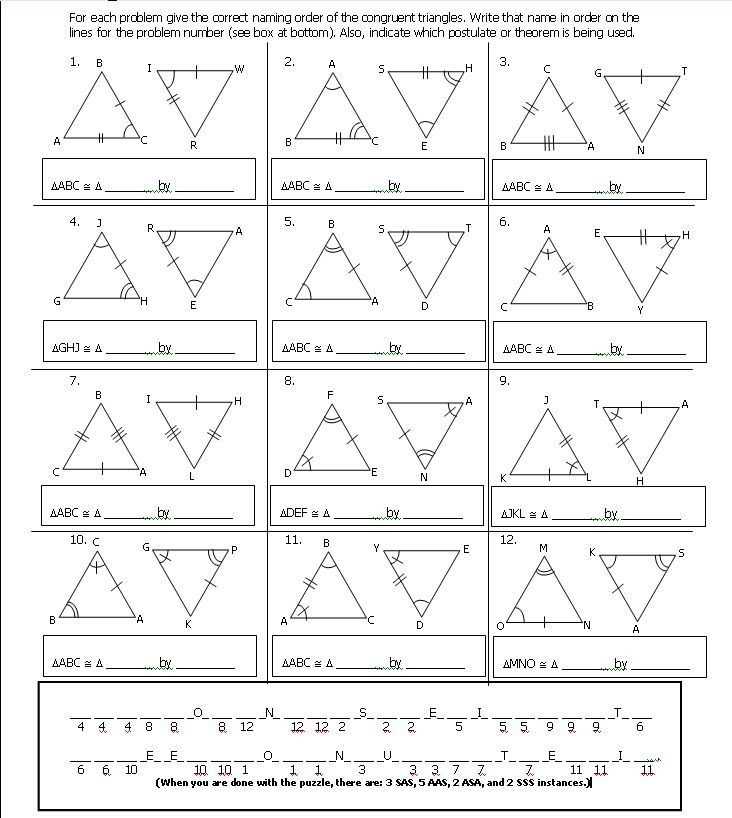
Proving triangles congruent is a fundamental concept in geometry. When we say that two triangles are congruent, it means that they have the same size and shape. In other words, if we were to take one triangle and move it, rotate it, or flip it, it would fit exactly on top of the other triangle.
Proving triangles congruent can be done using different methods and theorems. One common method is using the Side-Side-Side (SSS) congruence theorem. This theorem states that if three sides of one triangle are congruent to three sides of another triangle, then the two triangles are congruent.
Another method is using the Side-Angle-Side (SAS) congruence theorem. This theorem states that if two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the two triangles are congruent.
Proving triangles congruent is an important skill in geometry as it allows us to make deductions and solve problems involving triangles. By understanding the different methods and theorems for proving triangles congruent, we can unlock a powerful tool for analyzing and understanding geometric shapes.
Side-Side-Side (SSS) Congruence Postulate
The Side-Side-Side (SSS) Congruence Postulate is one of the ways to prove that two triangles are congruent. According to this postulate, if all three sides of one triangle are congruent to the corresponding sides of another triangle, then the two triangles are congruent.
To use the SSS Congruence Postulate, we need to identify three pairs of corresponding sides that are congruent. For example, if we have triangle ABC and triangle DEF, we need to show that AB is congruent to DE, BC is congruent to EF, and AC is congruent to DF.
We can use this postulate in various proofs and geometric problems. For example, if we are given two congruent triangles and one of the triangles has an additional side, we can use the SSS Congruence Postulate to prove that the two triangles are congruent.
The SSS Congruence Postulate is a powerful tool in geometry because it allows us to prove congruence without having to rely on angles. By simply comparing the lengths of the sides, we can determine if two triangles are congruent. This postulate is an essential concept in triangle congruence and lays the foundation for further geometric proofs and theorems.
Side-Angle-Side (SAS) Congruence Postulate
The Side-Angle-Side (SAS) Congruence Postulate states that if two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the triangles are congruent. In other words, if we have two triangles that have the same length for two sides and the same angle between them, then we can conclude that the triangles are congruent.
This theorem is based on the fact that if two triangles have the same lengths for two sides and the same angle between them, then all corresponding angles and sides of the triangles will be congruent. This helps us to prove that the two triangles are congruent without having to prove all six parts of the triangles separately.
When using the SAS Congruence Postulate to prove triangles congruent, it is important to follow the order of the sides and angles given. The order of the sides and angles must match in both triangles in order to apply the postulate. If the order is different, then we cannot conclude that the triangles are congruent using the SAS Congruence Postulate.
Overall, the SAS Congruence Postulate is a useful tool in proving triangles congruent. It allows us to focus on specific parts of the triangles and make conclusions about the congruence of the entire triangle. By using this postulate, we can simplify our proofs and save time in proving congruence.
Angle-Side-Angle (ASA) Congruence Postulate
The Angle-Side-Angle (ASA) Congruence Postulate is one of the ways to prove that two triangles are congruent. According to this postulate, if two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then the two triangles are congruent. In other words, if we have two triangles where the measures of two angles and the length of the side between them are equal, then the triangles are congruent.
To use the ASA Congruence Postulate, we need to find evidence that satisfies the given conditions. We can start by identifying two angles in one triangle that are congruent to two angles in the other triangle. Then, we can determine if the length of the side between these angles is also congruent. If all three conditions are met, we can conclude that the two triangles are congruent.
This postulate is based on the fact that if two angles of one triangle are congruent to two angles of another triangle, then the third angles must also be congruent since the sum of the angles in a triangle is always 180 degrees. Additionally, the included side must be congruent since the angles that form it are congruent.
Using the ASA Congruence Postulate, we can prove and establish the congruence of triangles in various geometric situations. This postulate is a helpful tool in solving problems and proving the congruence of triangles based on the given information.
Angle-Angle-Side (AAS) Congruence Postulate
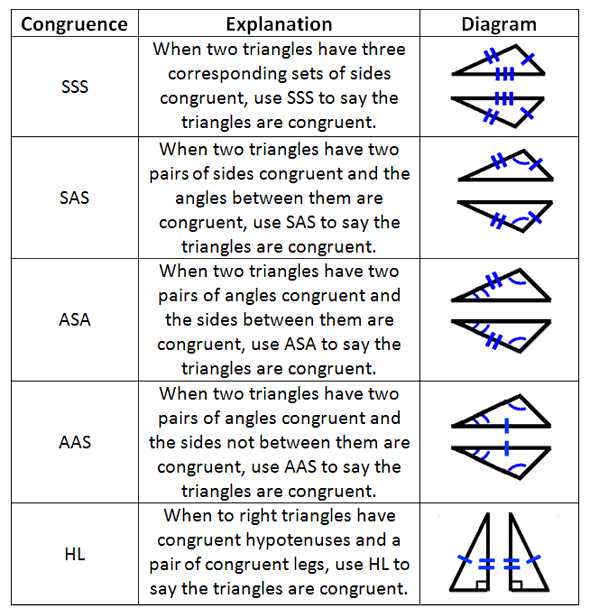
The Angle-Angle-Side (AAS) Congruence Postulate states that if two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then the two triangles are congruent.
In other words, if we have two triangles, and we know that two angles of one triangle are congruent to two angles of the other triangle, and the included side between these two angles is congruent as well, then we can conclude that the two triangles are congruent.
This postulate is based on the fact that triangles are closed figures, meaning that all the angles in a triangle must add up to 180 degrees. Therefore, if two angles of one triangle are congruent to two angles of another triangle, then the third angle of the first triangle must be congruent to the third angle of the second triangle in order to satisfy this property. Additionally, if the included side between the congruent angles is congruent as well, then the corresponding sides will also be congruent, completing the congruence between the two triangles.
The AAS Congruence Postulate is a useful tool in proving triangle congruence, as it allows us to establish the congruence of triangles based on a set of known angles and sides. By using this postulate, we can determine when two triangles are guaranteed to be congruent and apply it to solve various geometry problems and proofs.
Hypotenuse-Leg (HL) Congruence Postulate
The Hypotenuse-Leg (HL) Congruence Postulate is an important concept in geometry that explains when two right triangles are congruent. According to this postulate, if the hypotenuse and one leg of a right triangle are congruent to the hypotenuse and one leg of another right triangle, then the two triangles are congruent.
This postulate is based on the fact that if two sides and the included angle of a triangle are congruent to the corresponding sides and included angle of another triangle, then the two triangles are congruent. In the case of right triangles, the included angle is always 90 degrees, so we only need to compare the lengths of the hypotenuse and one leg.
For example, let’s say we have two right triangles, Triangle ABC and Triangle DEF. If we know that AB is congruent to DE and AC is congruent to DF, and both triangles have a right angle at points B and E respectively, then we can conclude that Triangle ABC is congruent to Triangle DEF using the HL Congruence Postulate.
This postulate is particularly useful in solving problems involving right triangles. By knowing the lengths of the hypotenuse and one leg of a triangle, we can determine the congruence of two triangles and make further deductions about their properties or measurements.
Corresponding Parts of Congruent Triangles Are Congruent (CPCTC)
The Corresponding Parts of Congruent Triangles Are Congruent (CPCTC) theorem is one of the most important results in triangle congruence. It states that if two triangles are congruent, then their corresponding parts are also congruent. This theorem allows us to make further deductions about the properties of congruent triangles.
For example, if we are given that triangle ABC is congruent to triangle DEF, we can conclude that angle A is congruent to angle D, side AB is congruent to side DE, and segment AC is congruent to segment DF. We can also deduce that the measures of the other angles and sides in the triangles are equal.
The CPCTC theorem is often used in a geometric proof to show the congruence of triangles. By establishing that all corresponding parts are congruent, we can prove that two triangles are congruent and use this information to solve other geometrical problems.
- In summary, the CPCTC theorem states that if two triangles are congruent, then their corresponding parts – angles, sides, and segments – are also congruent.
- This theorem allows us to make deductions and solve geometrical problems by establishing the congruence of triangles.
- The CPCTC theorem is fundamental in triangle congruence proofs and is used to show that two triangles are congruent.
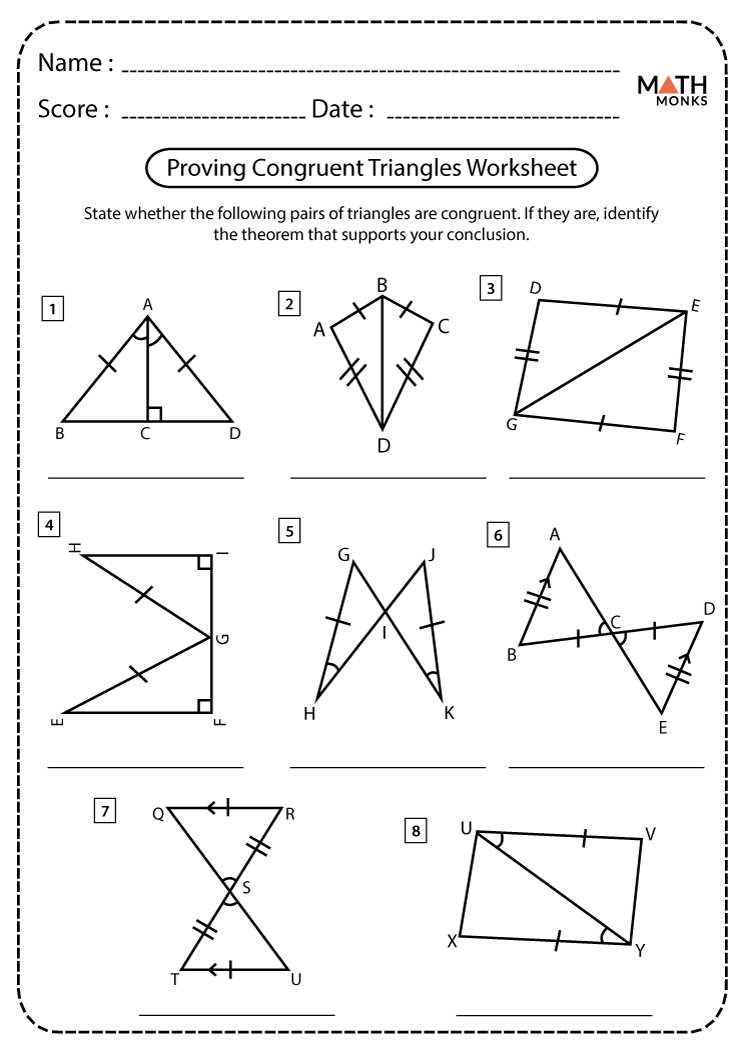
Triangle Congruence Proofs Examples
When it comes to proving that two triangles are congruent, there are several methods that can be used. One common method is using the congruence postulates and theorems, such as the Side-Side-Side (SSS) congruence theorem or the Angle-Angle-Side (AAS) congruence theorem. These theorems state that if certain conditions are met, the triangles are congruent. For example, if the lengths of the three sides of one triangle are equal to the lengths of the corresponding sides of another triangle, then the triangles are congruent by the SSS congruence theorem.
Let’s consider an example to better understand how these congruence proofs work. Given two triangles, triangle ABC and triangle DEF. We are given that AB = DE, BC = EF, and the measure of angle A is equal to the measure of angle D. To prove that triangle ABC is congruent to triangle DEF, we can use the AAS congruence theorem. According to the AAS congruence theorem, if two angles and a non-included side of one triangle are equal to the corresponding angles and non-included side of another triangle, then the triangles are congruent. In this case, we have angle A = angle D, side AB = side DE, and angle B = angle E (since they are corresponding angles). Therefore, we can conclude that triangle ABC is congruent to triangle DEF.
- Given: AB = DE, BC = EF, angle A = angle D
- Prove: triangle ABC congruent to triangle DEF
- Proof:
| Statements | Reasons |
|---|---|
| 1. AB = DE | Given |
| 2. BC = EF | Given |
| 3. angle A = angle D | Given |
| 4. triangle ABC has corresponding parts equal to triangle DEF | SSS congruence theorem |
| 5. triangle ABC congruent to triangle DEF | AAS congruence theorem |
In this example, we have used the given information and the AAS congruence theorem to prove that the two triangles are congruent. By following these logical steps, we can successfully prove the congruence of triangles using various congruence postulates and theorems.
Tips for Proving Triangles Congruent
Proving triangles congruent can be a challenging task, but with the right approach and strategy, it becomes manageable. Here are some useful tips to help you prove triangles congruent:
- Understand the congruence criteria: Familiarize yourself with the different criteria for proving triangle congruence such as SSS (side-side-side), SAS (side-angle-side), ASA (angle-side-angle), and AAS (angle-angle-side). Knowing these criteria will help you choose the appropriate method for proving triangle congruence.
- Identify corresponding parts: When comparing two triangles, it is essential to identify the corresponding parts such as sides and angles. By matching the corresponding parts, you can determine if the triangles are congruent or not.
- Use congruence postulates or theorems: Utilize the different postulates and theorems that establish triangle congruence. These include the Side-Angle-Side (SAS) Postulate, Angle-Side-Angle (ASA) Theorem, and Side-Side-Side (SSS) Postulate, among others. Choose the appropriate postulate or theorem based on the given information.
- Construct congruent triangles: If you are struggling to prove triangle congruence, consider constructing congruent triangles. Use tools such as a straightedge and compass to create triangles with the same sides and angles. This visual representation can make it easier to understand and prove triangle congruence.
- Provide clear and logical reasoning: When proving triangle congruence, it is important to provide clear and logical reasoning for each step. Clearly state the postulate or theorem being used and explain how the given information supports the congruence of the triangles.
- Review pre-requisite knowledge: Understanding the basic concepts of geometry, such as angle relationships, parallel lines, and properties of triangles, is crucial for proving triangle congruence. Ensure you have a solid foundation in these areas before attempting to prove triangles congruent.
- Practice with sample problems: The best way to improve your skills in proving triangle congruence is through practice. Solve a variety of sample problems that involve different congruence criteria and postulates. This will help you become familiar with the process and develop your problem-solving abilities.
By following these tips and practicing regularly, you can become proficient in proving triangles congruent. Remember to approach each problem with patience, attention to detail, and a logical mindset.