
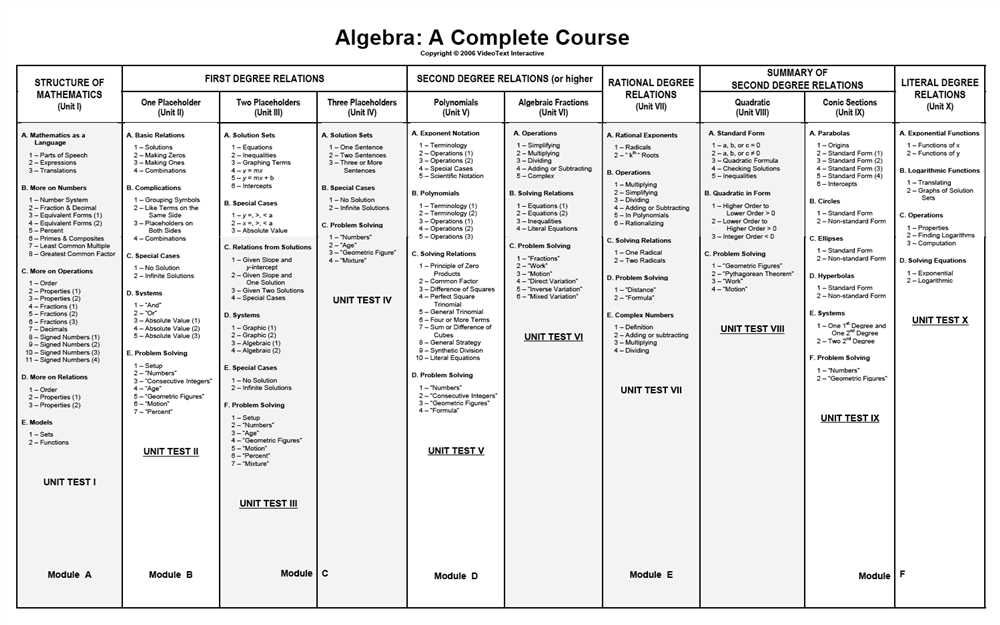
In mathematics, quadratic relations and conic sections play a significant role in understanding and solving various problems. From graphing parabolas to finding the equation of an ellipse, these concepts form a fundamental part of algebra and geometry. To test your understanding and mastery of these topics, teachers often administer a unit test specifically focused on quadratic relations and conic sections.
This unit test typically assesses your knowledge and skills in identifying and graphing different types of conic sections, such as parabolas, ellipses, and hyperbolas. It may include questions on finding the vertex, directrix, focus, and axis of symmetry of a given parabola, as well as determining the shape and orientation of an ellipse or hyperbola.
Additionally, the test may involve solving quadratic equations using different methods, such as factoring, completing the square, or using the quadratic formula. It may also require you to apply your knowledge of quadratic relations and conic sections to real-world problems, such as finding the maximum or minimum value of a quadratic function or determining the trajectory of a projectile.
Preparing for a quadratic relations and conic sections unit test requires a solid understanding of the formulas, properties, and graphical representations associated with these concepts. It is important to review the fundamental principles, practice solving various types of problems, and familiarize yourself with the different types of conic sections and their unique characteristics. By studying effectively and thoroughly preparing for the test, you will be well-equipped to demonstrate your knowledge and skills in quadratic relations and conic sections.
Quadratic Relations and Conic Sections Unit Test
The Quadratic Relations and Conic Sections Unit Test is designed to assess your understanding of quadratic equations, conic sections, and their properties. This test is an important part of the curriculum and will evaluate your knowledge and skills in this topic.
The test will cover topics such as graphing quadratic equations, solving quadratic equations by factoring, completing the square, and the quadratic formula. You will also be tested on your ability to identify and graph different types of conic sections, including circles, ellipses, parabolas, and hyperbolas.
The test will include both multiple-choice questions and open-ended questions. You will need to demonstrate your understanding of the concepts and be able to apply them to solve problems. It is important to review your notes, textbook, and any class materials to prepare for the test.
During the test, make sure to read each question carefully and thoroughly. Pay attention to any given information or clues that can help you solve the problem. Show all your work and provide clear explanations for your answers.
Remember that practice is key to success in mathematics. Take the time to review the concepts, practice solving quadratic equations and graphing conic sections, and seek help if needed. Good luck on your Quadratic Relations and Conic Sections Unit Test!
Understanding Quadratic Relations
A quadratic relation is a mathematical relationship between two variables, in which one variable is a function of the square of the other variable. It can be represented by a quadratic equation, which has the form y = ax^2 + bx + c, where a, b, and c are constants. The graph of a quadratic relation is a parabola.
Quadratic relations have various applications in real life, such as in physics, engineering, and economics. They can be used to model and analyze different situations, such as the trajectory of a projectile, the shape of a satellite dish, or the profit function of a business.
When studying quadratic relations, it is important to understand the key features of a quadratic equation, such as the vertex, axis of symmetry, and roots. The vertex is the highest or lowest point on the graph of a parabola, and it can be found using the formula x = -b/2a. The axis of symmetry is a vertical line that passes through the vertex, dividing the parabola into two symmetric halves. The roots, or solutions, of a quadratic equation are the values of x that make y equal to zero.
- Vertex: The highest or lowest point on the graph of a parabola.
- Axis of Symmetry: A vertical line that passes through the vertex, dividing the parabola into two symmetric halves.
- Roots/Solutions: The values of x that make y equal to zero.
By understanding these key features, one can analyze and interpret the behavior of quadratic relations, make predictions, and solve real-world problems. It is also important to be familiar with different forms of quadratic equations, such as factored form and vertex form, as they can provide different insights into the relationship between the variables.
In summary, understanding quadratic relations is crucial for various applications in different fields. By studying the key features and properties of quadratic equations, one can gain valuable insights into the behavior and dynamics of these relations, and apply them to practical situations for analysis and problem-solving.
Properties of Quadratic Functions
A quadratic function is a function that can be written in the form f(x) = ax^2 +bx+c, where a, b, and c are constants and a ≠ 0. Quadratic functions have many interesting properties that make them important in various fields of mathematics.
Vertex: One of the key properties of a quadratic function is the location of its vertex. The vertex is the point where the function reaches its maximum or minimum value. For a quadratic function in standard form, the vertex can be found using the formula (-b/2a, f(-b/2a)). The y-coordinate of the vertex represents the maximum or minimum value of the function, depending on the shape of the parabola.
Axis of Symmetry: Another important property of quadratic functions is the axis of symmetry. The axis of symmetry is a vertical line that passes through the vertex and divides the parabola into two equal halves. The equation of the axis of symmetry can be found using the formula x = -b/2a.
Intercepts: Quadratic functions can have x-intercepts and y-intercepts. The x-intercepts, also known as zeros or roots, are the points where the graph of the function intersects the x-axis. They can be found by setting the function equal to zero and solving for x. The y-intercept is the point where the graph intersects the y-axis. It can be found by evaluating the function at x = 0.
Concavity: The concavity of a quadratic function determines the shape of its graph. If the leading coefficient (a) is positive, the parabola opens upward and the function is concave up. If the leading coefficient is negative, the parabola opens downward and the function is concave down.
Maximum or Minimum Value: The maximum or minimum value of a quadratic function can be found by evaluating the function at the x-coordinate of the vertex. If the parabola opens upward, the vertex represents the minimum value of the function. If the parabola opens downward, the vertex represents the maximum value of the function.
Understanding the properties of quadratic functions is essential for analyzing and solving various real-world problems. These functions can model a wide range of phenomena, such as projectile motion, optimization, and patterns in nature. By studying the properties of quadratic functions, we can gain insight into the behavior and characteristics of these mathematical objects.
Solving Quadratic Equations

Quadratic equations are second-degree polynomial equations that can be written in the form ax^2 + bx + c = 0, where a, b, and c are constants. Solving quadratic equations involves finding the values of x that satisfy the equation.
There are several methods for solving quadratic equations, including factoring, the quadratic formula, and completing the square. Factoring is the process of breaking down the quadratic equation into two binomial factors. The quadratic formula is a general formula that can be used to find the roots of any quadratic equation. Completing the square involves transforming the quadratic equation into a perfect square trinomial.
- Factoring: To solve a quadratic equation by factoring, we look for two numbers that multiply to give the constant term c and add up to give the coefficient of the middle term b.
- Quadratic Formula: The quadratic formula is derived from completing the square and can be used to find the solutions of any quadratic equation.
- Completing the Square: Completing the square is a method used to transform a quadratic equation into a perfect square trinomial, which can then be easily solved to find the solutions.
Once we have found the solutions of a quadratic equation, we can use them to graph the equation on a coordinate plane and analyze its properties such as the vertex, axis of symmetry, and whether it opens upwards or downwards. Quadratic equations are also used in real-life situations, such as modeling the trajectory of a projectile or determining the maximum profit in a business.
Overall, solving quadratic equations is an important skill in algebra and has various real-world applications. Understanding different methods of solving quadratic equations allows us to find solutions accurately and efficiently.
Graphing Quadratic Functions
A quadratic function is a mathematical function of the form f(x) = ax^2 + bx + c, where a, b, and c are constants. Graphing quadratic functions allows us to visualize the shape and behavior of these functions. It helps us understand how the function changes as the input variable, x, varies.
To graph a quadratic function, we first need to identify its key features, such as the vertex, axis of symmetry, and the y-intercept. The vertex of a quadratic function can be found using the formula x = -b/2a, and then substituting x into the function to find the corresponding y-coordinate. The axis of symmetry is a vertical line that passes through the vertex and divides the graph into two symmetrical halves. The y-intercept is the point where the graph intersects the y-axis, which can be found by substituting x = 0 into the function.
Once we have the key features, we can plot points on the coordinate plane and draw a smooth curve that connects them. The shape of the graph depends on the value of the coefficient a. If a is positive, the graph opens upwards and has a minimum point at the vertex. If a is negative, the graph opens downwards and has a maximum point at the vertex. The steepness of the graph is determined by the value of a.
It is also helpful to find the x-intercepts of the quadratic function, which are the points where the graph intersects the x-axis. To find these points, we need to solve the equation f(x) = 0. Depending on the discriminant (b^2 – 4ac), there can be either two, one, or no x-intercepts. These x-intercepts, along with the vertex and y-intercept, provide a complete picture of the quadratic function’s graph.
Types of Conic Sections
Conic sections are the curves that result from the intersection of a plane and a cone. There are four main types of conic sections: circles, ellipses, parabolas, and hyperbolas. These curves have distinct shapes and properties that make them important in various fields of mathematics and science.
Circles are conic sections where the plane intersects the cone at a right angle to its axis. A circle is a set of points equidistant from its center, forming a closed curve. Circles have many applications in geometry, such as calculating the circumference, area, and angles within the circle.
Ellipses are conic sections where the plane intersects the cone at an angle that is less than a right angle to its axis. An ellipse is a set of points where the sum of the distances from any point on the curve to two fixed points (called the foci) is constant. Ellipses have various applications in physics, astronomy, and engineering, such as describing the orbits of planets and satellites.
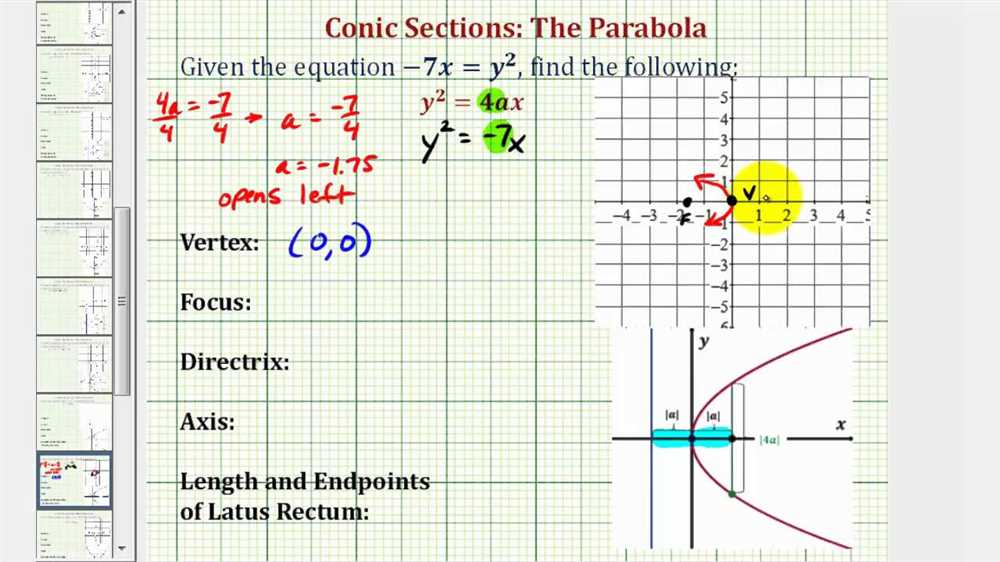
Parabolas are conic sections where the plane intersects the cone parallel to one of its sides. A parabola is a U-shaped curve that is symmetric with respect to its directrix and focus. Parabolas have practical uses in optics, engineering, and physics, such as in designing satellite dishes and reflecting telescopes.
Hyperbolas are conic sections where the plane intersects the cone at an angle that is greater than a right angle to its axis. A hyperbola is a set of points where the difference of the distances from any point on the curve to two fixed points (called the foci) is constant. Hyperbolas have applications in physics, engineering, and architecture, such as in designing satellite communication systems and cooling tower structures.
In summary, circles, ellipses, parabolas, and hyperbolas are the four main types of conic sections. Each has its own distinct shape and properties that make them useful in various fields of mathematics and science. Understanding these conic sections is crucial for solving problems and analyzing real-world phenomena.
Equations of Conic Sections
Conic sections are curves that can be formed by intersecting a plane with a double-napped cone. There are four types of conic sections: circles, ellipses, parabolas, and hyperbolas. Each type has its own unique equation that describes its shape and characteristics.
The equation of a circle is (x – h)^2 + (y – k)^2 = r^2, where (h, k) represents the center of the circle and r represents the radius. This equation tells us that all points (x, y) that satisfy this equation are equidistant from the center of the circle.
An ellipse is defined by the equation ((x – h)^2)/a^2 + ((y – k)^2)/b^2 = 1, where (h, k) represents the center of the ellipse, a represents the length of the major axis, and b represents the length of the minor axis. This equation tells us that the sum of the distances from any point on the ellipse to the two foci is constant.
A parabola can be described by the equation y = ax^2 + bx + c. This equation tells us that the parabola is symmetric with respect to its axis of symmetry, which is the line x = -b/2a. The coefficient a determines whether the parabola opens upwards or downwards.
A hyperbola is defined by the equation ((x – h)^2)/a^2 – ((y – k)^2)/b^2 = 1. This equation tells us that the absolute difference of the distances from any point on the hyperbola to the two foci is constant.
In summary, the equations of conic sections allow us to describe and analyze the properties of these curves. They provide valuable information about their shape, center, axes, and foci, which can be used to solve various problems in geometry and physics.