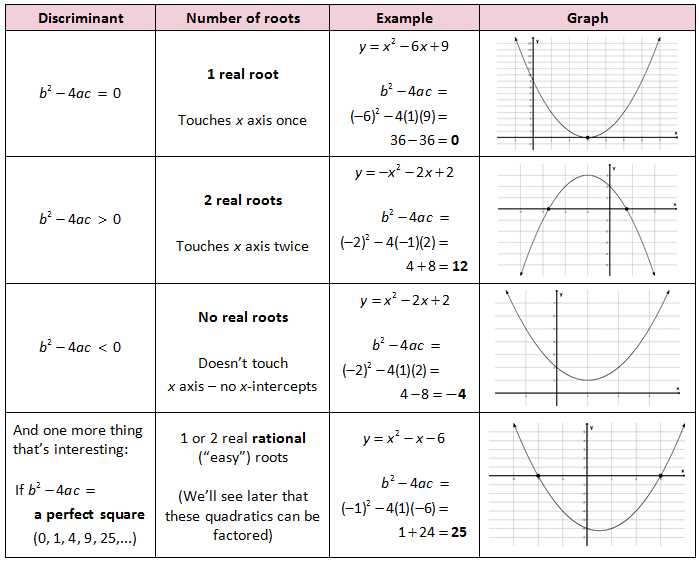
Quadratic equations are an essential part of algebra, and understanding their transformations is crucial for mastering this topic. To help students practice and test their understanding, quadratic transformations worksheets are a valuable resource. These worksheets provide various equations and ask students to identify the type of transformation applied to each equation and its corresponding effect on the graph.
Answering these worksheets is not just about memorizing a set of rules. It requires a deep understanding of how each transformation affects the quadratic equation and its graph. Students will need to analyze the equation and recognize how changes in the coefficients impact the parabola’s vertex, axis of symmetry, and direction of opening.
Quadratic transformations worksheets provide a wide range of equations, including those with translations, reflections, stretches, and compressions. Students must use their knowledge of quadratic functions to identify the specific type of transformation and describe its effect on the parabola. These worksheets also help students gain confidence in graphing equations and improve their problem-solving skills.
Quadratic Transformations Worksheet Answers
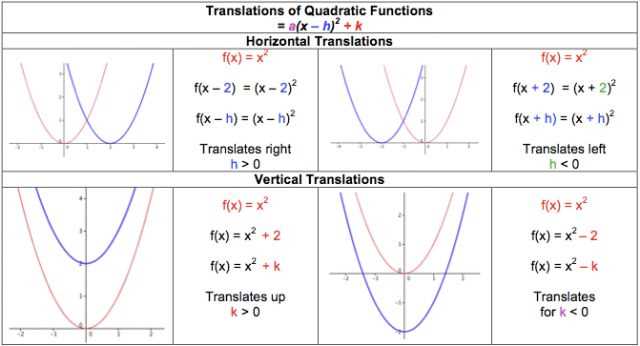
The quadratic transformations worksheet answers provide students with a comprehensive understanding of how quadratic functions can be transformed. By completing the worksheet, students are able to practice their skills in identifying the effects of different transformations on the vertex form of a quadratic equation.
This worksheet answers a variety of questions related to quadratic transformations, including finding the vertex, identifying whether the graph opens up or down, determining the value of “a” in the vertex form equation, and identifying translations in the x- and y-directions. The answers not only provide the final solutions but also explain the steps taken to arrive at the answer, allowing students to better understand the concepts behind the transformations.
By analyzing the answers provided, students can begin to recognize patterns and make connections between the different transformations. They can also check their own work and identify any errors they may have made. This worksheet is an essential tool for reinforcing the concepts of quadratic transformations and helping students build a strong foundation in quadratic functions and equations.
Overall, the quadratic transformations worksheet answers serve as a valuable resource for students studying quadratic functions. They provide clear explanations and examples that help students grasp the concepts of transformations and apply them to solving problems. With this worksheet, students can deepen their understanding of quadratic functions and gain confidence in their ability to manipulate and analyze quadratic equations.
Describing the Basic Quadratic Transformations
Quadratic transformations are changes made to the basic shape of a quadratic function. These transformations include translations, reflections, stretches, and compressions. Understanding these transformations is essential for analyzing and graphing quadratic functions.
Translation: A translation shifts the graph of a quadratic function vertically or horizontally. When a quadratic function is translated horizontally, the entire graph moves left or right, while keeping the same shape. When a quadratic function is translated vertically, the graph moves up or down, while maintaining the same width.
- A translation of (h, 0) horizontally shifts the graph by h units to the right if h > 0, or to the left if h < 0.
- A translation of (0, k) vertically shifts the graph by k units up if k > 0, or down if k < 0.
Reflection: A reflection flips the graph of a quadratic function across a line. When a quadratic function is reflected across the x-axis, the positive and negative values of the function are reversed. Similarly, when a quadratic function is reflected across the y-axis, the x-values are negated.
Stretches and Compressions: Stretches and compressions change the width and height of a quadratic function’s graph. A stretch makes the graph narrower and taller, while a compression makes the graph wider and shorter.
- A stretch or compression factor of a multiplies the x-values by a, and the y-values by a2.
- A stretch or compression factor of 1/a multiplies the x-values by 1/a, and the y-values by 1/a2.
By understanding and applying these basic quadratic transformations, students can manipulate and analyze quadratic functions with more precision and efficiency. This knowledge is valuable for solving real-world problems and mastering more advanced mathematical concepts.
Reflecting a Quadratic Function
A quadratic function is a function of the form $f(x) = ax^2 + bx + c$, where $a$, $b$, and $c$ are constants. Reflecting a quadratic function involves changing the sign of the coefficient $a$, which affects the shape of the graph.
When the coefficient $a$ is positive, the graph of the quadratic function opens upward and has a minimum point. On the other hand, when the coefficient $a$ is negative, the graph opens downward and has a maximum point.
To reflect a quadratic function, we can multiply the coefficient $a$ by $-1$ to change its sign. This transformation flips the graph over the x-axis, resulting in a new graph that is a mirror image of the original.
For example, let’s consider the quadratic function $f(x) = x^2 + 2x – 3$. The graph of this function opens upward. If we reflect it by multiplying the coefficient $a$ by $-1$, we get $g(x) = -x^2 – 2x + 3$. The graph of $g(x)$ opens downward and is a mirror image of $f(x)$.
Reflecting a quadratic function can be useful in various applications, such as optimizing a business model or analyzing the trajectory of a projectile. By understanding how reflections affect the shape of a quadratic graph, we can gain insights into the behavior of the function and make informed decisions based on the data.
Translating a Quadratic Function
A quadratic function is a function that can be written in the form f(x) = ax^2 + bx + c, where a, b, and c are constants. To translate a quadratic function, we can use transformations such as shifting it horizontally or vertically, reflecting it, or stretching or compressing it.
Horizontal Translation: To horizontally translate a quadratic function, we add or subtract a constant value to the x-values of the function. For example, if we have the function f(x) = x^2 and we want to shift it 2 units to the right, we can write it as g(x) = (x – 2)^2. Similarly, to shift it 3 units to the left, we can write it as h(x) = (x + 3)^2.
Vertical Translation: To vertically translate a quadratic function, we add or subtract a constant value to the y-values of the function. For example, if we have the function f(x) = x^2 and we want to shift it 4 units up, we can write it as g(x) = x^2 + 4. Similarly, to shift it 5 units down, we can write it as h(x) = x^2 – 5.
Reflection: To reflect a quadratic function, we change the sign of the coefficient of x in the function. For example, if we have the function f(x) = -x^2, the reflection of this function would be g(x) = x^2.
Stretching/Compressing: To stretch or compress a quadratic function, we change the value of coefficient a in the function. If a > 1, the graph will be stretched vertically, and if 0 < a < 1, the graph will be compressed vertically. For example, if we have the function f(x) = 2x^2, the graph will be stretched vertically and narrower compared to the graph of the function g(x) = x^2. On the other hand, if we have the function h(x) = 0.5x^2, the graph will be compressed vertically and wider compared to the graph of the function g(x) = x^2.
Stretching or Shrinking a Quadratic Function
A quadratic function is a type of polynomial function that has a degree of 2. It has the general form of f(x) = ax^2 + bx + c, where a, b, and c are constants.
When we talk about stretching or shrinking a quadratic function, we are referring to changes made to the graph of the function. These changes can be made by multiplying the function by a constant.
To stretch a quadratic function horizontally, we can multiply the x-values by a constant greater than 1. This will make the graph narrower and taller. For example, if we have the equation f(x) = 2x^2, the graph will be wider and shorter compared to the original graph of f(x) = x^2.
To shrink a quadratic function horizontally, we can multiply the x-values by a constant between 0 and 1. This will make the graph wider and shorter. For example, if we have the equation f(x) = (1/2)x^2, the graph will be narrower and taller compared to the original graph of f(x) = x^2.
To stretch a quadratic function vertically, we can multiply the entire function by a constant greater than 1. This will make the graph taller and narrower. For example, if we have the equation f(x) = x^2, the graph will be shorter and wider compared to the original graph of f(x) = (1/2)x^2.
To shrink a quadratic function vertically, we can multiply the entire function by a constant between 0 and 1. This will make the graph shorter and wider. For example, if we have the equation f(x) = 2x^2, the graph will be taller and narrower compared to the original graph of f(x) = x^2.
By understanding how to stretch or shrink a quadratic function, we can manipulate the graph to fit different purposes and analyze different scenarios.
Combining Quadratic Transformations
When studying quadratic transformations, it can be useful to combine multiple transformations in a single equation. By combining translations, reflections, stretches, and compressions, we can create complex quadratic functions that can be used to model various real-life situations.
Let’s start by reviewing the basic quadratic function equation: y = ax^2 + bx + c. Here, a determines the direction of the graph’s opening, b affects the symmetry, and c is the vertical shift.
To add a horizontal shift to the graph, we can modify the equation using the transformation x → x – h, where h represents the magnitude of the shift. This moves the graph h units to the right if h is positive, or to the left if h is negative.
A vertical shift can be achieved by adding or subtracting a constant value to the equation. For example, to shift the graph up by k units, we modify the equation as y = ax^2 + bx + c + k. Positive values of k shift the graph up, while negative values shift it down.
We can also stretch or compress the graph by multiplying the quadratic equation by a constant value. If we multiply by a > 1, the graph is vertically stretched, while 0 < a < 1 results in a vertical compression. This affects the width and height of the graph.
By combining these transformations, we can create complex quadratic equations that accurately represent real-world data and phenomena. Understanding how these transformations work together is crucial for anyone studying quadratic functions and their applications.
Applying Quadratic Transformations to Real-World Problems
The study of quadratic transformations involves manipulating and graphing quadratic functions. This mathematical concept has practical applications in real-world scenarios, such as physics, engineering, and economics. By understanding how to apply these transformations, individuals can solve a variety of problems that involve quadratic relationships.
One example where quadratic transformations are applicable is in projectile motion. When an object is launched into the air, its trajectory can be modeled by a quadratic function. By understanding how to manipulate the function, such as changing the vertex or stretching the parabola, one can predict the object’s path and optimize its launch angle for maximum range or height.
Another real-world situation where quadratic transformations are useful is in cost-volume-profit analysis. In business, understanding the relationship between costs, volume, and profit is crucial for making informed decisions. By modeling these relationships as quadratic functions and applying transformations, individuals can analyze different scenarios and determine the most profitable course of action.
Overall, the ability to apply quadratic transformations to real-world problems is essential for problem-solving and decision-making in various fields. By understanding how to manipulate quadratic functions, individuals can analyze and optimize real-world scenarios, ultimately leading to improved outcomes and greater efficiency.
Quadratic Transformations Worksheet Answers
Understanding quadratic transformations is an important concept in algebra. By examining and analyzing quadratic functions, students can gain a deeper understanding of how changes in the equation can affect the graph of the function. The Quadratic Transformations Worksheet provides students with a set of quadratic functions and asks them to identify the type of transformation that has occurred.
The answers to the Quadratic Transformations Worksheet are valuable tools for students to check their work and ensure they have correctly identified the type of transformation. The worksheet may include various types of transformations, such as translations, reflections, stretches, and compressions. By comparing the original function to the transformed equation, students can determine the specific changes that have occurred.
- Translation: A translation occurs when the graph of the function is shifted horizontally or vertically. This can be identified by comparing the vertex of the original function to the vertex of the transformed equation.
- Reflection: A reflection occurs when the graph of the function is flipped across an axis. This can be identified by comparing the sign of the coefficient of the quadratic term in the original function to the transformed equation.
- Stretch: A stretch occurs when the graph of the function is vertically or horizontally stretched. This can be identified by comparing the coefficient of the quadratic term in the original function to the transformed equation.
- Compression: A compression occurs when the graph of the function is vertically or horizontally compressed. This can be identified by comparing the coefficient of the quadratic term in the original function to the transformed equation.
By using the Quadratic Transformations Worksheet answers, students can gain confidence in their ability to identify and understand the different types of transformations that can occur in quadratic functions. This knowledge is essential for further studies in algebra and calculus, as well as in practical applications of quadratic functions in areas such as physics and engineering.