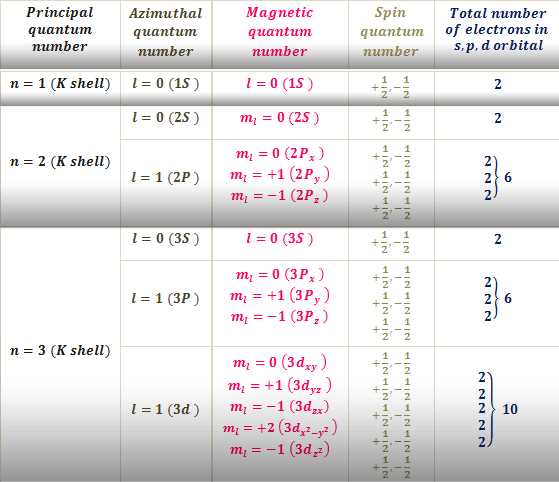
If you are studying quantum mechanics, it is essential to understand the concept of quantum numbers. Quantum numbers are values that describe the unique properties of an electron in an atom. These numbers determine the energy level, shape, orientation, and spin of an electron.
Practicing quantum numbers problems is crucial to developing a solid understanding of this fundamental concept. To help you in your studies, we have compiled a collection of quantum numbers practice problems with answers in a PDF format. This resource will allow you to test your knowledge and strengthen your skills in determining quantum numbers.
The practice problems in this PDF cover various aspects of quantum numbers, including the principal quantum number, azimuthal quantum number, magnetic quantum number, and spin quantum number. Each problem presents a scenario or description of an electron’s characteristics, and your task is to determine the appropriate quantum numbers that correspond to these characteristics.
By working through these practice problems, you will gain confidence in identifying and assigning quantum numbers correctly. This skill is essential for accurately describing electron configurations and understanding the behavior of electrons in atoms. Download the quantum numbers practice problems with answers PDF and enhance your understanding of this fascinating field of study.
Quantum Numbers Practice Problems with Answers PDF
Quantum numbers play a crucial role in understanding the electronic structure of atoms and molecules. They provide important information about the energy levels and spatial distribution of electrons. To master the concept of quantum numbers, it is essential to practice solving problems.
In this Quantum Numbers Practice Problems with Answers PDF, you will find a collection of problems that will test your understanding of quantum numbers. Each problem is designed to cover different aspects of quantum numbers, including the principal quantum number (n), azimuthal quantum number (l), magnetic quantum number (ml), and spin quantum number (ms).
Here is a sample problem from the Quantum Numbers Practice Problems with Answers PDF:
Problem:
What are the possible values of the azimuthal quantum number (l) for an electron in a 2p orbital?
Solution:
The azimuthal quantum number (l) represents the shape of the atomic orbital. For the 2p orbital, the possible values of (l) are 1 and 0. Since the 2p orbital corresponds to the second energy level (n = 2), it can have two different orientations, which are represented by the values of (l).
By practicing problems like these, you will enhance your understanding of quantum numbers and their significance in determining the electronic configuration of atoms and molecules. To access the complete set of Quantum Numbers Practice Problems with Answers in PDF format, download the file below.
Download Quantum Numbers Practice Problems with Answers PDF
What are Quantum Numbers

Quantum numbers are a set of values that describe the properties of an atomic or subatomic particle. They are used to determine the energy levels, orbital shapes, and orientations of electrons within an atom or molecule. Quantum numbers provide a way to uniquely identify and describe the behavior of particles in quantum mechanics.
There are four main quantum numbers that are used to describe an electron in an atom:
- Principal quantum number (n): This quantum number determines the energy level of an electron and indicates the distance of the electron from the nucleus. This value can be any positive integer starting from 1.
- Azimuthal quantum number (ℓ): This quantum number determines the shape of the orbital in which the electron is found. It can have values ranging from 0 to (n-1), where n is the principal quantum number.
- Magnetic quantum number (mℓ): This quantum number determines the orientation of the orbital in three-dimensional space. It can have integer values ranging from -ℓ to ℓ.
- Spin quantum number (ms): This quantum number describes the spin of the electron. It can have values of +1/2 or -1/2, indicating the two possible spin states of the electron.
To understand and predict the behavior of electrons in atoms and molecules, it is essential to know and apply the concepts of quantum numbers. They allow scientists to determine the arrangement of electrons and their energy levels, resulting in a better understanding of chemical bonding and the properties of matter at the atomic and subatomic levels.
Main Quantum Numbers

The main quantum numbers used in atomic physics are the principal quantum number (n), the orbital quantum number (l), the magnetic quantum number (ml), and the spin quantum number (ms).
The principal quantum number (n) describes the energy level or shell of an electron in an atom. It can have integer values ranging from 1 to infinity. The higher the value of n, the higher the energy level of the electron. For example, an electron in the first energy level (n=1) is closest to the nucleus, while an electron in the second energy level (n=2) is further away.
The orbital quantum number (l) determines the shape of the orbital. It can have values ranging from 0 to (n-1) for each energy level. The values correspond to different subshells: s (l=0), p (l=1), d (l=2), f (l=3), and so on. The s subshell is spherical, the p subshell is dumbbell-shaped, and so on.
The magnetic quantum number (ml) specifies the orientation of the orbital in space. It can have integer values ranging from -l to +l. For example, in the p subshell (l=1), the values of ml can be -1, 0, or +1, corresponding to the three p orbitals oriented along the x, y, and z axes.
The spin quantum number (ms) describes the intrinsic spin of the electron. It can have values of +1/2 or -1/2, indicating the two possible spin states of an electron within an orbital.
| Main Quantum Number | Description/Range | |
|---|---|---|
| n | Principal quantum number | 1 to infinity |
| l | Orbital quantum number | 0 to (n-1) |
| ml | Magnetic quantum number | -l to +l |
| ms | Spin quantum number | +1/2 or -1/2 |
Angular Momentum Quantum Number
The angular momentum quantum number (l) is one of the four quantum numbers used to describe the properties of an electron in an atom. It describes the shape of the orbital and determines the possible values of the azimuthal (angular) quantum number (m). The values of l range from 0 to (n-1), where n is the principal quantum number.
The angular momentum quantum number can be visualized as the number of orbitals that an electron can occupy within a given principal energy level. Each value of l corresponds to a different subshell within a given energy level. For example, when l=0, the subshell is called s; when l=1, the subshell is called p; when l=2, the subshell is called d; and when l=3, the subshell is called f. The s subshell has only one orbital, the p subshell has three orbitals, the d subshell has five orbitals, and the f subshell has seven orbitals.
For each value of l, there are 2l+1 possible values of m, which represent the orientation of the orbital in three-dimensional space. The m values range from -l to +l. For example, when l=1, there are three possible values of m (-1, 0, +1), which correspond to the three p orbitals.
- Example: For an electron in the 3rd energy level (n=3), the possible values of l are 0, 1, and 2. This means that there are three subshells within the 3rd energy level: s, p, and d. The s subshell has one orbital, the p subshell has three orbitals, and the d subshell has five orbitals.
- Example: For an electron in the 4th energy level (n=4), the possible values of l are 0, 1, 2, and 3. This means that there are four subshells within the 4th energy level: s, p, d, and f. The s subshell has one orbital, the p subshell has three orbitals, the d subshell has five orbitals, and the f subshell has seven orbitals.
The angular momentum quantum number plays a crucial role in determining the energy, shape, and orientation of an electron’s orbital within an atom. It helps in understanding the electronic structure and behavior of atoms, as well as the properties and behavior of chemical bonds.
Magnetic Quantum Number
The magnetic quantum number, denoted as ml, is one of the four quantum numbers used to describe an electron in an atom. It specifies the orientation or direction of the orbital in which the electron is present. The value of ml can range from -l to +l, where l is the orbital quantum number.
The magnetic quantum number determines the number of possible orbitals within a given subshell. Each orbital within a subshell has a unique ml value, which describes its spatial orientation in relation to the external magnetic field. For example, in the p subshell, which has l = 1, there are three possible orbitals with ml values of -1, 0, and +1.
The magnetic quantum number also affects the energy levels of electrons. Electrons with different ml values have different energies, even if they are in the same subshell. This is due to the different spatial orientations and interactions with the magnetic field. The energy levels of electrons within an atom are determined by the combination of all four quantum numbers.
In summary, the magnetic quantum number determines the orientation of an electron’s orbital within an atom and affects the number of possible orbitals within a subshell. It is an important factor in determining the properties and behavior of electrons in atoms.
Spin Quantum Number
The spin quantum number is an important concept in quantum mechanics that describes the intrinsic angular momentum of a particle. It is denoted by the symbol “s” and can have two possible values: +1/2 and -1/2. This quantum number is related to the observable phenomenon known as spin, which is a property of elementary particles like electrons and protons.
The spin quantum number is often visualized as the rotation of a particle around its axis. However, it is important to note that this visualization is only an analogy, as spin is not related to physical rotation in the classical sense. Instead, the spin of a particle is a fundamental property that cannot be directly measured. It can only be inferred through its effects on other observable quantities.
In addition to its role in describing the intrinsic angular momentum of particles, the spin quantum number also affects other quantum mechanical properties. For example, it determines the behavior of particles in the presence of magnetic fields. The spin of a particle can align or anti-align with the direction of a magnetic field, leading to different energy levels and magnetic properties.
Furthermore, the spin quantum number is used in the classification of particles and their interactions. It is an essential component of the quantum mechanical description of particles, helping to explain phenomena such as the Pauli exclusion principle and the structure of atoms and molecules.
In summary, the spin quantum number is a fundamental concept in quantum mechanics that describes the intrinsic angular momentum of particles. It influences various properties and behaviors of particles, making it a crucial aspect of the quantum mechanical understanding of the microscopic world.
Practice Problems with Quantum Numbers
In quantum mechanics, quantum numbers are used to describe the properties of particles and their states. These numbers provide information about various aspects of an electron, such as its energy, spin, and orbital shape. Understanding how to interpret and use quantum numbers is essential for solving problems in quantum mechanics.
Here are some practice problems to help you further your understanding of quantum numbers:
Problem 1:
Consider an electron in the second energy level (n=2) of an atom. Determine the possible values of the azimuthal quantum number (l) for this electron.
Problem 2:
An electron has a spin quantum number (s) of +1/2. Determine the possible values of the magnetic quantum number (ml) for this electron.
Problem 3:
An electron occupies a p orbital. Determine the possible values of the principal quantum number (n), azimuthal quantum number (l), and magnetic quantum number (ml) for this electron.
Problem 4:
Consider an atom with an electron in the ground state. Determine the possible values of the principal quantum number (n), azimuthal quantum number (l), and magnetic quantum number (ml) for this electron.
Hint: Remember that the principal quantum number (n) can take on any positive integer value, the azimuthal quantum number (l) can range from 0 to (n-1), and the magnetic quantum number (ml) can range from -l to +l.
By solving these practice problems and understanding the rules and restrictions associated with quantum numbers, you will be better equipped to tackle more complex problems in quantum mechanics.
Quantum Numbers Practice Problems with Answers PDF
In the study of quantum mechanics, quantum numbers play a crucial role in describing the characteristics of atomic and subatomic particles. These numbers help define the energy levels and spatial distribution of electrons within an atom. To gain a better understanding of quantum numbers, it is important to practice solving problems that involve their application.
A useful resource for practicing quantum number problems is the Quantum Numbers Practice Problems with Answers PDF. This PDF document contains a variety of problems that cover different aspects of quantum numbers, including principal quantum number, azimuthal quantum number, magnetic quantum number, and spin quantum number. By solving these problems, students can improve their understanding of how quantum numbers determine the properties and behaviors of particles.
The Quantum Numbers Practice Problems with Answers PDF provides clear explanations and step-by-step solutions to each problem, making it a valuable tool for self-study or as a supplement to classroom instruction. The document also includes answer keys, allowing students to check their work and assess their progress. It covers topics such as electron configuration, orbital shape and orientation, and electron spin. By working through these problems, students can develop their problem-solving skills and gain confidence in their ability to apply quantum numbers to real-world scenarios.
Overall, the Quantum Numbers Practice Problems with Answers PDF is a valuable resource for anyone studying quantum mechanics or preparing for exams. It offers a comprehensive set of problems and solutions that enable students to deepen their understanding of quantum numbers and their significance in atomic and subatomic systems. Whether used as a study aid or for additional practice, this PDF document is an essential tool for mastering the concept of quantum numbers.
Key phrases:
- Quantum mechanics
- Quantum numbers
- Energy levels
- Spatial distribution
- Electrons
- Principal quantum number
- Azimuthal quantum number
- Magnetic quantum number
- Spin quantum number
- Solving problems
- Step-by-step solutions
- Electron configuration
- Orbital shape
- Electron spin
- Problem-solving skills
- Real-world scenarios
- Exam preparation