
In statistics, scatter plots and lines of best fit are useful tools for visualizing and analyzing data. A scatter plot is a graph that displays the relationship between two variables by plotting individual data points. The x-axis represents one variable and the y-axis represents the other variable. The data points are then plotted on the graph, creating a pattern or trend.
Lines of best fit, also known as trend lines or regression lines, are used to summarize the relationship between the two variables. These lines are drawn through the data points in the scatter plot to show the general direction of the relationship. The goal of a line of best fit is to minimize the distance between the data points and the line, providing a summary of the overall trend.
When working with scatter plots and lines of best fit, it is important to understand how to interpret the graph and the information it provides. The slope of the line of best fit can indicate the direction and strength of the relationship between the variables. A positive slope indicates a positive relationship, where an increase in one variable is associated with an increase in the other variable. A negative slope indicates a negative relationship, where an increase in one variable is associated with a decrease in the other variable.
Understanding scatter plots and lines of best fit
A scatter plot is a graphical representation of data points that show the relationship between two variables. It is used to determine if there is a correlation between the variables and if there is a linear or nonlinear relationship. The scatter plot consists of points, each representing an observation, plotted on a horizontal axis (x-axis) and a vertical axis (y-axis).
The line of best fit is a straight line that represents the average relationship between the variables in the scatter plot. It is used to make predictions or estimate values based on the data. The line of best fit is determined by minimizing the sum of the squares of the distances between the observed data points and the line.
Key phrases:
- Scatter plot
- Graphical representation
- Relationship between variables
- Correlation
- Linear or nonlinear
- Data points
- Horizontal axis (x-axis)
- Vertical axis (y-axis)
- Line of best fit
- Straight line
- Average relationship
- Predictions
- Estimate values
- Minimizing sum of squares
- Observed data points
The scatter plot and line of best fit are important tools in data analysis and can provide valuable insights into the relationship between variables. By analyzing the scatter plot and observing the trend of the data points, we can make predictions or draw conclusions about how changes in one variable may impact the other. The line of best fit helps to summarize the overall pattern in the data and allows us to estimate values for different variables.
Understanding scatter plots and lines of best fit is crucial in various fields such as statistics, economics, and social sciences. They help researchers and analysts to interpret data, identify trends, and make informed decisions. By visualizing the data through scatter plots and fitting a line of best fit, we can gain a better understanding of the underlying patterns and relationships in the data.
Overview of the Worksheet
The “Scatter plots and lines of best fit” worksheet is designed to help students practice interpreting scatter plots and calculating lines of best fit. The worksheet includes a series of questions and exercises that require students to analyze data and create scatter plots.
The worksheet begins with an introduction to scatter plots and their use in representing data. It explains how scatter plots are created by plotting pairs of data points on a coordinate plane. The worksheet then provides examples of scatter plots and asks students to identify the directional relationship between the variables.
After the introduction, the worksheet moves on to the concept of a line of best fit. It explains that a line of best fit is a straight line that represents the general trend of the data. The worksheet includes step-by-step instructions on how to calculate a line of best fit using the least squares regression method.
The remainder of the worksheet includes exercises and questions that require students to apply their knowledge of scatter plots and lines of best fit. These exercises involve interpreting scatter plots, calculating lines of best fit, and making predictions based on the data. Some questions also ask students to compare different scatter plots and analyze the strengths and weaknesses of different lines of best fit.
In conclusion, the “Scatter plots and lines of best fit” worksheet provides students with a comprehensive overview of scatter plots and the concept of lines of best fit. It helps students develop their skills in interpreting data, creating scatter plots, and calculating lines of best fit. By practicing these skills, students will gain a deeper understanding of how to analyze and interpret data using scatter plots.
The Importance of Finding the Answer Key
When it comes to educational materials such as worksheets and assignments, finding the answer key can be an essential resource for both students and teachers alike. The answer key provides a solution or a model answer to the problems or questions presented, allowing students to check their work and assess their understanding of the material. It serves as a valuable tool for self-assessment and identifying areas that may require further study or clarification.
For students, having access to the answer key can help enhance their learning experience. By comparing their answers to the correct ones, students can identify any mistakes they may have made and learn from them. They can also gain a better understanding of the reasoning and techniques required to arrive at the correct solutions. This feedback loop allows students to actively engage with the material, reinforce their learning, and build their confidence in problem-solving.
Moreover, the answer key can also be beneficial for teachers in various ways. It serves as a guide for grading students’ work, ensuring consistency and fairness in the evaluation process. With the answer key, teachers can quickly identify common misconceptions or patterns of errors among students, allowing them to address these areas during class discussions or follow-up activities. Additionally, it can save teachers time in preparing instructional materials by providing ready-made solutions that can be used as examples or models for teaching.
The availability of answer keys promotes independent learning and critical thinking. Students can use the answer key as a resource to compare their approach to problem-solving with the suggested solutions. This process encourages students to think deeply about their strategies and consider alternative approaches. It fosters a sense of empowerment and autonomy in students, as they actively participate in the learning process and take ownership of their academic progress.
In conclusion, the answer key plays a vital role in education. It not only helps students gauge their understanding of the material but also provides valuable feedback for improvement. For teachers, the answer key facilitates the grading process and serves as a valuable teaching resource. Thus, finding the answer key is crucial for an effective learning experience.
Step-by-step instructions for completing the worksheet
In order to successfully complete the Scatter Plots and Lines of Best Fit worksheet, follow these step-by-step instructions:
- Read the instructions: Begin by carefully reading the instructions provided on the worksheet. This will give you a clear understanding of the goals and objectives of the exercise.
- Gather the necessary materials: Collect all the materials you will need to complete the worksheet, including a pencil, ruler, and graphing paper.
- Create the scatter plot: Use the data provided on the worksheet to create a scatter plot on the graphing paper. Plot the points accurately, making sure to label the x-axis and y-axis appropriately.
- Determine the line of best fit: Analyze the scatter plot and identify the general trend or pattern. Determine the line of best fit that represents the relationship between the variables being studied.
- Calculate the equation of the line: Use the slope-intercept form (y = mx + b) to calculate the equation of the line of best fit. Determine the values of m (slope) and b (y-intercept) based on the data points and their relationship.
- Check your work: Review your scatter plot and line of best fit to ensure that they align with the given data and represent the relationship accurately. Double-check all calculations for accuracy.
- Answer the questions: Finally, answer the questions provided on the worksheet using the information gathered from the scatter plot and the line of best fit. Provide clear and concise explanations for your answers and support them with evidence from the graph.
By following these step-by-step instructions, you will be able to successfully complete the Scatter Plots and Lines of Best Fit worksheet and demonstrate your understanding of these important concepts in graphing and data analysis.
Common Misconceptions and Troubleshooting Tips
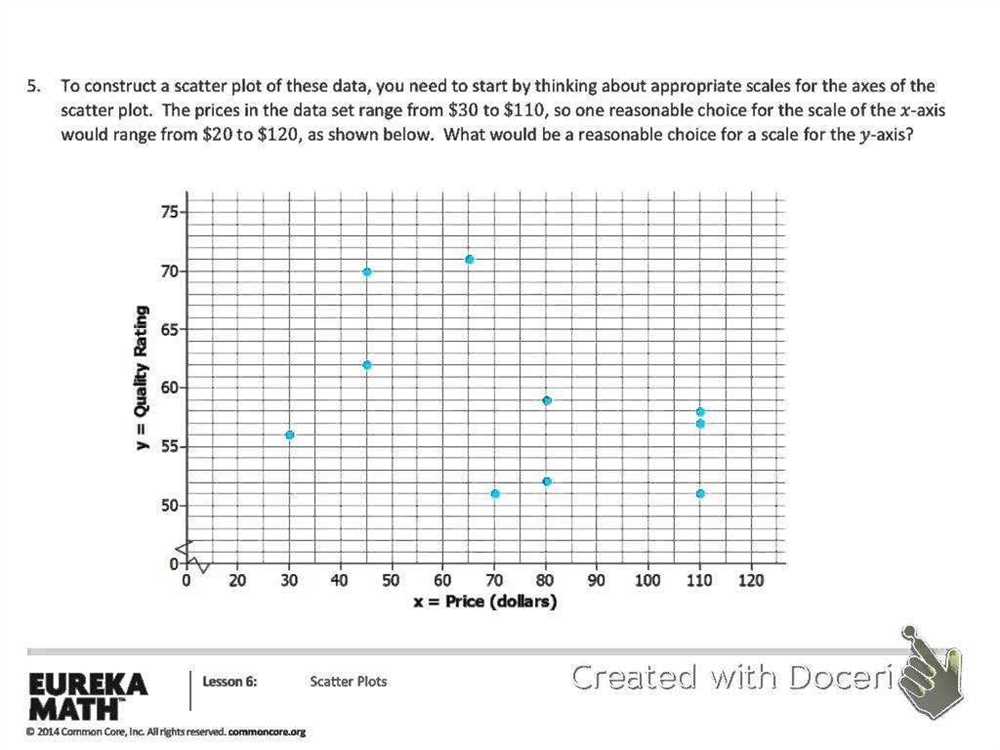
Scatter plots and lines of best fit can sometimes be challenging for students to understand and interpret. Here are some common misconceptions and troubleshooting tips to help clarify the concepts:
Misconception 1: The line of best fit must go through all the data points.
One common misconception is that the line of best fit should pass through every point on the scatter plot. However, this is not always the case. The line of best fit is an approximation of the overall trend in the data, and it may not perfectly align with each individual point. Encourage students to understand that the line of best fit represents the average relationship between the variables.
Misconception 2: The line of best fit determines causation.
Another misconception is that the line of best fit indicates a cause-and-effect relationship between the variables. It is important to emphasize that correlation does not imply causation. Just because two variables have a strong linear relationship does not mean that one variable causes the other. Remind students to be cautious when making causal claims based solely on the line of best fit.
Troubleshooting Tip 1: Outliers
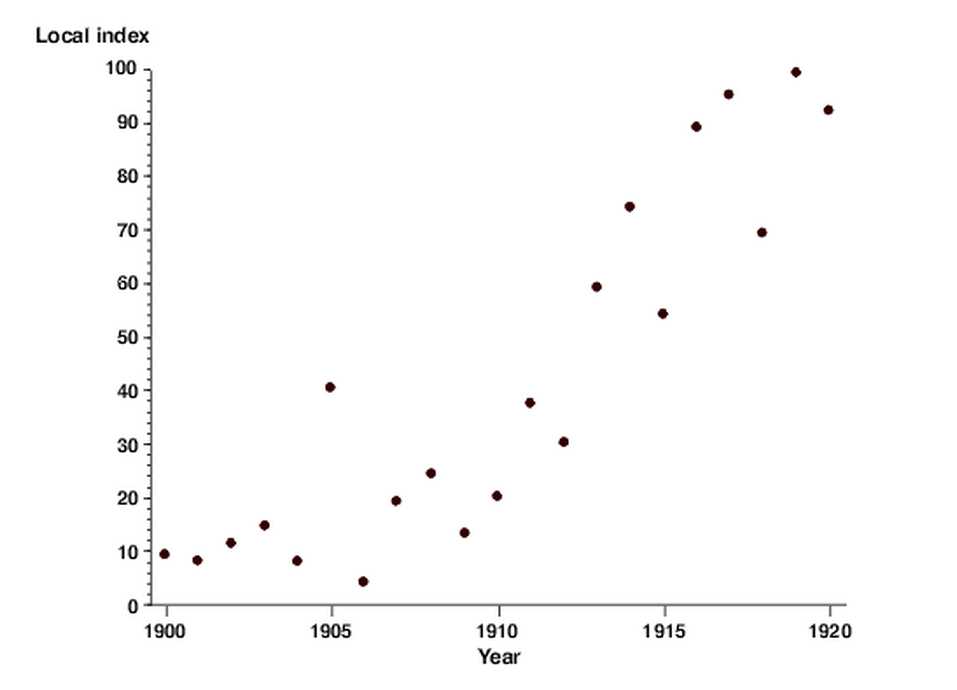
When analyzing scatter plots, outliers can greatly affect the line of best fit. If there are extreme data points that do not follow the general trend, they can pull the line away from the majority of the data. Encourage students to identify and analyze outliers separately from the rest of the data, as they can have a significant impact on the line of best fit.
Troubleshooting Tip 2: Non-linear Relationships
Scatter plots are commonly used to analyze linear relationships, but it’s important to recognize that not all relationships are linear. Sometimes, the data may follow a different pattern, such as exponential or quadratic. If the scatter plot does not have a clear linear trend, it may be necessary to explore other functions or transformations to better model the data.
By addressing these common misconceptions and providing students with troubleshooting tips, we can help them better understand scatter plots and lines of best fit and build their critical thinking skills in data analysis.
Analysing and Interpreting the Results
When analyzing scatter plots and lines of best fit, there are several key observations and interpretations that can be made.
Relation between variables: Firstly, it is important to look at the overall trend of the scatter plot to determine the relationship between the variables being plotted. If the points on the plot are clustered closely together and form a clear pattern, it suggests a strong correlation between the variables. On the other hand, if the points are scattered and do not appear to follow any specific trend, it indicates a weak or no correlation.
Line of best fit: The line of best fit is a visual representation of the relationship between the variables in the scatter plot. It can be used to estimate the value of one variable based on the value of another variable. When examining the line of best fit, it is important to consider its slope and y-intercept. The slope indicates the rate of change between the variables, while the y-intercept represents the starting point of the line. A steeper slope suggests a stronger correlation, while a y-intercept away from zero indicates a bias in the data.
Outliers: Another important aspect of analyzing scatter plots is identifying any outliers. Outliers are data points that significantly deviate from the overall pattern or trend of the scatter plot. These points can have a major impact on the line of best fit and can potentially skew the interpretation of the results. It is important to investigate and understand the reasons for any outliers and decide if they should be included or excluded in the analysis.
Strength of correlation: Lastly, it is valuable to assess the strength of the correlation between the variables. This can be done by calculating the correlation coefficient, which measures the strength and direction of the relationship between two variables. A coefficient of +1 or -1 indicates a strong positive or negative correlation, while a coefficient close to 0 suggests no correlation. This information can provide insight into the level of predictability or association between the variables being studied.
In conclusion, analyzing and interpreting the results of scatter plots and lines of best fit involves considering the overall trend of the plot, the line of best fit, the presence of outliers, and the strength of the correlation. These observations and interpretations can help draw meaningful conclusions and make predictions about the relationship between the variables being studied.
Tips for further practice and improvement
Scatter plots and lines of best fit can be a challenging concept to grasp, but with practice and dedication, you can improve your understanding and skills. Here are some tips to help you further practice and improve:
- Review the basic concepts: Before diving into complex scatter plots and lines of best fit, make sure you have a solid understanding of the basic concepts. Familiarize yourself with the terms, such as dependent variable, independent variable, and correlation.
- Practice with real-world examples: Look for real-world examples that involve scatter plots and lines of best fit. By working with actual data, you can gain a better understanding of how to interpret and analyze scatter plots in different contexts.
- Create your own scatter plots: Take the initiative to create your own scatter plots using different sets of data. This will allow you to practice plotting points accurately and understanding the relationship between variables.
- Explore different line fitting techniques: While the line of best fit is the most commonly used technique, there are other methods to fit lines to scatter plots, such as polynomial regression. Experiment with these techniques to gain a more comprehensive understanding.
- Seek additional resources: If you’re struggling to grasp certain concepts or techniques, don’t hesitate to seek additional resources such as textbooks, online tutorials, or even consult with a teacher or tutor. Different perspectives and explanations can often help solidify your understanding.
- Challenge yourself with complex problems: As you become more comfortable with scatter plots and lines of best fit, challenge yourself with more complex problems. This will help you develop problem-solving skills and apply your knowledge to different scenarios.
Remember, practice is key when it comes to mastering scatter plots and lines of best fit. By implementing these tips and dedicating time to review and practice regularly, you’ll be well on your way to improving your skills and understanding of this topic.