
Secondary Math 1 Module 1 Sequences 1-3 introduces students to the foundational concepts of sequences in mathematics. By understanding the key principles and techniques used to solve problems related to sequences, students gain a solid foundation for more advanced mathematical topics.
This answer key serves as a valuable resource for both students and educators alike. It offers a comprehensive breakdown of the solutions to the exercises provided in Sequences 1-3, allowing students to check their work and better understand the steps involved in arriving at the correct answers.
Through the use of clear explanations and step-by-step solutions, this answer key helps students develop their problem-solving skills and enhance their understanding of the underlying concepts. It provides a valuable tool for students to assess their progress and reinforce their learning.
Secondary Math 1 Module 1 Sequences 1-3 Answer Key
In Secondary Math 1 Module 1, students explore the concept of sequences, which are ordered lists of numbers or objects. In sequences 1-3, students learn about arithmetic sequences, geometric sequences, and explicit formulas for finding the nth term of a sequence.
An arithmetic sequence is a sequence in which the difference between consecutive terms is constant. To find the next term in an arithmetic sequence, you add or subtract the same value from the previous term. The explicit formula for finding the nth term of an arithmetic sequence is: an = a1 + (n – 1)d, where an is the nth term, a1 is the first term, n is the position of the term, and d is the common difference.
A geometric sequence is a sequence in which the ratio between consecutive terms is constant. To find the next term in a geometric sequence, you multiply or divide the previous term by the same value. The explicit formula for finding the nth term of a geometric sequence is: an = a1 * r(n – 1), where an is the nth term, a1 is the first term, n is the position of the term, and r is the common ratio.
In the answer key for sequences 1-3, you will find the explicit formulas for arithmetic and geometric sequences, as well as step-by-step solutions for finding the nth term of a given sequence. This answer key will help you check your work and understand the process of finding the nth term in different types of sequences.
Example:
Let’s say you are given an arithmetic sequence with a first term of 2 and a common difference of 3. You need to find the 8th term of the sequence. Using the explicit formula for arithmetic sequences, you can plug in the values into the formula:
a8 = 2 + (8 – 1) * 3
a8 = 2 + 7 * 3
a8 = 2 + 21
a8 = 23
- The 8th term of the arithmetic sequence is 23.
The answer key for sequences 1-3 will provide similar step-by-step solutions for different types of sequences, helping you understand the concepts better and improve your problem-solving skills in Secondary Math 1.
Overview of Secondary Math 1 Module 1 Sequences 1-3
The Secondary Math 1 Module 1 Sequences 1-3 is a comprehensive curriculum that focuses on the study of different types of sequences. The module is designed to provide students with a deep understanding of arithmetic and geometric sequences, as well as recursive and explicit formulas.
Throughout the module, students will explore the concept of a sequence, which is a list of numbers arranged in a specific order. They will learn how to identify the common difference in an arithmetic sequence and the common ratio in a geometric sequence. By understanding these key concepts, students will be able to accurately generate the terms of a given sequence and predict future terms.
The module is divided into three sections, each covering a specific type of sequence. In Sequences 1, students will focus on arithmetic sequences and learn how to identify the common difference using a given formula or a set of terms. They will also practice finding missing terms in arithmetic sequences and identify the nth term of a sequence.
In Sequences 2, students will shift their focus to geometric sequences. They will learn how to identify the common ratio using a given formula or a set of terms. Like with arithmetic sequences, they will practice finding missing terms and identifying the nth term of a geometric sequence.
Finally, in Sequences 3, students will explore both recursive and explicit formulas. They will learn how to generate terms of a sequence using a recursive formula and vice versa. They will also practice finding explicit formulas for arithmetic and geometric sequences.
By the end of Secondary Math 1 Module 1 Sequences 1-3, students will have a solid understanding of various types of sequences and the tools to analyze and generate terms in a sequence. This foundation will be essential as they progress further into the study of higher-level mathematics.
Understanding Sequences in Secondary Math 1
In Secondary Math 1, students begin to explore the concept of sequences, which are ordered lists of numbers or objects. Understanding and analyzing sequences is an important skill in mathematics as it can help students identify patterns, make predictions, and solve problems more effectively.
Sequences can be categorized into different types, such as arithmetic sequences, geometric sequences, and recursive sequences. Arithmetic sequences involve adding a constant difference between each consecutive term, while geometric sequences involve multiplying by a constant ratio. Recursive sequences, on the other hand, rely on a specific formula or function to generate each term based on the previous terms.
One key aspect of understanding sequences is being able to identify the explicit formula or pattern that governs the sequence. This formula can be used to find any term in the sequence without having to calculate each term individually. Students learn to use algebraic expressions and equations to represent and solve for the terms in a sequence.
Sequences are used in various contexts in secondary math, such as in modeling real-life scenarios, analyzing mathematical patterns, and solving problems involving summation and series. By understanding sequences, students develop critical thinking skills, logical reasoning, and the ability to generalize patterns and relationships.
Key Concepts and Formulas in Secondary Math 1 Module 1 Sequences 1-3

In Secondary Math 1 Module 1 Sequences 1-3, students learn about key concepts and formulas related to sequences. A sequence is an ordered list of numbers with a specific pattern. Understanding the concepts and formulas will help students analyze and solve problems involving sequences.
One key concept in this module is arithmetic sequences. An arithmetic sequence is a sequence in which the difference between consecutive terms is constant. The formula to find the nth term of an arithmetic sequence is: an = a1 + (n – 1)d, where an is the nth term, a1 is the first term, n is the position of the term, and d is the common difference.
Another key concept is geometric sequences. A geometric sequence is a sequence in which the ratio between consecutive terms is constant. The formula to find the nth term of a geometric sequence is: an = a1 * r(n – 1), where an is the nth term, a1 is the first term, r is the common ratio, and n is the position of the term.
Other topics covered in this module include sums of arithmetic sequences, sums of geometric sequences, and identifying both arithmetic and geometric sequences in real-life contexts. By mastering these key concepts and formulas, students will be equipped to solve various types of sequence problems and apply their knowledge to real-world situations.
Practice Problems for Secondary Math 1 Module 1 Sequences 1-3
In Secondary Math 1 Module 1, students learn about sequences and their properties. Sequences are ordered lists of numbers that follow a pattern or rule. This module introduces students to arithmetic and geometric sequences, as well as their recursive and explicit formulas.
To master the concepts taught in Module 1, it is important for students to practice solving problems and applying the formulas for arithmetic and geometric sequences. Here are some practice problems to help reinforce the material:
Arithmetic Sequences Practice:
- Find the common difference of the arithmetic sequence: 2, 5, 8, 11, 14, …
- Write the explicit formula for the arithmetic sequence: 3, 8, 13, 18, 23, …
- Determine the 53rd term of the arithmetic sequence: 7, 11, 15, 19, …
Geometric Sequences Practice:
- Find the common ratio of the geometric sequence: 3, 6, 12, 24, …
- Write the recursive formula for the geometric sequence: 2, 10, 50, 250, …
- Determine the sum of the first 10 terms of the geometric sequence: 4, 8, 16, 32, …
By practicing these types of problems, students will become more proficient in identifying arithmetic and geometric sequences, finding their common differences or ratios, and using the appropriate formulas to find specific terms or sums. This will lay a solid foundation for further mathematical studies in secondary math and beyond.
Steps for Finding the Answer Key for Secondary Math 1 Module 1 Sequences 1-3
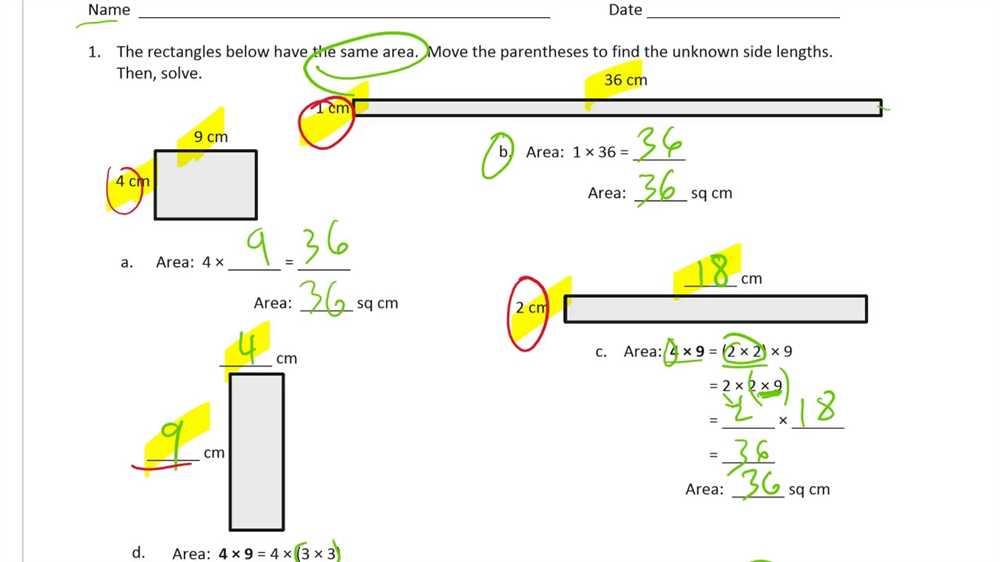
Secondary Math 1 Module 1 focuses on sequences and their properties. Finding the answer key for this module can be a helpful tool for students to check their work and ensure understanding. Below are the steps to find the answer key for Secondary Math 1 Module 1 Sequences 1-3.
Step 1: Start with the Textbook

The first place to look for the answer key is in the textbook. Most textbooks include an answer key section at the end of the book. Check the index or table of contents to find the specific section for sequences and locate the corresponding answer key pages.
Step 2: Check the Online Resources
If the answer key is not available in the textbook, check the publisher’s website or any online resources provided by the school or district. Many publishers offer online support materials for their textbooks, including answer keys. Look for a section or resource specifically for Secondary Math 1 Module 1 Sequences 1-3.
Step 3: Ask the Teacher
If the answer key is still not found, reach out to the teacher for assistance. The teacher may have access to additional resources or be able to provide guidance on where to find the answer key. They can also clarify any specific instructions or expectations regarding the use of answer keys.
By following these steps, students can find the answer key for Secondary Math 1 Module 1 Sequences 1-3 and utilize it as a valuable tool for learning and self-assessment in their math studies.
Tips and Tricks for Solving Sequences in Secondary Math 1
Sequences are an important topic in Secondary Math 1, and understanding how to solve them is crucial for success in the subject. Here are some tips and tricks that can help you tackle sequence problems with confidence:
1. Recognize the pattern:
When given a sequence, the first step is to identify any patterns or relationships between the terms. Look for recurring differences, common ratios, or any other consistent characteristics that can help you determine the formula for the sequence.
2. Use the formula:
Once you have identified the pattern, use it to create a formula that relates the nth term to the previous terms. This formula will allow you to find any term in the sequence, given its position.
3. Determine the missing term:
If you are given a sequence with one or more missing terms, use the formula to determine the value of the missing term. Plug in the known values and solve for the unknown.
4. Watch out for common sequence types:
Sequences can come in various forms, such as arithmetic, geometric, or even Fibonacci. Familiarize yourself with the characteristics and formulas for each type, as they can provide valuable clues for solving the sequence.
5. Check your answer:
After finding the solution, always double-check your work by plugging the value back into the formula and confirming that it matches the other terms in the sequence.
By following these tips and tricks, you’ll be well-equipped to tackle sequence problems in Secondary Math 1 with confidence and accuracy.
Common Mistakes to Avoid in Secondary Math 1 Module 1 Sequences 1-3
When studying sequences in Secondary Math 1 Module 1, it is important to pay attention to common mistakes that students often make. By being aware of these mistakes, you can avoid them and improve your understanding of the material.
1. Misunderstanding the Notation:
One common mistake is misunderstanding the notation used in sequences. It is important to carefully read and interpret the given information. Pay attention to the terms and their corresponding values. Remember that a sequence is an ordered list of numbers that follow a certain pattern.
2. Incorrectly Identifying the Type of Sequence:
Another mistake is incorrectly identifying the type of sequence. Sequences can be arithmetic, geometric, or neither. It is crucial to properly analyze the given terms and find the pattern. For arithmetic sequences, the difference between consecutive terms is constant. For geometric sequences, the ratio between consecutive terms is constant. Take your time to identify the correct type of sequence.
3. Skipping Steps in Calculations:
Skipping steps in calculations is a common mistake that can lead to incorrect answers. It is important to show all the steps and calculations involved in solving a problem. Pay attention to details and double-check your work. This will help you catch any errors and improve your accuracy in solving sequence problems.
4. Failing to Check for Extraneous Solutions:
When solving equations involving sequences, it is crucial to check for extraneous solutions. Sometimes, a solution may satisfy the equation algebraically but may not make sense in the context of the sequence. Always substitute the found solution back into the original equation to ensure it is valid.
By being aware of these common mistakes, you can avoid them and strengthen your understanding of sequences in Secondary Math 1 Module 1. Remember to carefully interpret notation, correctly identify the type of sequence, show all steps in calculations, and check for extraneous solutions. With practice and attention to detail, you will improve your skills in solving sequence problems.