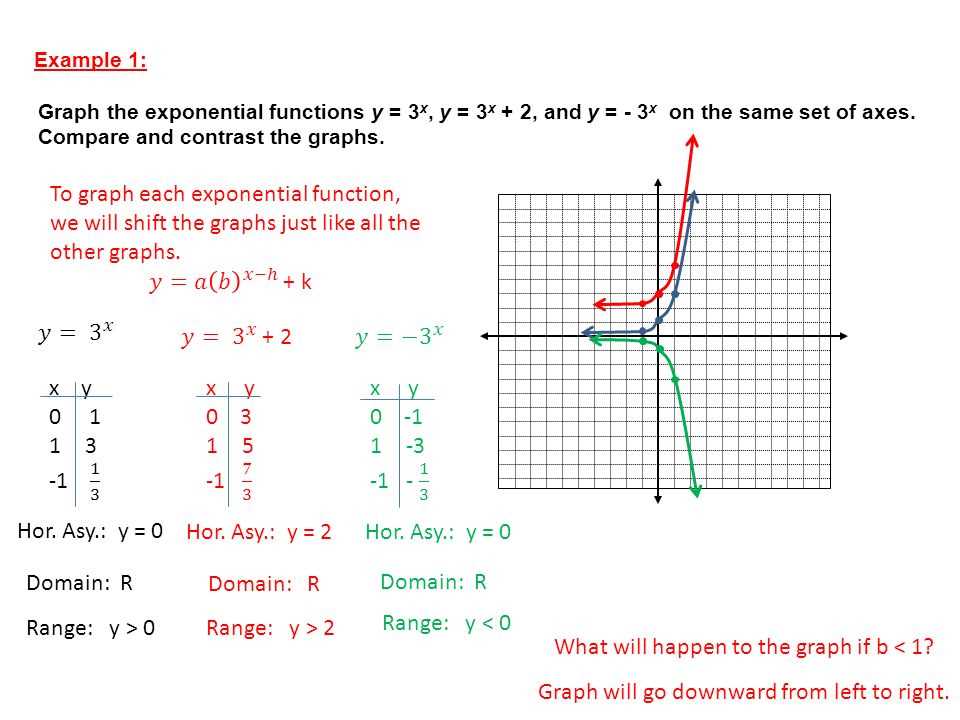
The study of exponential functions and their graphs is crucial in understanding various real-world phenomena. In Section 7.1 and 7.2 of our mathematics course, we delve deeper into the properties and characteristics of exponential graphs. By analyzing the answer key provided, students can gain a comprehensive understanding of these graphs and their key features.
Exponential graphs represent a wide range of natural phenomena, such as population growth, radioactive decay, and compound interest. The shape of these graphs differs from that of linear or quadratic functions, as they exhibit exponential growth or decay. Understanding the key features of exponential graphs, such as the asymptote, y-intercept, and rate of growth or decay, is essential for interpreting and analyzing real-world data.
In Section 7.1, we focus on exponential growth. By examining the answer key, students can learn how to identify the rate of growth and interpret the graph’s behavior. They will discover that exponential functions with positive growth rates gradually increase over time, becoming steeper as the rate of growth increases. They will also gain insights into how factors such as the initial value and the rate of growth affect the shape and behavior of the graph.
In Section 7.2, we shift our attention to exponential decay. Through the answer key, students will learn how to recognize exponential decay in a graph and differentiate it from exponential growth. They will observe that exponential decay functions exhibit a gradual decrease over time, approaching an asymptote. By analyzing the rate of decay and the initial value, students can gain a deeper understanding of the behavior of exponential decay graphs.
Understanding Exponential Graphs: What is Section 7 1 and 7 2?

The study of exponential graphs is an important part of mathematics and is covered in Section 7 1 and 7 2 of most math curriculums. These sections explore the properties and behavior of exponential functions, which are functions that grow or decay at a constant rate.
In Section 7 1, students learn about the basic form of an exponential function, which is given by the equation f(x) = ab^x, where a is a constant base and b is the growth or decay factor. This section introduces students to the key features of exponential graphs, such as the shape of the graph, the domain and range, and the x and y intercepts. It also teaches students how to identify the growth or decay factor and how to write an exponential equation given certain information about the graph.
In Section 7 2, students dive deeper into the properties of exponential graphs. They learn how to create exponential models to represent real-world situations and use these models to make predictions and solve problems. This section also covers transformations of exponential graphs, such as vertical and horizontal shifts, reflections, and stretches. Students will learn how these transformations affect the graph and how to write the equation of a transformed exponential graph.
In order to fully understand exponential graphs and their applications, it is essential to master the concepts covered in Section 7 1 and 7 2. These sections provide the foundation for further exploration of exponential functions and their relevance in fields such as economics, science, and engineering. By studying and practicing these concepts, students will develop the skills necessary to analyze and interpret exponential graphs, and apply their knowledge to solve real-world problems.
The Definition of an Exponential Function
An exponential function is a mathematical expression that represents the relationship between a base number and its exponent. It can be written in the form of y = ab^x, where y is the dependent variable, a is a constant multiplier called the initial value or starting value, b is the base, and x is the independent variable.
The base of an exponential function determines the rate at which the function grows or decays. If b is greater than 1, the function is an exponential growth function, and as x increases, y increases at an increasing rate. On the other hand, if b is between 0 and 1, the function is an exponential decay function, and as x increases, y decreases at a decreasing rate.
Exponential functions can be used to model various real-life phenomena, such as population growth, compound interest, radioactive decay, and bacterial growth. They are commonly used in fields such as economics, biology, finance, and physics to analyze data and make predictions.
When graphed, exponential functions exhibit specific characteristics. The graph of an exponential growth function starts at the y-intercept and curves upward as x increases. The graph of an exponential decay function starts at the y-intercept and curves downward as x increases. The rate of growth or decay is determined by the base.
In summary, exponential functions describe the relationship between a base number and its exponent. They can be used to model various real-life phenomena and exhibit distinct characteristics when graphed. Understanding the basics of exponential functions is essential for solving problems and analyzing data in many disciplines.
The General Form of an Exponential Function
An exponential function is a mathematical function in the form of y = a * b^x, where a and b are constants and x is the independent variable. This form represents the general equation for exponential growth or decay.
The constant a represents the initial value of the function, or the value of y when x is equal to 0. It is the y-intercept of the graph of the function. The constant b represents the base of the exponential function, which is typically greater than 1 for exponential growth or between 0 and 1 for exponential decay.
The graph of an exponential function has certain characteristics. When b is greater than 1, the graph rises from left to right, indicating exponential growth. When b is between 0 and 1, the graph decreases from left to right, indicating exponential decay. The steepness of the curve depends on the value of b, with larger values of b resulting in steeper curves.
Exponential functions can be used to model various real-world phenomena, such as population growth, radioactive decay, and compound interest. By understanding the general form of an exponential function, we can analyze and interpret the behavior of these phenomena mathematically.
In conclusion, the general form of an exponential function is represented by the equation y = a * b^x, where a and b are constants. This form allows us to describe and study exponential growth and decay in various contexts, providing valuable insights into natural and man-made processes.
Identifying the Key Components of an Exponential Graph
An exponential graph represents a mathematical function that exhibits exponential growth or decay. Understanding the key components of an exponential graph is essential for interpreting and analyzing its behavior. The main components to look for are the initial value, the rate of growth or decay, and the asymptote.
Initial Value: The initial value is the starting point of the graph, often represented by the point (0, y). It shows the value of the function at the beginning of the time period or input range. In an exponential growth graph, the initial value is typically positive, indicating the starting amount. In an exponential decay graph, the initial value is usually larger than the final value and represents the initial amount decreasing over time.
Rate of Growth or Decay: The rate of growth or decay determines the steepness or slope of the graph. It represents how fast the function is increasing or decreasing as the input variable increases. The rate of growth or decay is usually represented by the base of the exponential function. A base greater than 1 signifies exponential growth, while a base between 0 and 1 represents exponential decay. The higher the base, the steeper the graph, and the faster the growth or decay.
Asymptote: The asymptote of an exponential graph is a horizontal line that the graph approaches but never intersects. It can be either above or below the x-axis, depending on whether the graph represents exponential growth or decay. The asymptote represents a limit or boundary that the function cannot surpass. It helps visualize the long-term behavior of the exponential function and can be used to calculate limits and evaluate the potential values of the graph.
By examining and understanding these key components, we can gain insights into the behavior and properties of exponential graphs. This knowledge allows us to make predictions, analyze trends, and solve real-world problems involving exponential functions.
Section 7 1: Graphing Exponential Functions with a Base of e
Exponential functions with a base of e, also known as natural exponential functions, have a special significance in mathematics and various scientific fields. The constant e is approximately equal to 2.71828 and is an irrational number that arises naturally in many mathematical and scientific contexts.
When graphing exponential functions with a base of e, we observe certain characteristics. Firstly, the graph of these functions always has a positive y-intercept at (0, 1), which means that the function value is 1 when the input is 0. This is true for any exponential function with a positive base. Additionally, the graph of an exponential function with a base of e is always increasing, as e is a positive number greater than 1.
Furthermore, the rate at which the function increases depends on the value of the input. As the base e is greater than 1, the function grows at an increasing rate as the input increases. This can be observed by comparing the slopes of the tangent lines at different points on the graph. The slope of a tangent line at any point on the graph represents the instantaneous rate of change, and for exponential functions with a base of e, this rate increases as the input value increases.
In general, graphing exponential functions with a base of e follows the same principles as graphing any exponential function. However, the special properties of the constant e make these functions particularly important and prevalent in various areas of mathematics and science. Understanding the characteristics and behavior of these functions is essential for analyzing exponential growth and decay phenomena that occur in nature, finance, biology, and other fields.
Reviewing the Properties of the Natural Exponential Function
The natural exponential function is a fundamental function in mathematics, commonly denoted as f(x) = e^x, where e is Euler’s number, approximately equal to 2.71828. The exponential function has several key properties that make it unique and useful in various mathematical and scientific applications.
One of the primary properties of the natural exponential function is its rapid growth rate. As the input variable x increases, the function grows at an increasingly faster pace. In other words, the function exhibits exponential growth. This property is particularly important in fields such as finance, biology, and population studies, where exponential growth occurs frequently.
Another essential property of the natural exponential function is its symmetry with respect to the y-axis. This means that for any value of x, the function’s value at -x is the reciprocal of its value at x. For example, f(-x) = 1/f(x). This symmetry is a fundamental property of exponential functions and can be observed in many real-world phenomena.
The natural exponential function also has the remarkable property of being its derivative. In other words, if we take the derivative of the function f(x) = e^x, we obtain the same function, f'(x) = e^x. This property is unique to the exponential function and is one of the reasons for its wide application in calculus and related fields.
In summary, the natural exponential function is a powerful mathematical tool with distinct properties that set it apart from other functions. Its rapid growth rate, symmetry, and the fact that it is its own derivative make it an invaluable function in various scientific and mathematical disciplines. Understanding and applying the properties of the natural exponential function is essential for solving problems and modeling real-world phenomena accurately.
Analyzing the Graphs of Exponential Functions with a Base of e
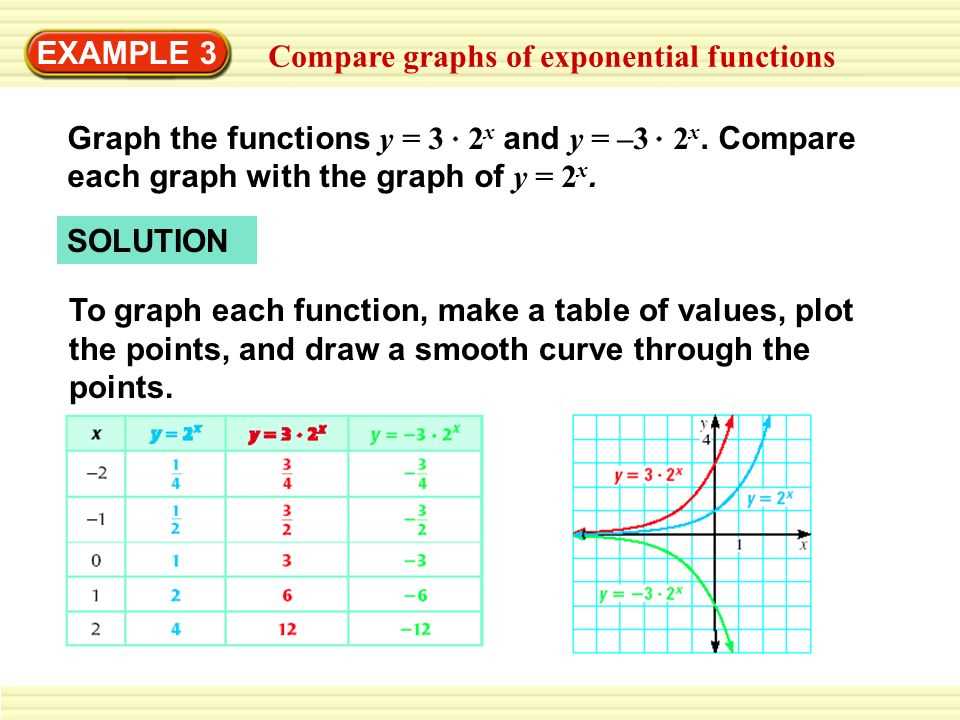
Exponential functions with a base of e, also known as natural exponential functions, have a unique set of properties and characteristics that can be analyzed through their graphs. The base e, approximately equal to 2.71828, is a mathematical constant that arises from the study of continuous compounding, and it has significant applications in various fields such as finance, physics, and biology.
When graphing exponential functions with a base of e, the general shape of the graph is a smooth, increasing curve that starts from the point (0, 1) and continues to grow infinitely. This is because the value of e raised to any power will always be positive and increasing as the exponent increases. The curve is always concave up, which means it curves upward as it moves from left to right.
The rate at which the function grows is determined by the coefficient in front of the exponential term. If the coefficient is positive, the graph will increase at an increasing rate as x moves to the right. If the coefficient is negative, the graph will decrease at a decreasing rate as x moves to the right, eventually approaching the x-axis but never crossing it.
The x-intercept of an exponential function with a base of e is at (0, 0), but the y-intercept does not exist since the graph starts from (0, 1). As x approaches negative infinity, the graph gets arbitrarily close to the x-axis but never touches it. As x approaches positive infinity, the graph grows rapidly, becoming steeper and steeper without bound.
It is also worth noting that the slope of the tangent line to the graph of an exponential function with a base of e at any point is equal to the y-coordinate of that point. This property is a consequence of the exponential function’s unique rate of growth and is useful in applications such as determining the instantaneous growth rate or decay rate at a specific point.
Overall, analyzing the graphs of exponential functions with a base of e provides valuable insights into their behavior and growth patterns. The continuous and increasing nature of these functions makes them important in various mathematical and real-world applications.