
Simple Harmonic Motion (SHM) is a fundamental concept in physics and engineering that describes the oscillatory motion of a system under the influence of a restoring force. Understanding the principles of SHM is essential for grasping various topics, such as waves, vibrations, and resonance.
For students and professionals seeking to enhance their understanding of SHM, multiple choice questions can be an effective tool for practice and assessment. These questions offer a structured approach to testing knowledge and identifying areas of improvement.
This article provides a collection of multiple choice questions and answers in PDF format for easy access and convenience. The questions cover various aspects of SHM, including equilibrium position, period, amplitude, and energy. They also address the relationships between different parameters and concepts related to SHM.
Definition and Examples
The concept of simple harmonic motion (SHM) refers to a type of oscillatory motion in which a system moves back and forth about a stable equilibrium position. It is characterized by a restoring force that is proportional to the displacement from the equilibrium position, and the motion follows a sinusoidal or sine wave pattern.
In simple harmonic motion, the restoring force acts in the opposite direction of the displacement from the equilibrium position, causing the system to oscillate back and forth. This restoring force arises from an underlying potential energy function, known as the potential energy of the system. The most common examples of simple harmonic motion include the motion of a mass-spring system and the motion of a pendulum.
In a mass-spring system, a mass is attached to a spring, and when the mass is displaced from its equilibrium position, the spring exerts a restoring force that brings the mass back to its equilibrium position. The motion of the mass is governed by Hooke’s law, which states that the force exerted by the spring is directly proportional to the displacement of the mass.
A pendulum is another example of simple harmonic motion, where a mass is attached to a string or rod and swings back and forth under the influence of gravity. The restoring force in this case is provided by the tension in the string or the rod, which brings the pendulum back to its equilibrium position.
- In a mass-spring system, the motion is governed by Hooke’s law and the restoring force is provided by the spring.
- In a pendulum, the restoring force is provided by the tension in the string or the rod.
These examples illustrate the principle of simple harmonic motion and its relation to restoring forces. Understanding and analyzing simple harmonic motion is essential in many branches of physics and engineering, as it provides insights into the behavior of oscillating systems and waves.
Equation of Motion
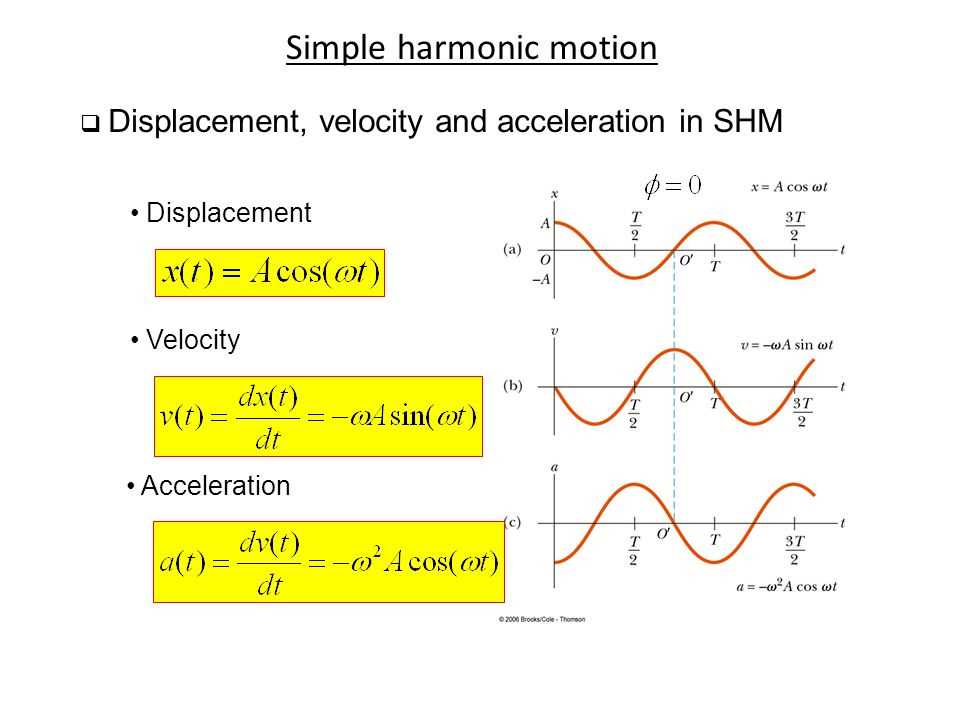
In simple harmonic motion (SHM), the equation of motion describes the relationship between the displacement (x) of an oscillating object and time (t). The equation of motion for an object undergoing SHM can be expressed as:
x(t) = A * cos(ωt + φ)
Where:
- x(t) is the displacement of the object at time t
- A is the amplitude of the motion, representing the maximum displacement of the object from its equilibrium position
- ω is the angular frequency, which determines the speed of oscillation
- t is the time
- φ is the phase constant, representing the initial phase of the motion
The equation of motion for SHM is derived from the physical principles governing the system and can be used to model and analyze the motion of objects undergoing harmonic oscillations. It provides a mathematical representation of how the displacement of an object changes with respect to time.
The equation of motion can be helpful in understanding various properties of an oscillating system, such as the periodicity of the motion, the amplitude, and the phase of the oscillation. By manipulating the equation of motion, one can derive relationships between different parameters and solve for unknown quantities in a given system. Furthermore, by graphing the equation of motion, one can visualize the behavior of the oscillating object over time.
Characteristics of Simple Harmonic Motion
In physics, simple harmonic motion (SHM) refers to the oscillatory motion of a system in which the force acting on the system is proportional to the displacement of the system from its equilibrium position. SHM is characterized by several key features.
Periodic Motion: Simple harmonic motion is a type of periodic motion, meaning the motion repeats itself over a specific time period. The system undergoes a complete cycle, or oscillation, and returns to its initial state after a certain amount of time known as the period.
Restoring Force: In SHM, there is always a restoring force that brings the system back to its equilibrium position. This restoring force is directly proportional to the displacement from the equilibrium position and acts in the opposite direction. It can be provided by a spring, the force of gravity, or other factors depending on the specific system.
Amplitude: The amplitude of SHM refers to the maximum displacement from the equilibrium position. It represents the maximum distance the system moves away from its mean position during an oscillation. The amplitude determines the extent of the motion and influences other characteristics such as the energy and frequency of the system.
Frequency: Frequency is a measure of how many oscillations occur per unit of time. In simple harmonic motion, the frequency is determined by the reciprocal of the period. It describes how quickly the system oscillates and is measured in hertz (Hz).
Phase: The phase of SHM describes the position of the system within one complete cycle. It is often represented by an angle and helps to determine the relationship between multiple oscillating systems. The phase can be used to calculate the displacement, velocity, and acceleration of the system at any given time.
Energy Conservation: In SHM, energy is conserved as the system oscillates back and forth. The potential energy of the system is highest at the extreme points of the motion, while the kinetic energy is highest at the equilibrium position. The total mechanical energy remains constant throughout the oscillation.
Overall, simple harmonic motion exhibits a predictable and repetitive pattern of motion due to the restoring force acting on the system. These characteristics make it a fundamental concept in physics and have applications in various fields including mechanics, acoustics, and electronics.
Amplitude, Period, and Frequency

In the context of simple harmonic motion, three important concepts to understand are amplitude, period, and frequency. These terms describe different aspects of the motion of an oscillating system.
Amplitude refers to the maximum displacement or distance from equilibrium that an oscillating object reaches. It represents the extent to which the object deviates from its equilibrium position. In other words, the amplitude measures the size or magnitude of the oscillation. It is usually denoted by the symbol A.
Period is the time it takes for one complete cycle of oscillation to occur. It is usually represented by the symbol T and is measured in seconds. The period of an oscillating system is determined by factors such as the mass and stiffness of the system. The period is inversely proportional to the frequency of the oscillation.
Frequency is the number of complete cycles or oscillations that occur in one second. It is measured in hertz (Hz) and is denoted by the symbol f. The frequency of an oscillating system is determined by factors such as the mass and stiffness of the system. It is directly proportional to the period of the oscillation.
The relationship between period and frequency can be expressed as:
- The period is equal to the reciprocal of the frequency: T = 1/f.
- The frequency is equal to the reciprocal of the period: f = 1/T.
Understanding the concepts of amplitude, period, and frequency is crucial in analyzing and predicting the behavior of systems undergoing simple harmonic motion.
Phase and Phase Constant

In simple harmonic motion, the phase refers to the position of an oscillating object at a particular point in time. It is represented by the angle, usually denoted by Φ, and is used to describe the relationship between the position, velocity, and acceleration of the object. The phase can be thought of as a measure of how far the object is into its oscillation cycle.
The phase constant, represented by Φ₀, is a constant that determines the starting position of the oscillating object. It is the angle at which the object is at t = 0, or the time when the motion begins. The phase constant allows us to describe the initial conditions of the motion and is needed to fully describe the behavior of the system.
Example:
- Consider a mass attached to a spring and undergoing simple harmonic motion. If the phase constant is 0, it means that the object starts at its equilibrium position. If the phase constant is π/2, it means that the object starts at the maximum displacement in the positive direction. Similarly, a phase constant of -π/2 means that the object starts at the maximum displacement in the negative direction.
Phase difference:
Phase difference refers to the difference in phase between two oscillating objects. It is denoted by ΔΦ and is used to describe the relative positions of the objects at a given point in time. The phase difference can be positive or negative and is measured in radians.
Example:
- If two objects are in phase, it means that they have the same phase angle at a given time. If two objects are out of phase by π/2, it means that one object is at its maximum displacement while the other is at its equilibrium position.
Understanding the phase and phase constant is crucial in analyzing and predicting the behavior of systems undergoing simple harmonic motion. These concepts allow us to describe the starting conditions of the motion and determine the positions of multiple objects in relation to each other.
Simple Harmonic Oscillator
A simple harmonic oscillator is a system that undergoes simple harmonic motion (SHM), which is a type of periodic motion where the restoring force is directly proportional to the displacement of the object from its equilibrium position and acts in the opposite direction. The motion of a simple harmonic oscillator can be described by a sinusoidal function, such as sine or cosine.
An important characteristic of a simple harmonic oscillator is its period, which is the time taken for one complete cycle of motion. The period of an oscillator is inversely proportional to its frequency, which is the number of cycles per unit time. The frequency is measured in hertz (Hz).
The displacement of a simple harmonic oscillator is usually represented by the variable x. The maximum displacement from the equilibrium position is called the amplitude of the oscillator. The amplitude is determined by the initial conditions of the system and remains constant throughout the motion.
The angular frequency is another important characteristic of a simple harmonic oscillator. It is denoted by the symbol ω and represents the rate at which the phase of the oscillation changes. The angular frequency is related to the frequency of the oscillator by the equation ω = 2πf, where f is the frequency.
In addition to the displacement, other parameters of a simple harmonic oscillator include the velocity (v) and the acceleration (a). The velocity is the rate of change of displacement, while the acceleration is the rate of change of velocity. Both the velocity and acceleration of a simple harmonic oscillator are sinusoidal functions of time and have specific phase relationships with the displacement.
In summary, a simple harmonic oscillator is a system that undergoes simple harmonic motion, characterized by a harmonic oscillation of displacement, velocity, and acceleration. The motion is determined by parameters such as the period, amplitude, frequency, and angular frequency. Understanding the behavior of simple harmonic oscillators is essential for analyzing various physical systems, including pendulums, mass-spring systems, and vibrating objects.
Spring-Mass System
In the study of simple harmonic motion, one commonly encountered system is the spring-mass system. This system consists of a mass attached to a spring, which is usually fixed at one end. The mass is free to move in one direction along a straight line. This system is often used as a model for various real-life situations, such as the motion of a weight hanging from a spring or the oscillation of a car suspension.
When a spring-mass system is in equilibrium, the spring is neither stretched nor compressed, and the mass is at its rest position. In this state, the spring exerts a force on the mass equal in magnitude but opposite in direction to the gravitational force acting on the mass. As a result, the system remains stationary.
However, if the mass is displaced from its equilibrium position, the spring will experience a restoring force that pulls the mass back towards the equilibrium. This force is proportional to the displacement and acts in the opposite direction. The equation that describes the motion of the spring-mass system is known as Hooke’s Law.
Hooke’s Law states that the force exerted by the spring is directly proportional to the displacement of the mass from its equilibrium position. This can be expressed mathematically as F = -kx, where F is the force, k is the spring constant, and x is the displacement. The negative sign indicates that the force is in the opposite direction of the displacement.
By solving the equation of motion derived from Hooke’s Law, one can determine the behavior of the spring-mass system. It is found that the mass undergoes simple harmonic motion, oscillating back and forth around the equilibrium position. The frequency of the oscillation depends on the properties of the system, such as the mass and the spring constant.
In conclusion, the spring-mass system is an important concept in the study of simple harmonic motion. By understanding the behavior of this system, we can gain insights into various real-life phenomena and utilize this knowledge in practical applications.