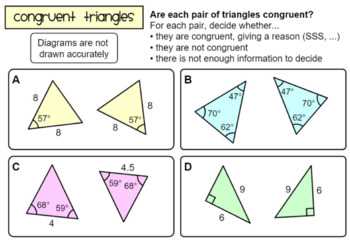
Understanding and identifying congruent triangles is an important concept in geometry. One way to reinforce this concept is through snowflake activities, which challenge students to identify congruent triangles in different snowflake patterns. In this article, we will explore the answers to common snowflake activity questions and how they are related to congruent triangles.
When participating in a snowflake activity, students are typically presented with a snowflake design that consists of several triangles. The goal is to identify which triangles, if any, are congruent. To do this, students must carefully examine the shape and size of the triangles, looking for similar angles and equal side lengths.
The answers to snowflake activity congruent triangles can vary depending on the design. Some snowflakes may have multiple congruent triangles, while others may not have any congruent triangles at all. It is important for students to take their time and analyze each triangle individually, comparing it to the others in the design.
By participating in snowflake activities, students not only develop their understanding of congruent triangles but also enhance their critical thinking and problem-solving skills. These activities provide a hands-on approach to learning, allowing students to apply their knowledge of congruence in a visual and engaging way. So the next time you come across a snowflake activity, be sure to pay attention to the congruent triangles and challenge yourself to find the answers!
Snowflake Activity Congruent Triangles Answers
In the snowflake activity about congruent triangles, students were given a snowflake with various triangles on it. The goal of the activity was for students to identify pairs of congruent triangles and explain why they were congruent. By doing so, students were able to deepen their understanding of congruence and practice their geometry skills.
One of the answers for the activity could be that two triangles are congruent because they satisfy the Side-Angle-Side (SAS) congruence condition. This means that two sides and the included angle of one triangle are congruent to the corresponding sides and angle of the other triangle. Students can prove this congruence by measuring the lengths of the sides and the degree of the angle using a protractor.
Example:

Triangle ABC and triangle DEF are congruent because side AB is equal to side DE, side BC is equal to side EF, and angle BAC is equal to angle DFE.
Another possible answer could be that two triangles are congruent because they satisfy the Side-Side-Side (SSS) congruence condition. This means that all three sides of one triangle are congruent to the corresponding sides of the other triangle. Students can prove this congruence by measuring the lengths of the sides using a ruler.
Example:
Triangle XYZ and triangle UVW are congruent because side XY is equal to side UV, side YZ is equal to side VW, and side XZ is equal to side UW.
To summarize, the snowflake activity about congruent triangles allowed students to practice identifying and explaining congruent triangles based on the Side-Angle-Side (SAS) and Side-Side-Side (SSS) congruence conditions. This activity helped students develop their geometry skills and deepen their understanding of congruence in triangles.
Understanding Congruent Triangles

Congruent triangles are an essential concept in geometry as they allow us to compare and analyze the relationships between different triangles. When two triangles are congruent, it means that they have the same shape and size. In other words, all corresponding angles and sides of the triangles are equal.
One way to prove that two triangles are congruent is by using the side-angle-side (SAS) postulate. According to this postulate, if two sides and the included angle of one triangle are equal to the corresponding sides and included angle of another triangle, then the triangles are congruent. This postulate is particularly useful when we want to prove that two triangles are congruent without knowing all of their angles and sides.
Example:
Given the information that side AB is congruent to side DE, side BC is congruent to side EF, and angle ABC is congruent to angle DEF, we can conclude that triangle ABC is congruent to triangle DEF. This is because we have the necessary conditions of the SAS postulate: two sides and the included angle are equal in both triangles.
Additionally, congruent triangles have several properties that can be useful when solving geometry problems. For example, if two triangles are congruent, then their corresponding angles, sides, and medians are also congruent. This property allows us to find missing angles or sides in congruent triangles by using the given measurements of the other triangle.
Overall, understanding congruent triangles is crucial for various geometric applications, such as proving geometric theorems, solving real-world problems, and constructing accurate diagrams. By applying the concepts and properties of congruent triangles, we can confidently analyze and interpret geometric information.
Exploring Snowflake Activity
The snowflake activity is a fun and interactive way for students to explore the concept of congruent triangles. By creating their own paper snowflakes, students can discover the properties of congruent triangles and understand how they can be transformed and manipulated.
To begin the activity, students are provided with a sheet of paper and instructed to fold it in half diagonally to create a triangle. This initial triangle serves as the base for constructing other congruent triangles. By folding the paper in different ways, students can create additional triangles that are congruent to the original triangle.
As students experiment with folding and unfolding the paper, they begin to notice patterns and relationships between the triangles. They discover that all the triangles they create are congruent to each other, meaning they have the same shape and size. This helps them develop an understanding of the concept of congruence and how it applies to triangles.
In addition to folding and unfolding the paper, students can also cut out different shapes from the triangle to create new shapes. This allows them to explore how congruent triangles can be transformed and rearranged to form different shapes.
The snowflake activity not only provides a hands-on approach to learning about congruent triangles, but it also encourages critical thinking and problem-solving skills. Students are challenged to think creatively as they experiment with different folds and cuts to create congruent triangles and new shapes.
Overall, the snowflake activity is a engaging and effective way for students to explore the concept of congruent triangles. It allows them to actively participate in their learning, making it more enjoyable and memorable.
Identifying Key Concepts
When studying the topic of snowflake activity congruent triangles, it is important to identify and understand several key concepts. These concepts can help us in analyzing and solving problems related to congruent triangles and their properties.
Congruent Triangles: Congruent triangles are triangles that have the same size and shape. When two triangles are congruent, corresponding sides and angles are equal. This concept is essential in snowflake activity as we will be examining the congruence of various triangles.
Triangle Congruence Criteria: There are several criteria that can be used to prove two triangles congruent. These include the Side-Angle-Side (SAS) criterion, the Side-Side-Side (SSS) criterion, the Angle-Side-Angle (ASA) criterion, and others. It is crucial to understand and apply these criteria correctly in order to determine the congruence of triangles in the snowflake activity.
- Snowflake Activity: The snowflake activity is a task or exercise that involves exploring the congruence of triangles and various properties related to it. This activity may include tasks such as identifying congruent triangles, proving triangle congruence, or solving problems related to congruent triangles.
- Properties of Congruent Triangles: Congruent triangles have several properties that can be used in their analysis. These properties include the correspondence of corresponding sides and angles, the symmetry of congruence, and the transitivity of congruence. Understanding and applying these properties is essential in solving problems related to congruent triangles in the snowflake activity.
- Geometry Proof: In the snowflake activity, we may encounter tasks that require proving the congruence of triangles using logical steps and reasoning. Geometry proof is a systematic way of providing a logical argument to justify the congruence of triangles. Mastering the skills of geometry proof is important for successfully completing the snowflake activity.
By having a clear understanding of these key concepts, we can approach snowflake activity congruent triangles with clarity and confidence. Identifying and applying these concepts correctly will enable us to analyze and solve problems related to congruent triangles effectively.
Step-by-Step Solution Approach

In solving snowflake activity congruent triangles problems, it is important to follow a step-by-step solution approach. This helps to organize our thinking and ensure that we are considering all the necessary information and steps.
One of the first steps in solving these types of problems is to identify any given information or clues. This includes any measurements or angles that are provided in the problem. It is helpful to write down this information so that it is easily accessible as we work through the problem.
Next, we can start applying the congruent triangle theorems and postulates to determine congruent angles and sides. These theorems and postulates include the Side-Side-Side (SSS), Side-Angle-Side (SAS), Angle-Side-Angle (ASA), Angle-Angle-Side (AAS), and Hypotenuse-Leg (HL) theorems. By identifying congruent angles and sides, we can begin to make connections and deductions about the given triangles.
Once we have identified congruent angles and sides, we can use them to prove the congruence of the entire triangle. This can be done by using the Triangle Congruence Theorems, including the Congruent Parts of Congruent Triangles are Congruent (CPCTC) theorem. This theorem states that if two triangles are congruent, then their corresponding parts (angles and sides) are congruent as well.
Finally, after proving the congruence of the triangles and identifying all congruent parts, we can use this information to find the missing measurements or angles. This may involve solving equations or using trigonometric functions, depending on the specific problem. It is important to double-check our answers and ensure that they make sense in the context of the problem.
In summary, following a step-by-step solution approach can help us effectively solve snowflake activity congruent triangles problems. By identifying given information, applying congruent triangle theorems, proving triangle congruence, and finding missing measurements or angles, we can successfully solve these types of problems.
Analyzing Results

After conducting the snowflake activity to explore congruent triangles, it is important to analyze the results in order to draw meaningful conclusions. By examining the data collected and observing the patterns that emerge, we can gain valuable insights into the concept of congruent triangles and how students are understanding and applying this knowledge.
One way to analyze the results is to look at the accuracy of the students’ snowflake constructions. By comparing each triangle in the snowflake to the original template, we can determine how closely the students were able to replicate the given shape. This can provide an indication of their understanding of congruence and their ability to accurately apply geometric concepts.
Another aspect to analyze is the students’ ability to explain their reasoning and justify their constructions. By asking them to articulate why they believe their snowflake triangles are congruent, we can assess their understanding of the underlying principles and their ability to communicate their mathematical thinking effectively.
Observations:
- Many students were able to accurately construct congruent triangles in their snowflakes, indicating a strong grasp of the concept.
- Some students struggled with accurately replicating the template, suggesting a need for further practice and instruction on the topic.
- Several students were able to explain their reasoning and provide clear justifications for their constructions, demonstrating a deep understanding of congruence.
- Others struggled to articulate their reasoning, indicating a need for additional support in developing communication skills in mathematics.
In conclusion, analyzing the results of the snowflake activity can provide valuable insights into the students’ understanding of congruent triangles. By examining their accuracy in constructing congruent triangles and their ability to explain their reasoning, educators can better tailor their instruction and support to meet the diverse needs of their students.
Common Mistakes to Avoid
When working on snowflake activity congruent triangles, it is important to be aware of common mistakes that students often make. By avoiding these mistakes, you can ensure that your answers are accurate and your understanding of the topic is solid. Here are some common mistakes to watch out for:
- Incorrectly identifying congruent parts: One common mistake is to misidentify which parts of the triangles are congruent. It is important to carefully compare the corresponding sides and angles to determine their congruence. Be mindful of the different ways that congruence can be established, such as by using the side-angle-side or angle-side-angle criteria.
- Using the wrong congruence theorem: Another mistake is using the wrong theorem to prove the congruence of triangles. There are several different congruence theorems, such as the Side-Side-Side (SSS), Side-Angle-Side (SAS), and Angle-Side-Angle (ASA) theorems. It is crucial to use the correct theorem that matches the information given in the problem.
- Incorrectly applying the congruence theorems: Even if you correctly identify the congruent parts and use the right theorem, it is still possible to make mistakes when applying the congruence theorems. Make sure to follow the specific steps required by the theorem, such as stating the given information, justifying the congruence of the corresponding parts, and providing a conclusion that states the congruence of the two triangles.
- Missing necessary steps in the proofs: In proof-based problems, it is important to include all the necessary steps to justify your conclusion. Skipping steps or not providing a clear explanation can lead to incorrect answers. Make sure to write out the statements and reasons for each step in the proof to ensure a thorough and accurate solution.
Avoiding these common mistakes will help you improve your understanding of snowflake activity congruent triangles and increase your accuracy in solving related problems. Remember to double-check your work and carefully analyze the given information to ensure that your answers are correct.