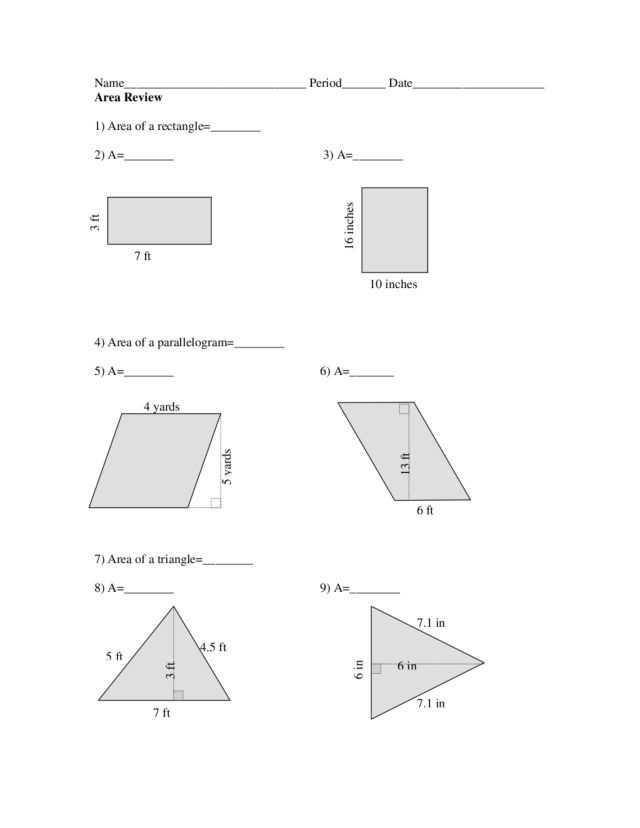
In geometry, parallelograms are a special type of quadrilateral with unique properties and characteristics. Understanding these properties is crucial for solving problems related to their measurements and dimensions. This article provides an answer key to some common questions about special parallelograms, including rectangles, squares, and rhombi.
Rectangles are parallelograms with four right angles. They have equal opposite sides and are a special case of a parallelogram. The answer key for rectangles includes explanations on finding their area, perimeter, and diagonal lengths. Additionally, the key covers how to identify rectangles by their side lengths and relationships between angles.
Squares, on the other hand, are parallelograms with four equal sides and four right angles. The special properties of squares make them particularly interesting. The answer key for squares includes details on finding their area, perimeter, and diagonal lengths. It also covers concepts such as the Pythagorean theorem and the relationship between the side length and diagonal length of a square.
Rhombi are parallelograms with four equal sides but without right angles. They are a unique type of parallelogram that requires a different approach to solve problems. The answer key for rhombi includes explanations on finding their area, perimeter, and diagonals. Additionally, it covers concepts like the relationship between the side length and diagonal length of a rhombus and how to determine if a shape is a rhombus or not.
Definition of a parallelogram
A parallelogram is a four-sided polygon with opposite sides that are parallel and congruent. This means that the opposite sides of a parallelogram are always the same length and do not intersect.
Another important characteristic of a parallelogram is that its opposite angles are congruent. This means that the angles formed by the intersection of the opposite sides of a parallelogram are always equal in measure.
One way to visually identify a parallelogram is by looking at its shape. A parallelogram has two pairs of parallel sides, meaning that each pair of opposite sides is parallel to each other. In addition, the pairs of opposite angles in a parallelogram are also congruent.
The properties of a parallelogram make it a versatile shape that is useful in various mathematical and practical applications. For example, the properties of a parallelogram are often used in geometry to calculate the area and perimeter of the shape. In engineering and architecture, parallelograms are frequently encountered in the design and construction of structures. Overall, the definition of a parallelogram provides a foundation for studying and understanding the properties and characteristics of this important geometric shape.
Properties of a parallelogram
A parallelogram is a quadrilateral with two pairs of parallel sides. This unique shape has several properties that set it apart from other quadrilaterals.
Opposite sides are congruent: In a parallelogram, opposite sides are always equal in length. This means that if we take any two sides that are not adjacent to each other and measure them, we will get the same result.
Opposite angles are congruent: Another property of a parallelogram is that the opposite angles are always congruent. This means that if we take any two angles that are not adjacent to each other and measure them, we will get the same angle measure.
Diagonals bisect each other: The diagonals of a parallelogram intersect each other at their midpoints. This means that if we draw the diagonals of a parallelogram, they will divide each other into two equal parts.
Consecutive angles are supplementary: The consecutive angles in a parallelogram are always supplementary, meaning that they add up to 180 degrees. This property holds true for any pair of angles that are next to each other and share a side.
Opposite sides are parallel: As the name suggests, all four sides of a parallelogram are parallel to each other. This means that the opposite sides will never intersect, no matter how the parallelogram is oriented.
These are just a few of the key properties of a parallelogram. Understanding these properties can help us solve problems involving the angles, sides, and diagonals of parallelograms.
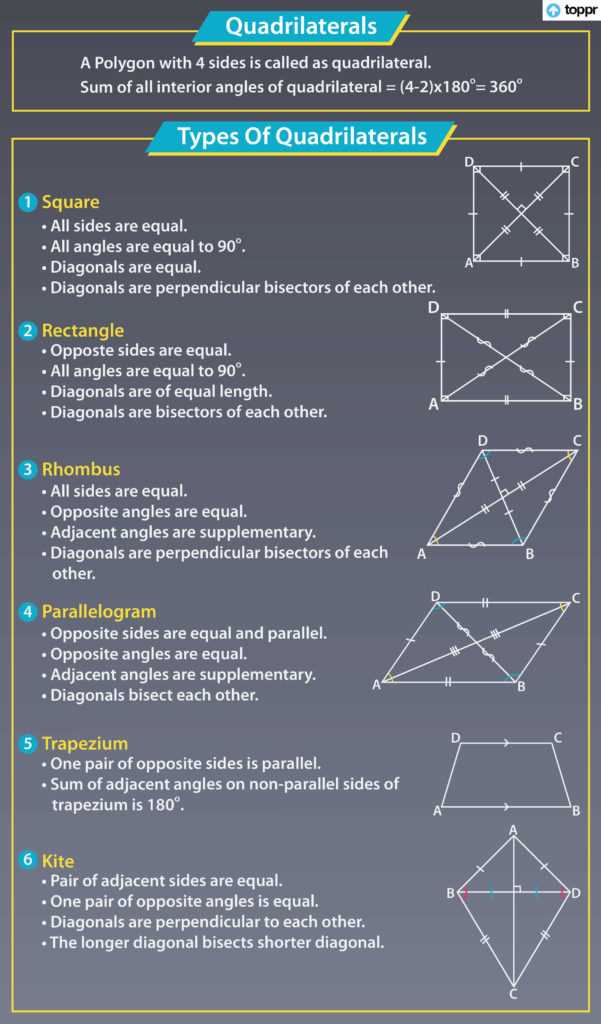
Special types of parallelograms
Parallelograms are quadrilaterals with opposite sides parallel and equal in length. They have several special properties that distinguish them from other quadrilaterals.
One special type of parallelogram is a rectangle. A rectangle is a parallelogram with all angles equal to 90 degrees. This means that the opposite sides of a rectangle are equal in length, and the diagonals bisect each other. Rectangles have several unique properties, such as the fact that their diagonals are congruent and they have perpendicular diagonals.
Another special type of parallelogram is a square. A square is a parallelogram with all sides equal in length and all angles equal to 90 degrees. Like rectangles, squares have congruent diagonals and perpendicular diagonals. In addition, squares have other unique properties, such as the fact that all their sides are equal in length and their diagonals are equal and perpendicular bisectors of each other.
A rhombus is yet another special type of parallelogram. A rhombus is a parallelogram with all sides equal in length. Like squares and rectangles, rhombuses have congruent diagonals and perpendicular diagonals. However, rhombuses do not have right angles. Instead, their angles are typically acute or obtuse.
In conclusion, parallelograms come in various special types, each with its own unique properties. Rectangles, squares, and rhombuses are just a few examples of special parallelograms that have distinct characteristics and valuable applications in geometry and other areas of mathematics.
Definition of a rectangle

A rectangle is a type of parallelogram that has several unique properties. It is a quadrilateral with four sides that are all congruent in length, forming right angles at each vertex. The opposite sides of a rectangle are parallel and equal in length, and the diagonals divide the rectangle into two congruent right triangles.
The four angles of a rectangle are all right angles, which means they measure 90 degrees each. This property makes rectangles especially useful in construction and design, as right angles are often needed for stability and precision. Additionally, the sum of the interior angles of a rectangle is always 360 degrees, making it a closed shape.
Key Features of a Rectangle:
- All four sides are congruent in length
- Opposite sides are parallel and equal in length
- All four angles measure 90 degrees
- Diagonals are congruent, dividing the rectangle into two congruent right triangles
- Sum of the interior angles is 360 degrees
The formula for finding the area of a rectangle is length x width. The perimeter of a rectangle is calculated by adding the lengths of all four sides together.
| Shape | Definition | Properties |
|---|---|---|
| Rectangle | A quadrilateral with four congruent sides, right angles, and parallel opposite sides | All sides are congruent in length, opposite sides are parallel and equal in length, all angles measure 90 degrees, diagonals divide the rectangle into congruent right triangles, sum of interior angles is 360 degrees |
A rectangle is a special type of parallelogram that has several unique properties. One of the primary properties of a rectangle is that it has four right angles. This means that each of the interior angles of a rectangle measures 90 degrees. The presence of right angles in a rectangle is what distinguishes it from other parallelograms.
In addition to its right angles, a rectangle also has opposite sides that are equal in length. This means that the length of one side of a rectangle is equal to the length of the side that is opposite to it. In other words, if AB and CD are two sides of a rectangle, then AB = CD.
Another property of a rectangle is that it has two pairs of parallel sides. This means that the opposite sides of a rectangle are parallel to each other. The presence of parallel sides in a rectangle allows it to have equal opposite angles. This means that if angle A is equal to angle C, then angle B is equal to angle D.
Overall, the properties of a rectangle make it a unique and distinct shape. Its right angles, equal sides, and parallel sides set it apart from other parallelograms and contribute to its usefulness in many mathematical and real-world applications.
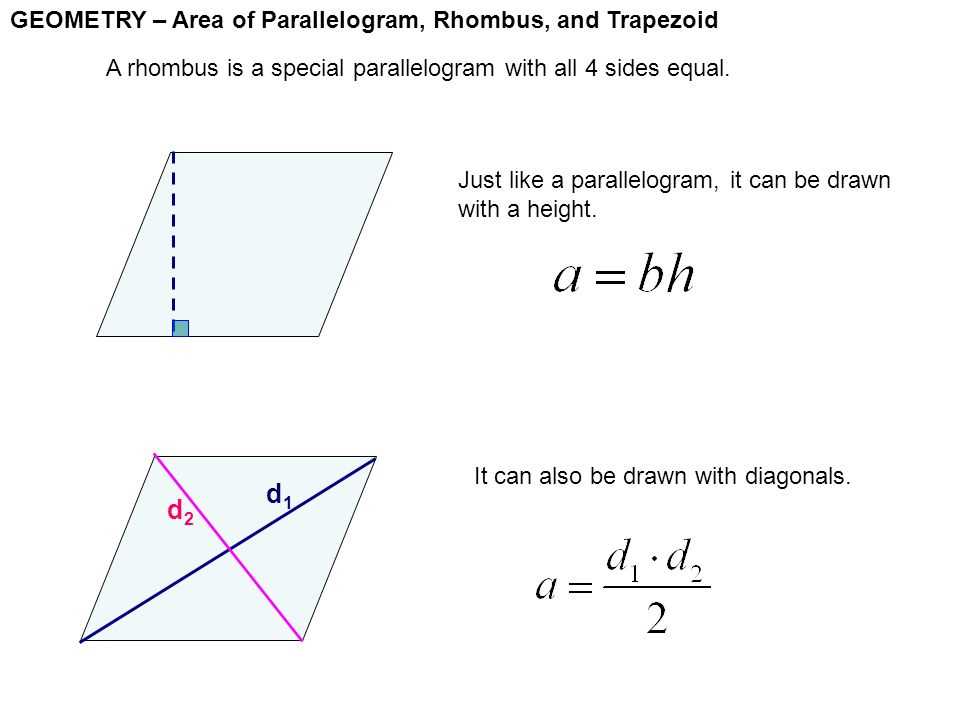
Definition of a rhombus
A rhombus is a special type of quadrilateral that has several defining characteristics. First and foremost, a rhombus is a parallelogram, which means that opposite sides of the shape are parallel. In addition, all four sides of a rhombus are congruent, or equal in length. This makes it different from a rectangle or square, where only opposite sides are equal.
Another important feature of a rhombus is that its angles are all congruent. This means that all four angles of a rhombus are equal in measure. Since the opposite angles of a parallelogram are also congruent, this means that a rhombus has two pairs of opposite congruent angles.
A rhombus can be thought of as a type of square that has been “squished” or stretched in a specific way. While all sides of a square are equal in length and all angles are right angles, a rhombus still has equal sides but its angles can be any measure that adds up to 360 degrees, as long as they are all equal.
Overall, a rhombus is a special parallelogram that has congruent sides and congruent angles. It is a unique shape that combines the properties of a parallelogram, rectangle, and square. Understanding the definition of a rhombus is important in geometry and can help in solving problems involving this shape.
Properties of a Rhombus
A rhombus is a special type of parallelogram that has several unique properties. One of the defining characteristics of a rhombus is that all four sides are equal in length. This means that the opposite sides of a rhombus are parallel and congruent. The equal side lengths give the rhombus its distinct diamond shape.
Another important property of a rhombus is that its opposite angles are congruent. This means that the angles formed by the intersection of the diagonals of a rhombus are equal in measure. The diagonals of a rhombus also bisect each other at right angles, creating four right angles at the point of intersection.
A rhombus can also be thought of as a special case of a kite, where all four sides are congruent. Because of its symmetrical and regular shape, a rhombus has rotational symmetry of order 2. This means that it can be rotated 180 degrees about its center and still appear the same.
In summary, the properties of a rhombus include equal side lengths, congruent opposite angles, perpendicular bisecting diagonals, and rotational symmetry of order 2. These properties make the rhombus a unique and interesting shape in the world of geometry.