
Statistics Exam 3 is an important assessment that measures a student’s understanding of statistical concepts and their ability to apply them in various scenarios. This exam covers a wide range of topics including probability, hypothesis testing, confidence intervals, and regression analysis.
During the exam, students will be required to solve complex statistical problems, analyze and interpret data, and make informed decisions based on statistical findings. Proficiency in utilizing statistical software such as SPSS or R may also be evaluated.
Successful completion of Statistics Exam 3 demonstrates a student’s competency in statistical analysis and their ability to utilize statistical tools to solve real-world problems. This exam plays a crucial role in assessing a student’s understanding of statistical concepts and their readiness to apply these skills in their academic and professional endeavors.
What is Statistics Exam 3?
Statistics Exam 3 is an assessment that evaluates students’ understanding and application of statistical concepts and techniques. It serves as a benchmark to measure their knowledge and proficiency in this field of study. Exam 3 typically covers advanced topics in statistics and requires students to demonstrate their ability to analyze data, interpret results, and draw meaningful conclusions.
During Statistics Exam 3, students are often tested on their proficiency in areas such as hypothesis testing, confidence intervals, regression analysis, and analysis of variance. They are expected to apply these statistical techniques to real-world scenarios and datasets, making connections between theory and practice. The exam may consist of a combination of multiple-choice questions, problem-solving tasks, and data analysis exercises, allowing students to showcase their quantitative skills and critical thinking abilities.
Throughout the exam, it is essential for students to accurately interpret statistical output, understand the assumptions underlying different statistical tests, and effectively communicate their findings. They need to demonstrate their ability to select the appropriate statistical methods based on the research question and dataset, as well as justify their choices using statistical reasoning.
Overall, Statistics Exam 3 serves as a comprehensive assessment of students’ knowledge and application of statistical concepts. It provides an opportunity for them to demonstrate their understanding of advanced statistical techniques and their ability to apply them in practical situations. By successfully completing Exam 3, students showcase their proficiency in statistics, which is crucial for further academic and professional pursuits in fields such as research, data analysis, and decision-making.
Understanding the purpose
The purpose of the statistics exam is to assess the knowledge and understanding of key statistical concepts and techniques. This exam is typically taken by students studying statistics or related fields, who need to demonstrate their proficiency in the subject. The exam aims to measure the student’s ability to apply statistical methods and interpret the results in order to make informed decisions and draw conclusions.
During the exam, students are tested on various statistical topics such as probability, hypothesis testing, regression analysis, and data visualization. They are expected to demonstrate their understanding of these topics by solving problems, answering questions, and providing logical explanations. The purpose of the exam is to evaluate the student’s ability to critically analyze data, identify the appropriate statistical techniques to use, and apply them correctly to solve real-world problems.
The exam also evaluates the student’s ability to interpret statistical results and communicate them effectively. Students are often required to interpret statistical output, draw conclusions, and make recommendations based on the data analysis. This demonstrates their understanding of how statistical techniques can be used to support decision-making processes in various fields such as business, healthcare, social sciences, and more.
Furthermore, the statistics exam aims to assess the student’s mathematical and computational skills. Students are often required to perform calculations, manipulate data, and use statistical software or programming languages to analyze and visualize data. These skills are important for conducting statistical analysis and are highly valued in data-driven industries.
In summary, the purpose of the statistics exam is to evaluate the student’s knowledge and understanding of key statistical concepts, their ability to apply statistical techniques, interpret results, and effectively communicate findings. By successfully passing the exam, students demonstrate their proficiency in statistics and their readiness to apply statistical methods in real-world scenarios.
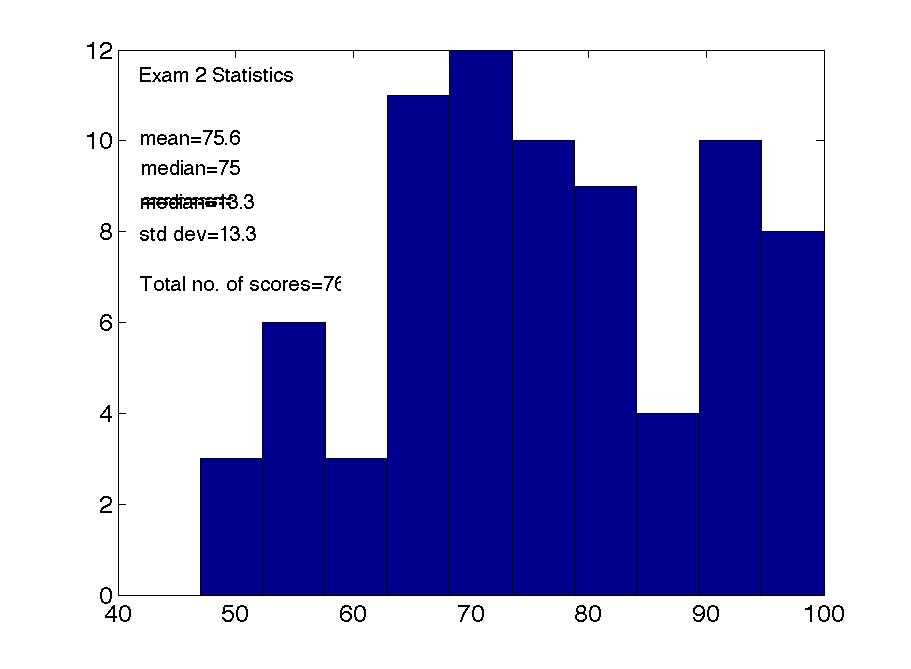
Important topics for Statistics Exam 3
In Statistics Exam 3, students will be tested on a variety of important topics covered throughout the course. Familiarity with these topics is essential for success in the exam. Here are some of the key topics that students should focus on:
1. Central Limit Theorem: Understanding and applying the Central Limit Theorem is crucial for analyzing and interpreting data. Students should be able to explain the concept, calculate the standard error, and use it to make inferences about population means.
2. Hypothesis Testing: Hypothesis testing is a fundamental concept in statistics. Students should be familiar with the steps involved in hypothesis testing, including defining null and alternative hypotheses, choosing an appropriate significance level, conducting the test, and interpreting the results.
3. Confidence Intervals: Confidence intervals are used to estimate population parameters based on sample data. Students should be able to calculate and interpret confidence intervals for means and proportions, and understand the relationship between confidence level and the width of the interval.
4. Regression Analysis: Regression analysis involves studying the relationship between a dependent variable and one or more independent variables. Students should be able to perform regression analysis, interpret the coefficient estimates, and assess the goodness of fit.
5. ANOVA: Analysis of Variance (ANOVA) is used to compare the means of three or more groups. Students should be familiar with the different types of ANOVA (one-way, two-way), understand the assumptions of ANOVA, and be able to interpret the results.
6. Chi-Square Test: The chi-square test is used to analyze categorical data and determine if there is a significant association between variables. Students should know how to conduct a chi-square test, interpret the results, and understand the limitations of the test.
These topics are not exhaustive, but they represent some of the most important concepts that students should prioritize in their exam preparation. It is recommended to review class notes, practice solving problems, and seek additional resources to enhance understanding and proficiency in these areas.
Descriptive statistics
Descriptive statistics is a branch of statistics that focuses on summarizing and describing the main features of a dataset. It involves examining and analyzing the data to understand its characteristics and distributions. Descriptive statistics provides an overview of the data, allowing researchers and analysts to identify patterns, trends, and relationships.
One of the key measures used in descriptive statistics is central tendency, which includes mean, median, and mode. These measures help to identify the average or typical value of a dataset. Mean is calculated by summing all the values and dividing by the total count, while median represents the middle value when the data is sorted in ascending order. Mode, on the other hand, is the value that appears most frequently in the dataset.
Another important aspect of descriptive statistics is dispersion, which measures the spread or variability of the data. Measures of dispersion include range, variance, and standard deviation. Range is the difference between the maximum and minimum values in the dataset, while variance and standard deviation provide information about the average deviation from the mean. A larger standard deviation indicates a higher degree of dispersion in the data.
Summary measures
In addition to central tendency and dispersion, descriptive statistics also includes other summary measures such as quartiles, percentiles, and interquartile range. Quartiles divide the dataset into four equal parts, while percentiles represent the position of a specific value in relation to the whole dataset. Interquartile range measures the spread of the middle 50% of the data and is calculated as the difference between the third quartile and the first quartile.
Visual representation
Descriptive statistics can be further enhanced through visual representation. Graphs and charts such as histograms, box plots, and scatter plots provide a visual summary of the data, making it easier to interpret and understand. These visual representations help to identify outliers, explore the shape of distributions, and detect any patterns or trends in the data.
In conclusion, descriptive statistics plays a crucial role in analyzing and summarizing data. It provides essential information about the characteristics, central tendency, dispersion, and other aspects of the dataset. Additionally, visual representation enhances the understanding of the data by providing a visual summary of the information. Descriptive statistics is an essential tool for researchers, analysts, and decision-makers to gain insights and make informed decisions based on the available data.
Probability concepts
Probability is a fundamental concept in statistics that allows us to quantify the likelihood of an event occurring. It is a measure of uncertainty and plays a crucial role in various statistical calculations and analyses. In order to understand probability, it is important to grasp the concept of a sample space, which consists of all possible outcomes of an experiment or event. For example, in rolling a fair six-sided die, the sample space would be {1, 2, 3, 4, 5, 6}. Each outcome in the sample space has a certain probability associated with it.
Probability can be expressed as a number between 0 and 1, where 0 represents an impossible event and 1 represents a certain event. The probability of an event A, denoted as P(A), is calculated by dividing the number of favorable outcomes by the total number of possible outcomes. This can be written as:
P(A) = Number of favorable outcomes / Total number of possible outcomes
There are different types of probabilities, such as theoretical, empirical, and subjective. Theoretical probability is based on mathematical principles and is often used in simple experiments with equally likely outcomes. Empirical probability is based on observed data and is calculated by conducting experiments or collecting data. Subjective probability, on the other hand, is based on personal judgment or beliefs.
In addition to calculating probabilities, it is important to understand basic probability concepts such as complement, union, and intersection. The complement of an event A, denoted as A’, is the probability of A not occurring. The union of two events A and B, denoted as A ∪ B, is the probability of either A or B occurring. The intersection of two events A and B, denoted as A ∩ B, is the probability of both A and B occurring simultaneously.
Probability concepts are widely used in various fields, including finance, engineering, sports, and medical research. They provide a framework for making informed decisions and predictions based on available data and information. By understanding probability concepts, individuals can better interpret and analyze data, and make more accurate conclusions and predictions.
Statistical distributions
In statistics, a distribution refers to the way in which data values are spread out or distributed across a dataset. Different statistical distributions have different characteristics and are used to model various types of data. Understanding these distributions is crucial in data analysis and decision-making processes.
One commonly used distribution is the normal distribution, also known as the Gaussian distribution or the bell curve. It is symmetrical and bell-shaped, with a peak at the mean and a standard deviation that determines the spread. The normal distribution is often used to represent real-world phenomena, such as heights or test scores, that tend to cluster around a central value.
Another important distribution is the binomial distribution, which models the probability of getting a specific number of successes in a fixed number of independent Bernoulli trials. It is characterized by two parameters: the number of trials and the probability of success. The binomial distribution is frequently used in experimental studies or surveys to analyze binary outcomes, such as the success or failure of a certain event.
The exponential distribution is another widely used distribution, often employed to model the time between rare events or the lifetime of certain products. It is characterized by a single parameter, the rate parameter, which determines the average time between events. The exponential distribution is commonly used in reliability analysis or queueing theory.
In addition to these, there are many other statistical distributions, such as the Poisson distribution, the chi-square distribution, and the t-distribution, each with its own characteristics and applications in different fields of study. Understanding the properties and applications of these distributions can help statisticians and data analysts in making valid inferences and drawing meaningful conclusions from data.
Hypothesis Testing
Hypothesis testing is a crucial tool in statistical analysis that allows us to make inferences about populations based on sample data. It involves setting up a null hypothesis and an alternative hypothesis, collecting data, and using statistical tests to determine the likelihood of the null hypothesis being true.
The null hypothesis is a statement that assumes there is no significant difference or relationship between variables. The alternative hypothesis, on the other hand, suggests that there is indeed a significant difference or relationship. The objective of hypothesis testing is to either accept or reject the null hypothesis based on the evidence provided by the data.
To conduct a hypothesis test, we typically use test statistics, such as the t-test or chi-square test, depending on the type of data and research question. These test statistics calculate the probability of observing the obtained data under the assumption that the null hypothesis is true. If this probability, known as the p-value, is less than a predetermined significance level (usually 0.05), we reject the null hypothesis and accept the alternative hypothesis.
Hypothesis testing allows researchers and analysts to draw meaningful conclusions about population parameters based on the data they have collected. It provides a systematic and objective approach to decision-making, enabling us to validate or reject assumptions and theories, and make informed decisions based on the evidence.
In summary, hypothesis testing is a powerful tool that helps us make inferences about populations based on sample data. By setting up null and alternative hypotheses, collecting and analyzing data using statistical tests, and interpreting the results, we can draw valid conclusions and make informed decisions. It is an integral part of statistical analysis and is used in a wide range of fields, such as medicine, social sciences, and business.