In order to investigate this question, the researcher has collected a sample of individuals and obtained information on their preferences. The next step is to conduct a hypothesis test to determine if the proportion of individuals who prefer Option A is significantly different from the proportion who prefer Option B.
The researcher will define two hypotheses: the null hypothesis, which states that there is no significant difference between the proportions of individuals who prefer Option A and Option B, and the alternative hypothesis, which states that there is a significant difference.
The researcher will then calculate a test statistic, typically the z-score, and compare it to a critical value to determine the statistical significance of the results. If the test statistic falls in the rejection region, the researcher will reject the null hypothesis and conclude that there is a significant difference in preferences between Option A and Option B.
This hypothesis test is important because it allows the researcher to make inferences about a larger population based on the sample data collected. By determining if there is a significant difference in preferences, the researcher can provide valuable insights that can inform decision-making and improve the effectiveness of marketing strategies or product design.
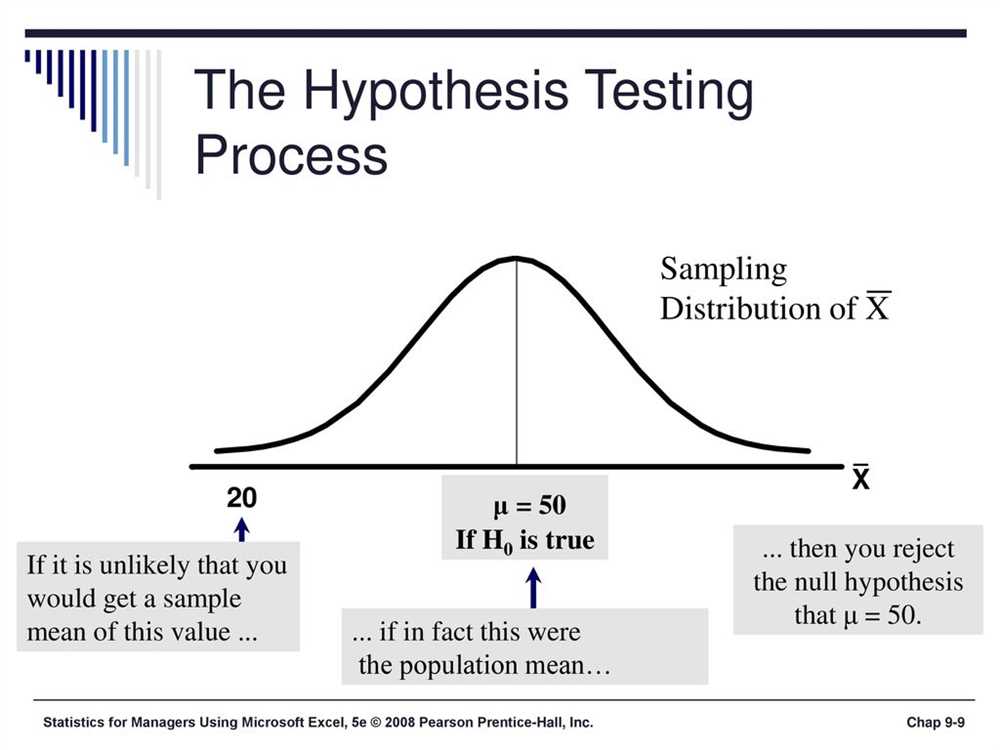
Understanding a single-sample hypothesis test
Introduction
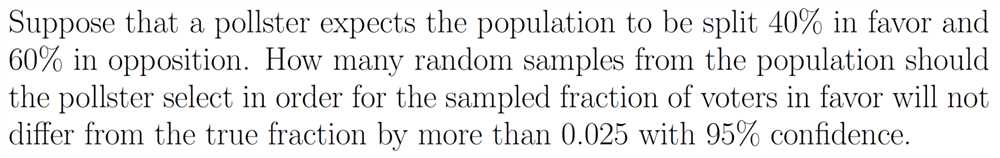
A single-sample hypothesis test is a statistical procedure used to determine whether the mean of a single sample is significantly different from a hypothesized value. This type of test is commonly used in research and data analysis to make conclusions about a population based on a sample.
The process
The process of conducting a single-sample hypothesis test involves several steps. First, the researcher must define the null hypothesis and the alternative hypothesis. The null hypothesis is the assumption that there is no significant difference between the sample mean and the hypothesized value, while the alternative hypothesis is the opposite.
Next, the researcher collects data from a sample and calculates the sample mean. Then, they use statistical techniques, such as t-tests or z-tests, to determine the probability of obtaining a sample mean as extreme as the one observed, assuming the null hypothesis is true. If this probability, known as the p-value, is less than a predetermined significance level (usually 0.05), the researcher rejects the null hypothesis in favor of the alternative hypothesis.
Applications
Single-sample hypothesis tests can be applied in various fields, such as psychology, biology, economics, and social sciences. For example, in psychology, researchers may use a single-sample hypothesis test to determine whether a treatment intervention has a significant effect on participants’ memory performance. In economics, a single-sample hypothesis test can be used to assess whether the average income of a certain group differs significantly from a specified value.
By conducting a single-sample hypothesis test, researchers can make evidence-based conclusions about the population under study and contribute to the advancement of knowledge in their respective fields.
Formulating the Null and Alternative Hypotheses
In hypothesis testing, the first step is to formulate the null and alternative hypotheses. The null hypothesis, denoted as H0, represents the default position or the assumption that there is no significant difference or effect. On the other hand, the alternative hypothesis, denoted as Ha or H1, represents the claim or assertion that contradicts the null hypothesis and suggests that there is a significant difference or effect.
When formulating the null and alternative hypotheses, it is essential to be specific and precise. The hypotheses should be based on the research question and the desired outcome of the study. The null hypothesis typically assumes that there is no relationship, no difference, or no effect, while the alternative hypothesis suggests the presence of a relationship, difference, or effect.
To illustrate, let’s consider an example. Suppose we are conducting a hypothesis test to determine if a new drug is effective in reducing blood pressure. The null hypothesis, in this case, would state that the drug has no effect on blood pressure, while the alternative hypothesis would assert that the drug does have an effect on blood pressure. Symbolically, the null hypothesis would be represented as H0: μ = μ0 (mean blood pressure is equal to a specific value), and the alternative hypothesis would be represented as Ha: μ ≠ μ0 (mean blood pressure is not equal to a specific value).
Examples of Null and Alternative Hypotheses:
- H0: There is no difference in test scores between students who receive tutoring and those who do not receive tutoring. Ha: There is a difference in test scores between students who receive tutoring and those who do not receive tutoring.
- H0: The new advertising campaign has no impact on sales. Ha: The new advertising campaign has a significant impact on sales.
- H0: The mean height of males and females is the same. Ha: The mean height of males and females is different.
- H0: There is no correlation between hours spent studying and exam scores. Ha: There is a positive correlation between hours spent studying and exam scores.
Formulating the null and alternative hypotheses correctly is crucial in hypothesis testing, as they guide the statistical analysis and the interpretation of the results. The hypotheses should be carefully constructed based on the research question and the desired outcome, ensuring that they are logical and testable.
Choosing a significance level
When conducting a hypothesis test for a single population, one of the important decisions that needs to be made is the choice of significance level. The significance level, denoted as α, determines how much evidence is required to reject the null hypothesis. It represents the probability of making a Type I error, which is the incorrect rejection of the null hypothesis when it is actually true.
Traditionally, a significance level of 0.05 (or 5%) has been used in many scientific studies. This means that if the p-value calculated from the data is less than 0.05, the null hypothesis is rejected. However, the choice of significance level is not arbitrary and should be carefully considered based on the context and goals of the study.
There are a few factors that can influence the choice of significance level. Firstly, the consequences of making a Type I error should be taken into account. If the consequences are severe, it may be appropriate to choose a lower significance level to minimize the chance of making an incorrect decision. On the other hand, if the consequences of a Type I error are not significant, a higher significance level may be acceptable.
Another factor to consider is the amount of available evidence or prior research on the topic. If there is strong prior evidence supporting the alternative hypothesis, a higher significance level may be justified. Conversely, if there is limited or conflicting evidence, a lower significance level may be more appropriate to be more conservative in drawing conclusions.
In summary, choosing a significance level involves balancing the risk of making a Type I error with the potential consequences and available evidence. It is an important decision that should be made thoughtfully and in consultation with domain experts. Ultimately, the significance level chosen should be justified and align with the goals and context of the study.
Selecting an appropriate test statistic

When conducting a hypothesis test for a single population mean or proportion, it is important to choose an appropriate test statistic that will help assess the evidence against the null hypothesis. The choice of test statistic depends on the nature of the data and the specific hypothesis being tested.
For a hypothesis test involving a population mean, the most commonly used test statistic is the z-score. This statistic is calculated by subtracting the hypothesized population mean from the sample mean, and dividing this difference by the standard deviation of the sample. The z-score measures how many standard deviations the sample mean is away from the population mean under the null hypothesis. It follows a standard normal distribution, which allows us to calculate probabilities and determine the significance of the result.
Alternatively, if the population standard deviation is unknown, the t-test statistic can be used. The t-test is similar to the z-test, but it uses the sample standard deviation instead of the population standard deviation. The t-test follows a t-distribution, which has thicker tails compared to the standard normal distribution. This accounts for the uncertainty introduced by estimating the population standard deviation from the sample.
For hypothesis tests involving a population proportion, the most common test statistic is the z-score. In this case, the test statistic is calculated by subtracting the hypothesized population proportion from the sample proportion, and dividing this difference by the standard error of the sample proportion. The z-score is then compared to the standard normal distribution to determine the significance of the result.
It is essential to choose the appropriate test statistic based on the type of data and the specific hypothesis being tested. By selecting the right test statistic, we can make accurate inferences about the population parameter of interest and draw meaningful conclusions.
Calculating the p-value
The p-value is a measure of the evidence against the null hypothesis in a hypothesis test. It tells us how likely we would observe the data, or more extreme data, assuming that the null hypothesis is true. The smaller the p-value, the stronger the evidence against the null hypothesis.
To calculate the p-value, we first determine the test statistic for the hypothesis test. The test statistic is a numerical value that summarizes the data and allows us to compare it to the null hypothesis. The choice of test statistic depends on the specific hypothesis test being conducted.
Once we have the test statistic, we use it to calculate the p-value. This involves determining the probability of observing a test statistic as extreme or more extreme than the one calculated, assuming that the null hypothesis is true. The calculation of the p-value depends on the distribution of the test statistic under the null hypothesis.
If the p-value is less than a pre-determined significance level (commonly 0.05), we reject the null hypothesis in favor of the alternative hypothesis. This means that the data provides strong evidence against the null hypothesis and supports the alternative hypothesis. If the p-value is greater than the significance level, we fail to reject the null hypothesis. This means that the data does not provide enough evidence to support the alternative hypothesis and we do not have strong enough evidence to reject the null hypothesis.
In conclusion, calculating the p-value is an important step in hypothesis testing. It allows us to quantify the evidence against the null hypothesis and make informed decisions about the validity of our hypothesis.
Interpreting the results
Once the hypothesis test for a single population parameter has been conducted, it is important to interpret the results properly. The interpretation will depend on the specific test statistic used and the corresponding p-value or confidence interval.
If the p-value is less than the chosen significance level (commonly 0.05), then there is evidence to reject the null hypothesis in favor of the alternative hypothesis. This means that the data provide enough evidence to support the claim being made about the parameter. On the other hand, if the p-value is greater than the significance level, then there is not enough evidence to reject the null hypothesis and the claim cannot be supported.
When interpreting the confidence interval, if the parameter being tested is within the interval, then there is not enough evidence to reject the null hypothesis. However, if the parameter is not within the interval, then there is evidence to suggest that the claim being made about the parameter is true.
It is important to remember that statistical significance does not necessarily imply practical significance. Even if a hypothesis test yields statistically significant results, the effect size and practical implications should also be considered. Additionally, it is always good practice to report the exact p-value rather than simply stating whether it is significant or not, as this provides more information about the strength of the evidence.