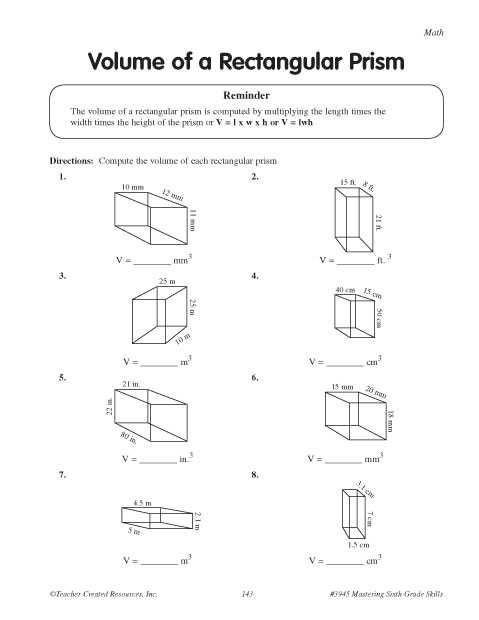
If you’re looking to reinforce your understanding of the surface area of a triangular prism, you’ve come to the right place. In this comprehensive worksheet, we provide you with a variety of exercises and step-by-step solutions to help you master this important mathematical concept. Whether you’re a student wanting to improve your skills or a teacher searching for resources to enrich your lessons, this worksheet is designed to meet your needs.
This worksheet is carefully structured to guide you through the process of calculating the surface area of a triangular prism, step-by-step. Each exercise presents you with a different triangular prism, asking you to find its surface area. You’ll need to identify the base and height of the triangular base, and then apply the appropriate formula to calculate the area of the base. Next, you’ll determine the lateral area of the prism by calculating the perimeter of the base and multiplying it by the height. Finally, you’ll add the base area and the lateral area to find the total surface area of the prism.
With each exercise, you’ll find detailed solutions, including all necessary calculations and explanations. This way, you can easily check your answers and understand the reasoning behind each step. Additionally, the worksheet includes extra practice problems at the end, so you can further strengthen your skills and deepen your understanding of the surface area of a triangular prism.
Surface Area of Triangular Prism Worksheet with Answers PDF
A triangular prism is a three-dimensional shape with two triangular bases and three rectangular faces. Calculating the surface area of a triangular prism is an important skill in geometry, as it allows us to determine the total area of all the faces of the prism. To practice and reinforce this skill, teachers often provide students with worksheets that contain a variety of problems involving triangular prisms and their surface areas.
These surface area of triangular prism worksheets with answers are typically in PDF format, making them easily accessible and printable. They usually include a set of problems that require students to find the surface area of different triangular prisms by calculating the area of each face and adding them together. The answers are provided, allowing students to check their work and understand their mistakes. Some worksheets may also include word problems or additional challenges to further enhance students’ problem-solving skills.
Using these worksheets, students can practice applying the formula for finding the surface area of a triangular prism, which is:
Surface Area = 2 * (Area of Base) + (Perimeter of Base) * (Height)
Here, the area of the base is calculated using the base’s length and height, while the perimeter of the base is calculated by adding the lengths of all the sides of the base.
By solving the problems provided in these worksheets, students can strengthen their understanding of the concept and develop their ability to calculate the surface area of a triangular prism accurately.
What is a Triangular Prism?
A triangular prism is a three-dimensional solid object that has two triangular bases and three rectangular faces.
The triangular bases of a prism are identical and parallel to each other. They are connected by three rectangular faces, which are perpendicular to the triangular bases.
The triangular prism gets its name from its shape – the two bases are triangles. These triangular bases can be equilateral (where all sides and angles are equal) or scalene (where the sides and angles can be different). The rectangular faces of the prism are typically oblong in shape.
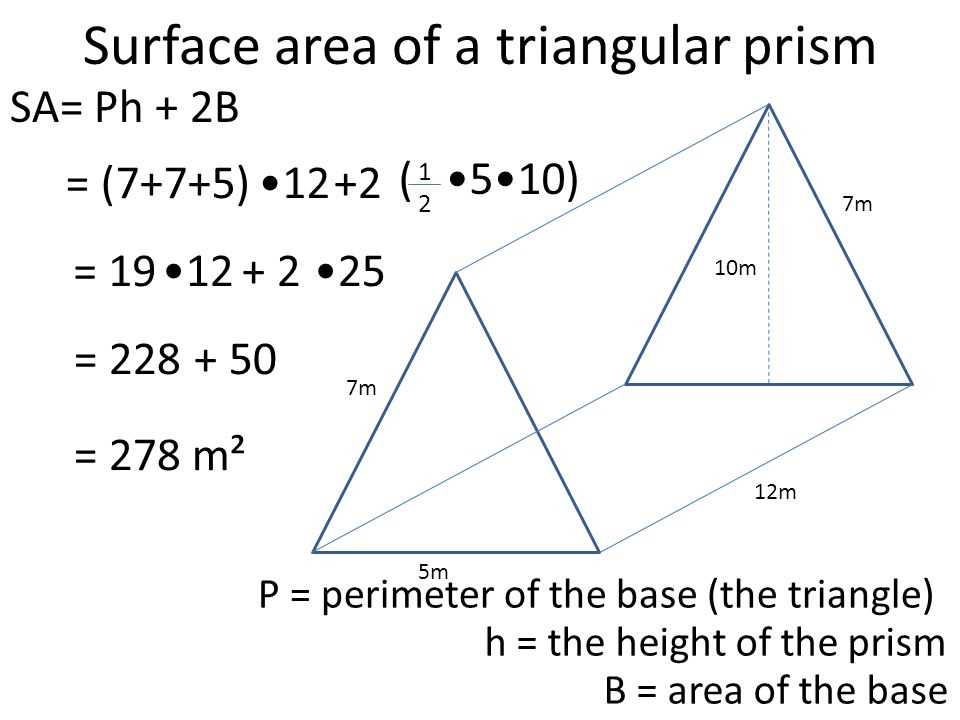
The total surface area of a triangular prism is calculated by finding the sum of the areas of its triangular bases and rectangular faces. It can be determined using the formula: SA = 2B + Ph, where B is the area of one triangular base, P is the perimeter of one triangular base, and h is the height of the prism.
Triangular prisms are commonly encountered in real-world objects such as buildings, packaging boxes, and triangular-based pyramids. Understanding the properties and calculations associated with triangular prisms helps in various mathematical and practical applications.
In conclusion, a triangular prism is a solid object with two identical triangular bases and three rectangular faces. Its surface area can be calculated using specific formulas, and its shape can be found in many everyday objects.
Understanding Surface Area
The surface area of an object refers to the total area of all its surfaces. In mathematical terms, it is the sum of the areas of all the faces of the object. Understanding surface area is important in various fields, such as architecture, engineering, and geometry.
To calculate the surface area of a triangular prism, for example, one must consider the area of each face and add them together. A triangular prism has two triangular faces and three rectangular faces. The formula to find the surface area of a triangular prism is (2 * base area of a triangular face) + (perimeter of the triangular base * height of the triangular prism) + (2 * area of a rectangular face).
- The base area of a triangular face can be calculated using the formula 1/2 * base * height of the triangular face.
- The perimeter of the triangular base is found by adding the lengths of all three sides of the triangle.
- The area of a rectangular face is calculated by multiplying the length and width of the rectangle.
By understanding the concept of surface area and the formulas used to calculate it, one can accurately determine the amount of material needed to cover an object’s surface or the amount of paint required to paint it. Additionally, understanding surface area can help in analyzing and creating 3D models and structures with precise measurements.
Formula for Finding the Surface Area of a Triangular Prism
A triangular prism is a three-dimensional shape that consists of two triangular bases and three rectangular faces. To find the surface area of a triangular prism, we need to calculate the combined area of these surfaces. The formula for finding the surface area of a triangular prism is:
Surface Area = Area of the Two Triangular Bases + Area of the Three Rectangular Faces
To calculate the area of the two triangular bases, we use the formula for the area of a triangle, which is:
Area of a Triangle = (1/2) × Base × Height
For a triangular prism, the base and height of each triangular base can be different, so you will need to calculate the area for each triangular base separately and then add them together.
To calculate the area of the three rectangular faces, we use the formula for the area of a rectangle, which is:
Area of a Rectangle = Length × Width
For a triangular prism, each rectangular face will have different dimensions, so you will need to calculate the area for each rectangular face separately and then add them together.
Once you have calculated the areas of the two triangular bases and the three rectangular faces, you can add them together to find the total surface area of the triangular prism.
Example Problems
In order to practice calculating the surface area of triangular prisms, let’s work through a couple of example problems. Remember, the formula to find the surface area of a triangular prism is:
Surface Area = 2(ab + bc + ac) + (2 × Area of the triangle base)
Example 1:
A triangular prism has a base with sides measuring 5 cm, 7 cm, and 8 cm. The height of the prism is 10 cm. Calculate the surface area.
Solution:
- First, calculate the area of the triangle base using Heron’s formula or another appropriate method. Let’s assume the area is 15 cm2.
- Next, calculate the values of ab, bc, and ac. For this example, ab = 5 × 7 = 35 cm2, bc = 7 × 8 = 56 cm2, and ac = 5 × 8 = 40 cm2.
- Using the values from the previous step, calculate 2(ab + bc + ac), which in this case is 2(35 + 56 + 40) = 262 cm2.
- Finally, use the formula to calculate the surface area by adding the area of the triangle base. The surface area is 2 × 262 cm2 + (2 × 15 cm2) = 554 cm2.
Example 2:
A triangular prism has a base with sides measuring 12 cm, 15 cm, and 18 cm. The height of the prism is 8 cm. Calculate the surface area.
Solution:
- First, calculate the area of the triangle base using the appropriate method. Let’s assume the area is 40 cm2.
- Next, calculate the values of ab, bc, and ac. For this example, ab = 12 × 15 = 180 cm2, bc = 15 × 18 = 270 cm2, and ac = 12 × 18 = 216 cm2.
- Using the values from the previous step, calculate 2(ab + bc + ac), which in this case is 2(180 + 270 + 216) = 1324 cm2.
- Finally, use the formula to calculate the surface area by adding the area of the triangle base. The surface area is 2 × 1324 cm2 + (2 × 40 cm2) = 2728 cm2.
By working through these example problems, you can become more comfortable with calculating the surface area of triangular prisms. Remember to understand the formula and apply the appropriate calculations for each problem.
The Importance of Worksheets
Worksheets play an important role in education as they provide a structured and organized way for students to practice and reinforce their learning. They are valuable tools that help students develop and master various skills, including problem-solving, critical thinking, and computation. Worksheets also promote independent learning, allowing students to work at their own pace and review concepts independently.
Practice and Reinforcement: Worksheets provide opportunities for students to practice and reinforce what they have learned in class. They allow students to apply their knowledge and skills to solve problems and complete exercises. By practicing various types of problems, students gain a deeper understanding of the concepts and build confidence in their abilities.
Structured Learning: Worksheets provide a structured format for learning, presenting information in a clear and organized manner. They break down complex concepts into smaller, manageable steps, making it easier for students to grasp new material. The structured nature of worksheets helps students stay focused and on track while working through exercises.
Independent Learning: Worksheets promote independent learning by allowing students to work on their own. They can be used as self-assessment tools, giving students the opportunity to identify areas where they need further practice or review. Worksheets also encourage students to take responsibility for their own learning and develop problem-solving skills.
Skills Development: Worksheets help students develop a range of skills, such as problem-solving, critical thinking, and computation. They provide opportunities for students to apply these skills in real-world scenarios, helping them to develop a deeper understanding of the subject matter. Worksheets can also be tailored to target specific skills or concepts, allowing students to focus on areas where they need additional practice or support.
Varied Learning Experiences: Worksheets can be designed to provide a variety of learning experiences, including visual, auditory, and kinesthetic. They can incorporate diagrams, charts, and graphs to enhance understanding and engagement. Worksheets can also include hands-on activities or interactive elements, making learning more interactive and enjoyable.
In conclusion, worksheets play a crucial role in education by providing students with structured practice, promoting independent learning, and developing a range of important skills. They offer a valuable resource for both teachers and students and have proven to be effective tools for enhancing learning outcomes.
Providing Answers for Practice

When it comes to learning and practicing math, having access to answers can be incredibly helpful. It allows students to check their work and identify areas where they may need additional practice. That’s why providing answers for practice exercises, such as those related to the surface area of a triangular prism, can be a valuable resource for both teachers and students.
By providing answers in a worksheet or PDF format, students can easily refer to the correct solution and compare it to their own. This not only helps them understand any mistakes they may have made, but it also reinforces the correct method and formula for calculating the surface area of a triangular prism. Additionally, having answers readily available encourages independent learning as students can work through the problems at their own pace.
In the provided worksheet or PDF, students will find a series of exercises that require them to calculate the surface area of various triangular prisms. Each exercise will have a corresponding answer, allowing students to self-assess their progress. Here is an example of how the answers may be presented:
| Exercise | Surface Area (cm²) |
|---|---|
| 1 | 72 |
| 2 | 90 |
| 3 | 64 |
| 4 | 108 |
With these answers, students can compare their own calculations to the provided solutions. If they do not match, they can revisit their work and attempt to identify any mistakes. This process of self-correction is instrumental in reinforcing learning and improving mathematical skills.
Overall, providing answers for practice exercises is a valuable tool in the learning process. It enhances understanding, promotes independent learning, and allows students to self-assess their progress. By utilizing worksheets or PDFs with answer keys, educators can support students in their mathematical journey and encourage them to strive for accuracy and mastery.