Synthetic division is a method used in algebra to divide polynomials with a simplified and straightforward approach. It is particularly useful in finding the roots of polynomial equations and simplifying polynomial expressions. To practice this method effectively, it is crucial to have a comprehensive worksheet with answers that can guide students through the process step by step.
A synthetic division worksheet with answers typically contains a series of polynomial division problems. Each problem presents a polynomial equation and requires students to divide it by a given factor. The worksheet provides step-by-step instructions on how to apply the synthetic division method to solve these problems. By following the given steps, students can practice the division process and determine the quotient and remainder for each equation.
Having a worksheet with answers is essential as it allows students to verify their solutions and understand where they made mistakes, if any. It provides immediate feedback and helps in identifying areas that need further clarification or practice. Additionally, the answers serve as a useful reference for students to compare their work and gauge their understanding of the synthetic division method.
Practicing synthetic division using a worksheet with answers can significantly improve students’ proficiency in this method. It helps build confidence, reinforce understanding, and enhance problem-solving skills. With regular practice, students can become proficient in dividing polynomials using synthetic division, enabling them to solve more complex polynomial equations with ease.
Synthetic Division Worksheet with Answers: Practice Division of Polynomials
Division of polynomials can be a challenging concept to grasp, but with enough practice, it becomes easier to understand and apply. One effective way to practice division of polynomials is by using a synthetic division worksheet with answers. These worksheets provide a structured and organized format for practicing synthetic division, allowing students to improve their skills and gain confidence in their abilities.
A synthetic division worksheet typically consists of several polynomial division problems, along with step-by-step instructions on how to perform synthetic division. The worksheet may also include an answer key, which allows students to check their work and identify any mistakes they may have made. This feedback is invaluable for learning and improving, as it helps students understand where they went wrong and how to correct their errors.
Working through a synthetic division worksheet with answers allows students to practice the division of polynomials in a systematic way. By following the instructions and applying the method of synthetic division, students can gain a deeper understanding of the concept and develop their problem-solving skills. With each problem they solve, they become more familiar with the process and more confident in their abilities.
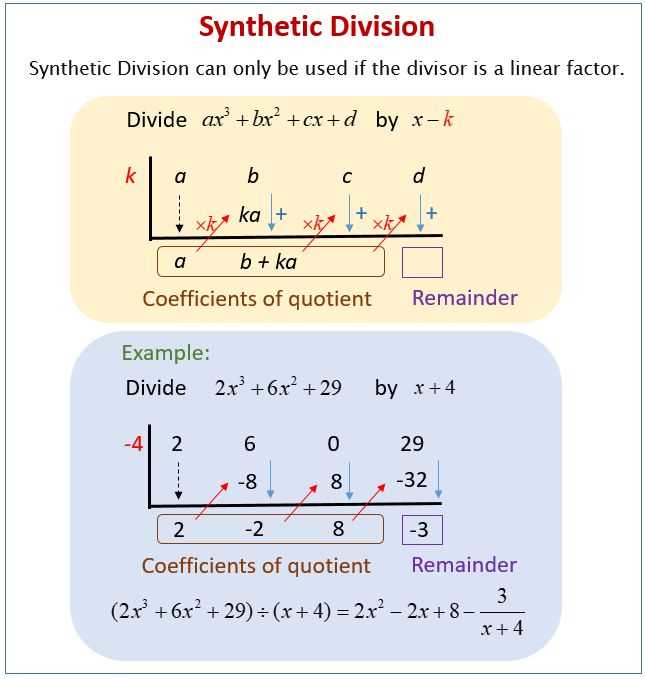
It is important to note that synthetic division is a specific method used for dividing polynomials with a linear divisor. It is often used when the divisor has the form (x – r), where r is a constant. By using synthetic division, the process is simplified, making it easier to perform the division and find the quotient and remainder.
In conclusion, using a synthetic division worksheet with answers is an effective way to practice division of polynomials. Through repeated practice and exposure to different problems, students can improve their understanding and mastery of this concept. The structured format of the worksheet, along with the provided answers, allows for self-assessment and self-correction, leading to better learning outcomes.
Understanding Synthetic Division:
Synthetic division is a method used to divide a polynomial by a binomial of the form (x-a). This method is particularly useful when the dividend is written in descending order and the divisor is a linear binomial. It provides a systematic way of dividing polynomials and can simplify calculations.
In synthetic division, the coefficients of the dividend are written in a horizontal row, with the terms arranged in decreasing powers of x. The divisor, in the form (x-a), is written in the first row, with the constant term “a” as a negative value. The division is performed by bringing down the first coefficient and multiplying it by “a”, then adding the result to the next coefficient. The process is repeated until all coefficients have been processed, resulting in a new row of coefficients.
Understanding synthetic division is important in algebra as it allows for the efficient division of polynomials, especially when finding the roots of an equation or simplifying complex expressions. It can also be used to evaluate polynomials at specific values of x, making it a valuable tool in solving problems in various fields of mathematics, science, and engineering.
Benefits of Synthetic Division:
Synthetic division is a powerful tool in algebra that allows us to divide polynomials quickly and efficiently. It offers several benefits over long division, making it a preferred method for simplifying algebraic expressions.
1. Fast and efficient: One of the main advantages of synthetic division is its speed. It enables us to divide polynomials in a fraction of the time it would take using traditional long division. This can be especially useful when dealing with complex or large polynomials, saving both time and effort.
2. Simplifies equations: Synthetic division helps simplify equations by reducing them to a lower degree. By dividing a higher-degree polynomial by a linear factor, we can obtain a simpler polynomial expression. This simplification allows us to solve equations more easily and analyze their properties more effectively.
3. Useful for finding zeroes: Synthetic division is commonly used to find the zeroes of a polynomial. By dividing the polynomial by a linear factor, we can identify any roots or zeros of the polynomial. This information is crucial in many applications, such as finding the x-intercepts of a graph or solving real-life problems.
4. Can be used for polynomial factorization: Synthetic division is an important step in factoring polynomials. By dividing a polynomial by a linear factor and obtaining a remainder of zero, we can conclude that the linear factor is a factor of the original polynomial. This allows us to further simplify the polynomial expression and determine its complete factorization.
Overall, synthetic division is a valuable tool in algebra that offers numerous benefits. Its speed, simplification capabilities, and usefulness in finding zeroes and factoring polynomials make it an essential technique for solving algebraic problems effectively.
Key Terms in Synthetic Division:
Dividend refers to the polynomial being divided in synthetic division. It is the polynomial that is being divided by the binomial divisor.
Divisor is the binomial of the form x – c that is used to divide the polynomial in synthetic division.
Quotient is the result of the synthetic division. It is the polynomial that represents the actual division of the dividend by the divisor. The quotient is obtained by using the coefficients obtained during the synthetic division process.
Remainder is the polynomial of degree less than the divisor that represents the remainder of the division. If the remainder is zero, it means that the divisor is a factor of the dividend.
Root or solution refers to the values of x that make the polynomial equal to zero. In synthetic division, if the remainder is zero, it means that the divisor is a factor of the polynomial and the value of x – c is a root/solution.
Synthetic Division Table is a table used to perform synthetic division. It includes the coefficients of the dividend and the constant c, as well as the steps for the synthetic division process.
How to Perform Synthetic Division:
Synthetic division is a method used to divide polynomials. It allows you to divide a polynomial by a linear factor to find the quotient and remainder. This method is particularly helpful when you need to factor a polynomial or solve equations involving polynomials.
To perform synthetic division, follow these steps:
- Write the polynomial in descending order of its exponents. For example, if the polynomial is 3x^3 – 2x^2 + 5x – 1, write it as 3x^3 – 2x^2 + 5x – 1.
- Identify the divisor, which should be in the form of (x – a) where a is a constant. For example, if the divisor is (x – 2), write it as (x – 2).
- Set up a synthetic division table. Write the coefficients of the polynomial in the top row and the divisor in the second row. Leave enough space in the table to perform the synthetic division.
- Bring down the first coefficient from the top row into the empty space in the third row of the table.
- Multiply the divisor by the number in the third row and write the result below the second row.
- Add the numbers in the second and third rows and write the result in the fourth row.
- Repeat steps 4-6 until you have gone through all the coefficients of the polynomial.
- The number in the final row represents the quotient, while the number in the last cell of the fourth row represents the remainder.
By following these steps, you can easily perform synthetic division to divide polynomials and find the quotient and remainder. Practice using synthetic division on different polynomials to become more proficient in this method.
Examples of Synthetic Division:
The synthetic division method is a process that allows us to divide a polynomial by a linear factor. This method is particularly useful when we are trying to find the zeros or roots of a polynomial. Here are a few examples to illustrate how synthetic division is applied.
Example 1: Division by x – 3
Suppose we have the polynomial P(x) = 2x^3 – 5x^2 + 3x – 6 and we want to divide it by the linear factor x – 3. We can use synthetic division to perform the division:
| 3 | | | 2 | -5 | 3 | -6 |
| | | 6 | 3 | 18 | ||
| | | 2 | 1 | 6 | 12 |
The result of the synthetic division is the polynomial Q(x) = 2x^2 + x + 6. Therefore, when we divide P(x) by x – 3, the quotient is Q(x) = 2x^2 + x + 6.
Example 2: Division by x + 2
Let’s consider another example where we want to divide the polynomial P(x) = 3x^4 + 2x^3 – 5x^2 + x + 4 by the linear factor x + 2:
| -2 | | | 3 | 2 | -5 | 1 | 4 |
| | | -6 | 8 | -6 | 10 | ||
| | | 3 | -4 | 3 | -5 | 14 | |
| | | 3 | -1 | -1 | -6 | 8 |
The result of the synthetic division is the polynomial Q(x) = 3x^3 – x^2 – x – 6. Therefore, when we divide P(x) by x + 2, the quotient is Q(x) = 3x^3 – x^2 – x – 6.
These examples demonstrate how synthetic division can be used to divide polynomials by linear factors. By applying this method, we can easily find the quotient and accurately solve polynomial equations.
Tips and Tricks for Synthetic Division:
In order to successfully perform synthetic division, it is important to understand the steps involved and to practice regularly. Here are some tips and tricks that can help make the process easier:
1. Familiarize yourself with the format:

Take the time to understand the correct format for synthetic division. The dividend should be written in descending powers of the variable, and the divisor should be written as a binomial, with only the variable and its coefficient. This will help ensure that you divide the terms correctly.
2. Keep track of the signs:

Pay attention to the signs in the problem. When you bring down the first term in each step, make sure to include the sign. This will help ensure that you perform the addition and subtraction correctly.
3. Start with the highest power:
When performing synthetic division, it is easiest to start with the highest power of the variable and work your way down. This will help keep the process organized and prevent mistakes.
4. Don’t forget to write the final answer:
After completing the synthetic division, write the final answer in the form of a quotient and a remainder. The quotient represents the polynomial after division, and the remainder represents what is left over.
By following these tips and tricks, you can improve your skills in synthetic division and make the process easier and more efficient.
Common Mistakes to Avoid in Synthetic Division:
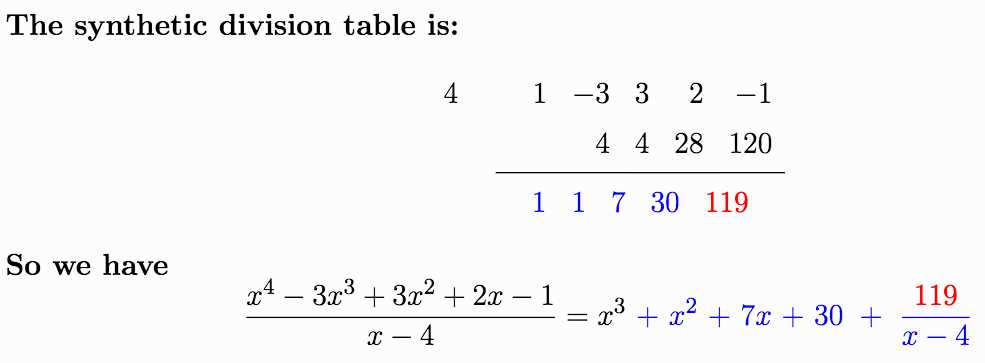
When working with synthetic division, it is important to be aware of common mistakes that can occur. By identifying these mistakes, you can avoid them and ensure accurate results in your calculations. Here are some of the most common mistakes to watch out for:
1. Incorrectly identifying the divisor:
One common mistake is using the wrong factor as the divisor in synthetic division. It is important to carefully determine the correct factor to divide by. Double-check the equation or problem to ensure you are using the correct divisor.
2. Misplacing the coefficients:
Another error that can occur is misplacing the coefficients when setting up the synthetic division. Make sure to align the coefficients properly in the dividend, ensuring each coefficient is in the correct place. This will help you accurately perform the synthetic division.
3. miscalculating the signs:
Sign errors are another common mistake to be aware of. When combining the terms and performing calculations, it is important to pay attention to the signs. Adding or subtracting inappropriately can lead to incorrect results.
4. Neglecting to consider remainders:
Do not forget to consider remainders when interpreting the results of synthetic division. Be sure to include the remainder (if any) when expressing the final answer. Neglecting to consider remainders can result in an incomplete or inaccurate solution.
In conclusion, by being mindful of these common mistakes, you can avoid errors and achieve accurate results when using synthetic division. Being aware of these pitfalls will help you to effectively solve problems and gain a better understanding of the concept. Regular practice and careful attention to detail will lead to success in synthetic division.