
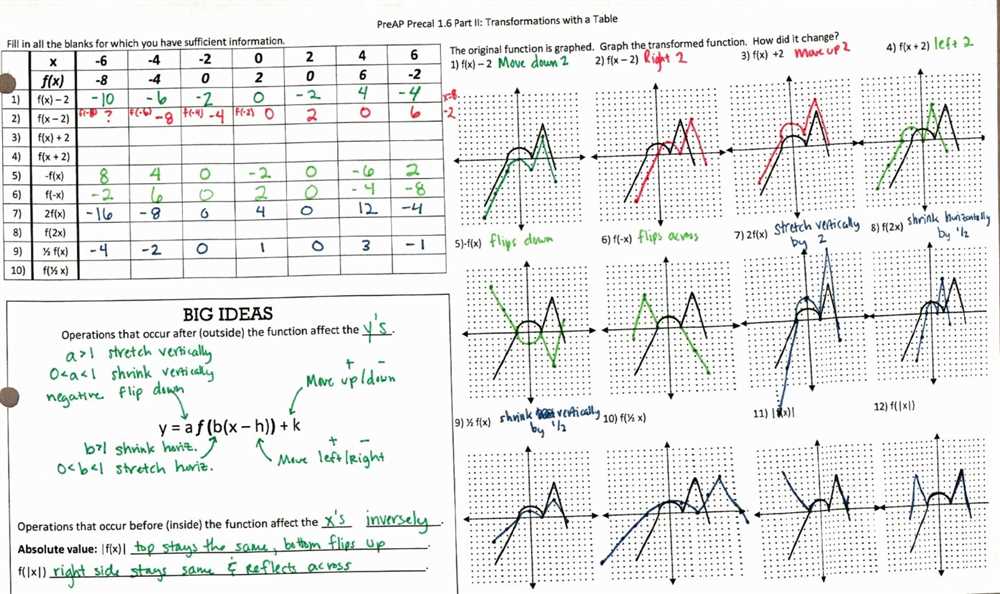
Understanding the concept of transformation is a fundamental skill in geometry. By learning how shapes can be transformed through translation, rotation, and reflection, we can better understand their properties and relationships with one another.
Transformation is the process of changing the position, orientation, or size of a shape while preserving its properties. Each type of transformation has its own unique characteristics and rules, and it is important to understand how they can affect a shape.
Translation is the simplest type of transformation, where a shape is moved without changing its size or orientation. The shape is simply shifted in a certain direction, either horizontally or vertically, by a certain distance. This can be visualized as sliding the shape along a given path.
Rotation, on the other hand, involves turning a shape around a fixed point called the center of rotation. The shape is rotated by a certain angle, either clockwise or counterclockwise. This can be imagined as spinning the shape around a pivot point.
Lastly, reflection is a transformation that flips a shape over a line called the line of reflection. The shape is essentially mirrored across this line, creating a symmetrical result. Reflection can be thought of as folding the shape in half along the line of reflection.
By understanding these fundamental transformations and practicing applying them to different shapes, we can develop a deeper understanding of geometry and further enhance our problem-solving skills. Unlocking the answer key to these shape transformations opens up a world of possibilities and challenges in the field of mathematics!
Transformation of Shapes Answer Key
In the study of geometry, one important concept is the transformation of shapes. This involves changing the position, orientation, or size of a shape without altering its basic properties. Understanding how shapes can be transformed is essential for various applications, such as computer graphics, architecture, and engineering.
When working with transformations, it is crucial to have a clear understanding of the key terms and concepts that are involved. For instance, translation refers to moving a shape horizontally or vertically without changing its size or shape. Rotation involves spinning a shape around a fixed point, while reflection involves flipping a shape over a line. Lastly, scaling refers to changing the size of a shape uniformly.
A key component of successfully performing transformations is understanding the coordinate system. Each point on a shape is represented by a pair of coordinates (x, y), where the x-coordinate represents the horizontal position and the y-coordinate represents the vertical position. By applying different mathematical operations to these coordinates, we can achieve the desired transformation.
Using an answer key for transformation exercises can be incredibly helpful for checking the correctness of your work. It allows you to compare your results with the correct transformations and identify any mistakes you may have made. By studying the answer key, you can also gain a better understanding of the steps involved in each transformation and improve your overall knowledge of geometry.
The Transformation Process
- Translation: To perform a translation, you need to determine the distance and direction of the movement. This is done by adding or subtracting the same value from the x and y coordinates of each point.
- Rotation: To rotate a shape, you need to determine the angle of rotation and the center of rotation. The new coordinates of each point can be found using trigonometric functions and matrix multiplication.
- Reflection: Reflecting a shape involves changing the sign of either the x or y coordinates, depending on the line of reflection. If the line is vertical, the x coordinates remain the same, but the y coordinates change sign. If the line is horizontal, the y coordinates remain the same, but the x coordinates change sign.
- Scaling: Scaling a shape involves multiplying the x and y coordinates of each point by a scaling factor. The scaling factor determines whether the shape becomes larger or smaller.
By understanding the key concepts and steps involved in transforming shapes, and by using answer keys to check your work, you can gain a strong foundation in geometry and enhance your problem-solving skills.
Understanding Shapes and Transformations
In mathematics, shapes play a fundamental role in understanding the world around us. Whether they are two-dimensional or three-dimensional, shapes can be found everywhere in nature and human-made objects. By studying shapes, we can gain insights into their properties, relationships, and transformations.
Shapes come in various forms, such as circles, squares, triangles, and rectangles. Each shape has its own unique characteristics, including the number of sides, angles, and lengths of its edges. These properties define the shape and allow us to identify and classify them.
Transformations refer to the changes that shapes undergo when they are modified in some way. These modifications can include translations, rotations, reflections, or dilations. Transformations help us understand how shapes can be moved, rotated, or flipped without changing their essential properties. By studying transformations, we can explore the relationships between different shapes and their altered versions.
When studying transformations, it is important to understand the concept of a coordinate system. A coordinate system provides a way to locate points in a plane using a pair of numbers called coordinates. By applying transformations, we can change the position and orientation of shapes on a coordinate plane.
In summary, understanding shapes and their transformations is essential in mathematics as it allows us to analyze and manipulate geometric objects in various contexts. Whether we are studying the properties of a specific shape or exploring how shapes change through transformations, these concepts provide a foundation for further mathematical exploration.
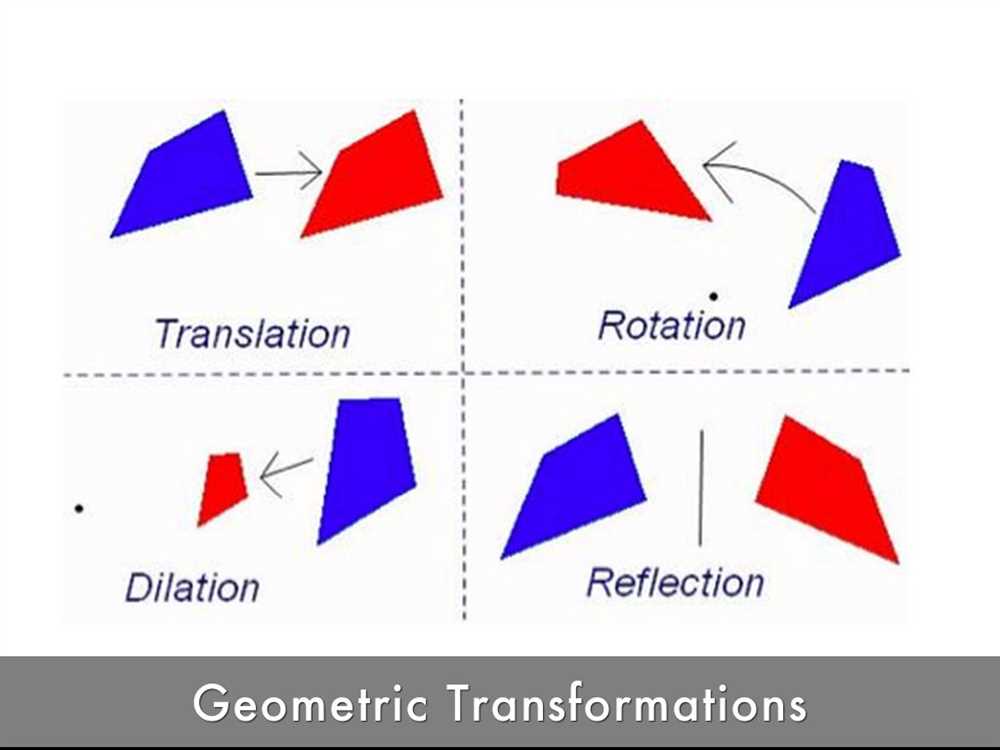
Types of Shape Transformations
Shape transformations are an important concept in mathematics and geometry. These transformations involve changing the position, size, or shape of a given shape. There are several types of shape transformations, including translation, reflection, rotation, and dilation. Each type of transformation has its own characteristics and properties.
1. Translation
Translation involves sliding a shape from one position to another, without changing its size or shape. This can be done by shifting the shape horizontally or vertically. In a translation, all points of the shape move the same distance and in the same direction.
2. Reflection
Reflection is a transformation that involves flipping a shape over a line, called the axis of reflection. The resulting shape is a mirror image of the original shape. The axis of reflection can be a vertical line, a horizontal line, or even a diagonal line.
3. Rotation

Rotation is a transformation that involves turning a shape around a fixed point, called the center of rotation. The shape rotates in a circular motion, creating new positions for its points. The center of rotation can be inside the shape, outside the shape, or even on the shape itself.
4. Dilation
Dilation is a transformation that involves changing the size of a shape, while keeping its shape and proportions intact. The shape can be enlarged or reduced in size. Dilation is performed by multiplying the coordinates of the shape’s points by a scale factor. This scale factor determines the degree of enlargement or reduction.
Understanding the different types of shape transformations is essential in solving problems involving geometric shapes. These transformations help us visualize and manipulate shapes, allowing us to analyze their properties, relationships, and patterns.
Translation
In mathematics, translation is a transformation that slides a figure in a specific direction without changing its shape or size. It is one of the basic transformations along with reflection, rotation, and dilation.
Translation involves moving every point of a figure a certain distance in a specific direction. This distance is called the vector of the translation. The vector is usually described using coordinates (x, y), where x represents the horizontal shift and y represents the vertical shift.
To perform a translation, you can think of the figure as being moved by a certain number of units to the left, right, up, or down. For example, if a figure is translated 3 units to the right and 2 units up, you would add 3 to each x-coordinate and 2 to each y-coordinate of the original figure to get the new coordinates.
A translation can also be represented using a translation matrix. The matrix is a 2×2 array that represents the horizontal and vertical shifts. For a translation (x, y), the translation matrix is:
| x | y |
| 1 | 0 |
| 0 | 1 |
When performing a translation, you can apply the translation matrix to each point of the figure to obtain the new coordinates. This method is often used when dealing with multiple points or complex figures.
Translations are commonly used in various fields, such as computer graphics, geometry, and physics. They are used to describe the movement of objects, the position of points, and many other applications. Understanding translations is crucial in order to work with shapes and figures effectively.
Rotation
In geometry, rotation is a transformation that turns a figure around a fixed point called the center of rotation. The figure is rotated by a certain angle in a specific direction.
To describe a rotation, we need to specify the center of rotation, the angle of rotation, and the direction of rotation. The center of rotation can be any point in the plane, and it remains fixed while the rest of the figure moves around it. The angle of rotation is measured in degrees or radians, and it determines how much the figure is turned. The direction of rotation can be clockwise or counterclockwise.
When a figure is rotated, each point of the figure moves in a circular path around the center of rotation. The distance from each point to the center of rotation remains the same before and after the rotation, which means that the shape and size of the figure are preserved.
In mathematics, rotation is often represented using matrices or complex numbers. Using matrix multiplication, we can apply a rotation transformation to a figure by multiplying its coordinates by a rotation matrix. The rotation matrix depends on the angle of rotation and the direction of rotation. Similarly, we can represent rotations using complex numbers, where the angle of rotation corresponds to the argument of the complex number and the direction of rotation can be determined by the sign of the angle.
Rotations have many applications in real life, such as in computer graphics, robotics, and physics. They are used to simulate movement and transformations in virtual environments, control the motion of robotic arms, and describe the behavior of rotating objects like planets or spinning tops.
Reflection
A reflection is a transformation that flips a figure over a line to create a mirror image. The line over which the figure is reflected is called the line of reflection. When a figure is reflected, its size and shape do not change, but its orientation is reversed. Reflections are often represented using dashed lines or arrows to indicate the line of reflection and the direction of the reflection.
To perform a reflection, you can imagine placing a mirror along the line of reflection and then seeing the image reflected in the mirror. Any point on the original figure will have a corresponding point on the reflected figure that is the same distance from the line of reflection, but on the opposite side.
For example:
- If the line of reflection is vertical, a point that is 3 units to the left of the line will be reflected to a point that is 3 units to the right of the line.
- If the line of reflection is horizontal, a point that is 5 units below the line will be reflected to a point that is 5 units above the line.
Reflections can be used to create symmetrical patterns and designs, as well as to solve geometric problems. By understanding reflections, you can analyze and describe the properties and relationships of shapes more effectively.
Dilations
A dilation is a transformation that alters the size of a shape without changing its shape. It involves stretching or shrinking the shape in relation to a fixed point called the center of dilation. The scale factor determines the amount of stretching or shrinking.
When performing a dilation, each point of the original shape is multiplied by the scale factor to determine its new coordinates. If the scale factor is greater than 1, the shape is stretched; if it is between 0 and 1, the shape is shrunk.
Example:
Suppose we have a triangle with vertices at (2, 3), (4, 5), and (6, 1). If we dilate the triangle with a scale factor of 2 and the center of dilation at the origin (0, 0), each of the vertices will be multiplied by the scale factor, resulting in the following new coordinates: (4, 6), (8, 10), and (12, 2).
A dilation can also be represented by a ratio, where the numerator represents the change in size in the x-direction and the denominator represents the change in size in the y-direction. For example, a dilation with a scale factor of 2 in the x-direction and 3 in the y-direction would be represented by the ratio 2:3.
Dilations are commonly used in various fields, such as computer graphics, mathematics, and cartography, to enlarge or reduce objects while maintaining their proportional similarity.
Applying Transformations
Transformations are fundamental operations in geometry that can change the shape, size, and position of objects. By applying different transformations, we can explore the relationships between different geometric figures and understand how they can be manipulated.
Translation: A translation is a transformation that shifts an object from one position to another without changing its size, shape, or orientation. It can be thought of as sliding the object along a straight line. To perform a translation, we need to know the distance and direction of the shift. For example, we can translate a triangle 2 units to the right and 3 units up by moving each vertex of the triangle accordingly.
Reflection: A reflection is a transformation that flips an object across a line, called the line of reflection. It creates a mirror image of the original object. The line of reflection acts as an axis of symmetry, dividing the object into two congruent halves. For example, we can reflect a square across a vertical line to create its mirror image.
Rotation: A rotation is a transformation that turns an object around a fixed point, called the center of rotation. It preserves the shape and size of the object but changes its orientation. For example, we can rotate a rectangle 90 degrees clockwise around its center to obtain a new position.
Dilation: A dilation is a transformation that changes the size of an object. It can either enlarge or reduce the size of the object while keeping its shape intact. A dilation is characterized by a scale factor, which determines the amount of enlargement or reduction. For example, we can dilate a triangle by a scale factor of 2 to make it twice as large as the original.
By understanding and applying these different transformations, we can analyze and manipulate geometric figures to solve problems and discover new insights in mathematics and geometry.