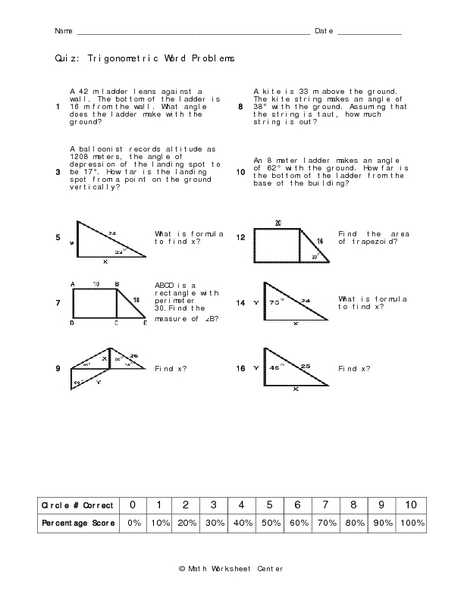
Trigonometry, the branch of mathematics that deals with the relationships between the angles and sides of triangles, is a fundamental concept in various fields, including engineering, physics, and architecture. To master trigonometry, students must tackle word problems that require them to apply their knowledge of triangles and trigonometric functions to solve real-life challenges.
When it comes to practicing trigonometry word problems, a trig word problems worksheet provides an essential tool for both teachers and students. This worksheet not only tests students’ understanding of trigonometric concepts but also helps them develop problem-solving skills.
In order to effectively solve trigonometry word problems, students must be able to identify the given information, determine which trigonometric formula or function to use, and set up the equation to find the unknown value. The trig word problems worksheet answer key provides students with the correct solutions, allowing them to check their work and understand the steps needed to arrive at the answer.
By working through a trig word problems worksheet and using the answer key to verify their solutions, students can build confidence in their trigonometry abilities and gain a deeper understanding of how trigonometry applies to real-life scenarios. This active learning approach not only enhances their mathematical skills but also prepares them to face complex problem-solving challenges in the future.
Understanding the basic trigonometric functions
Trigonometry is a branch of mathematics that deals with the relationships and properties of triangles. It is based on the concept of ratios and angles. The basic trigonometric functions, sine, cosine, and tangent, are essential tools used to solve problems involving angles and distances. These functions represent the ratios of the sides of a right triangle and provide valuable information about the angles and lengths within the triangle.
The sine function (sin) relates the length of the side opposite an angle to the hypotenuse of a right triangle. It can be used to find unknown side lengths or determine the measure of an angle. The cosine function (cos) relates the length of the side adjacent to an angle to the hypotenuse. It is also useful for finding unknown side lengths or angles. The tangent function (tan) relates the sine and cosine functions and helps to find the slope or incline of a line.
By using the values of these trigonometric functions and applying them to various problems, we can calculate distances, heights, angles, and other measurements. For example, in navigation, trigonometry is used to determine the position and distance between two points. In physics, it is used to analyze the motion and forces in objects. In engineering, trigonometry is applied to design structures and evaluate their stability.
Understanding the basic trigonometric functions is crucial for solving trigonometry problems and applying them to real-life situations. It allows us to find precise solutions and make accurate calculations. By mastering these functions, we can navigate complex mathematical problems and gain a deeper understanding of the world around us.
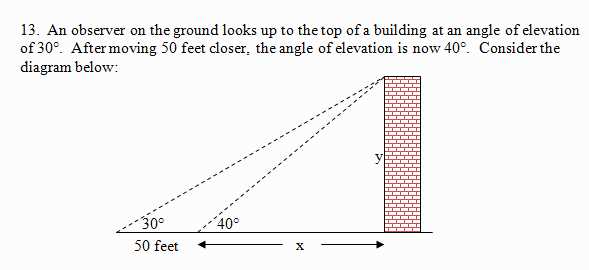
Solving right triangle trigonometry word problems
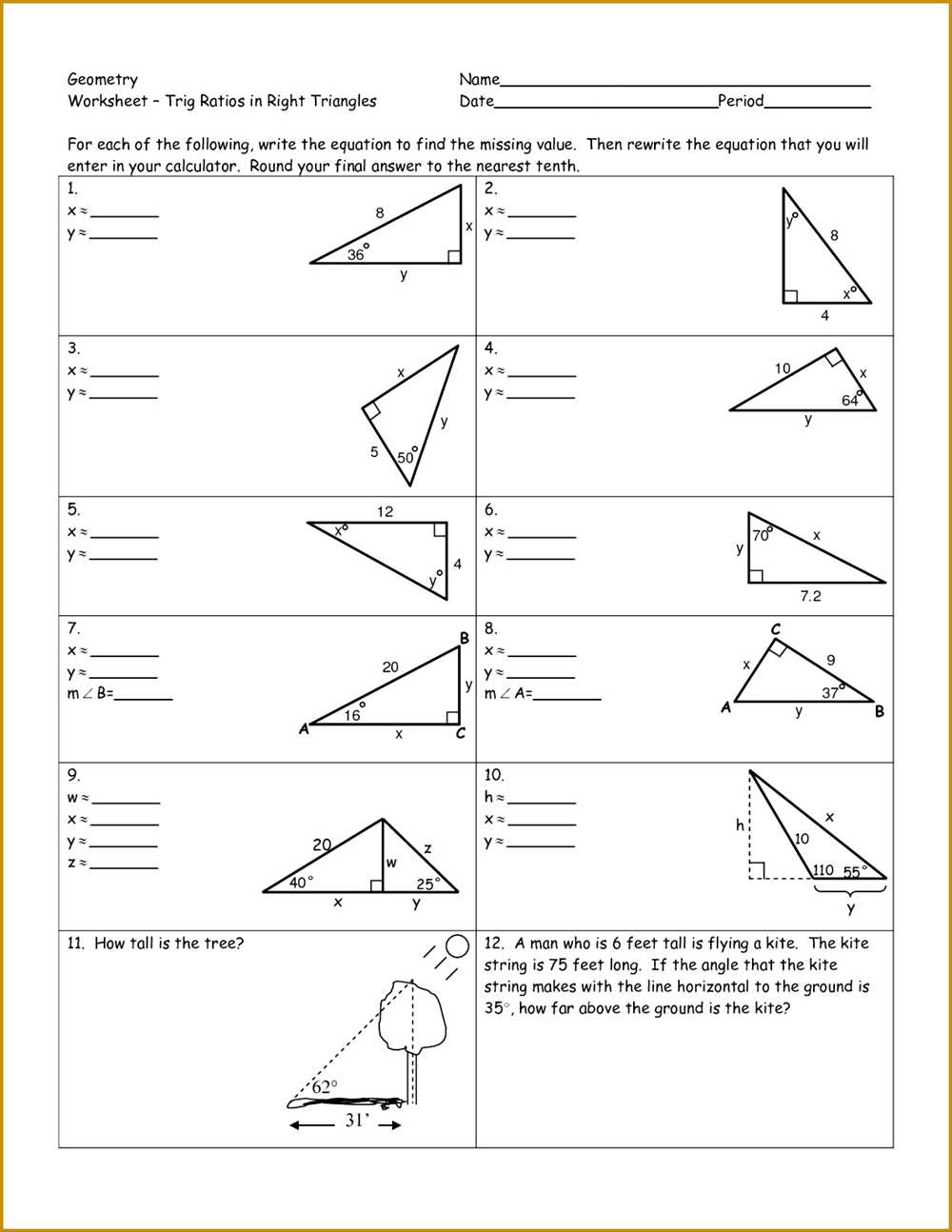
Right triangle trigonometry word problems involve using the properties of right triangles and trigonometric ratios to solve real-world scenarios. These problems often require the use of the sine, cosine, or tangent functions to find missing lengths or angles in a right triangle.
One common type of problem involves finding the length of one side of a triangle when the lengths of the other two sides are known. For example, given a right triangle with a known hypotenuse and one leg, you can use the Pythagorean theorem to find the length of the other leg. From there, you can use the appropriate trigonometric ratio to find any missing angles.
Another type of problem involves finding the measure of an angle in a triangle when the lengths of the sides are known. In these cases, you can use the inverse trigonometric functions (arcsin, arccos, or arctan) to find the angle. Once you have the measure of one angle, you can use the sum of angles in a triangle (180 degrees) to find the other angles.
It is important to carefully read the word problem and identify what information is given and what is being asked for. Drawing a diagram can also be helpful in visualizing the problem and identifying how the different angles and sides relate to each other.
In summary, solving right triangle trigonometry word problems involves applying the properties of right triangles and trigonometric ratios to find missing lengths and angles. It requires careful reading, diagramming, and the use of trigonometric functions and inverse trigonometric functions.
Using the unit circle to solve trigonometric equations
The unit circle is a helpful tool in solving trigonometric equations as it allows us to visualize the relationship between angles and coordinates on the circle. By understanding the unit circle and its properties, we can easily determine the values of sine, cosine, and tangent for various angles.
When solving trigonometric equations using the unit circle, we start by identifying the given angle and its reference angle. The reference angle is the acute angle formed between the terminal side of the given angle and the x-axis. By finding the reference angle, we can simplify the problem and focus on finding the correct quadrant on the unit circle.
Next, we use the properties of the unit circle to determine the values of sine, cosine, and tangent for the reference angle. These values can then be used to find the corresponding values for the given angle by considering the signs of the trigonometric functions in each quadrant.
To solve trigonometric equations, we must also consider any additional restrictions or conditions specified in the problem. For example, if the problem only asks for solutions within a certain range or interval, we must adjust our answers accordingly.
Overall, the unit circle is a powerful tool that allows us to solve trigonometric equations by visualizing the relationship between angles and coordinates on the circle. By understanding the properties of the unit circle and applying them to specific problems, we can accurately determine the values of sine, cosine, and tangent for any given angle.
Application of Trigonometry in Real-Life Scenarios

Trigonometry, a branch of mathematics that deals with the relationships between the angles and sides of triangles, has numerous applications in real-life scenarios. It is widely used in fields such as engineering, architecture, physics, navigation, and astronomy. By understanding and applying trigonometric principles, professionals can solve complex problems and make accurate calculations in a variety of practical situations.
One common application of trigonometry is in the design and construction of structures. Architects and engineers use trigonometric calculations to determine the angles and lengths of roof trusses, the heights and stability of buildings, and the dimensions of bridges and roadways. By applying trigonometric concepts such as the sine, cosine, and tangent functions, they can ensure that structures are built to withstand external forces and maintain their structural integrity.
In navigation and astronomy, trigonometry plays a critical role in determining distances and angles between celestial bodies and Earth. Astronomers use trigonometric principles to measure the distances to stars and galaxies, and to calculate the angles at which planets and other celestial objects appear in the sky. Navigators, both on land and at sea, rely on trigonometry to calculate their position and course using instruments such as compasses and sextants.
Furthermore, trigonometry is also used in surveying and mapping. Surveyors use trigonometric formulas to measure distances and angles, determine the elevation of land, and create accurate maps. By measuring the angles formed by landmarks and using trigonometric functions, surveyors can calculate the distances between points and create precise representations of the land.
In conclusion, trigonometry plays a vital role in various real-life scenarios, from the design and construction of structures to navigation, astronomy, and surveying. By applying trigonometric principles and formulas, professionals in these fields can solve complex problems and make accurate calculations that are crucial for their work.
Advanced trigonometric functions and identities
In trigonometry, advanced functions and identities go beyond the basic trigonometric relationships of sine, cosine, and tangent. These advanced functions involve combinations of trigonometric ratios and can be used to solve more complex problems in mathematics and physics. Understanding these functions is essential for tackling higher-level trigonometry problems.
One of the advanced trigonometric functions is the cosecant (csc) function, which is the reciprocal of the sine function. It is defined as csc(x) = 1/sin(x). The cosecant function is useful for finding the lengths of sides in right triangles or determining the amplitudes and periods of periodic functions.
Another important function is the secant (sec) function, which is the reciprocal of the cosine function. It is defined as sec(x) = 1/cos(x). The secant function is helpful in finding the lengths of sides in right triangles or determining the amplitudes and periods of periodic functions, similar to the cosecant function.
The cotangent (cot) function is the reciprocal of the tangent function and is defined as cot(x) = 1/tan(x). It is used to find the lengths of sides in right triangles or determine the slopes of curves and lines in calculus.
In addition to these advanced functions, there are various trigonometric identities that relate the different trigonometric ratios to each other. These identities can be used to simplify and solve trigonometric equations, such as the Pythagorean identities (sin^2(x) + cos^2(x) = 1) and the angle sum and difference identities (sin(A ± B) = sin(A)cos(B) ± cos(A)sin(B)). These identities are essential for manipulating trigonometric expressions and solving complex trigonometric equations.
Overall, understanding and applying advanced trigonometric functions and identities is crucial for solving more challenging trigonometry problems and for furthering mathematical and scientific knowledge.
Solving Trigonometric Equations Using Inverse Trigonometric Functions

Trigonometric equations involve the use of trigonometric functions such as sine, cosine, and tangent. Solving these equations often requires finding the values of the angles that satisfy the equation. The inverse trigonometric functions, also known as arc functions, are essential tools for solving such equations.
The inverse trigonometric functions, denoted as sin^-1, cos^-1, and tan^-1, allow us to find the angle that corresponds to a specific value of a trigonometric function. For example, if we have an equation sin(x) = 0.5, we can use the inverse sine function or sin^-1(0.5) to find the angle x that satisfies the equation. The inverse trigonometric functions take the output of a trigonometric function as input and provide the angle that produces that output.
To solve trigonometric equations using inverse trigonometric functions, we follow these steps:
- Identify the trigonometric equation and determine which inverse trigonometric function to use based on the given trigonometric function.
- Apply the inverse trigonometric function to both sides of the equation to isolate the angle.
- Use the properties of trigonometric functions and algebraic manipulation to simplify and solve for the angle.
- Check the solution by substituting the value of the angle back into the original equation to ensure it satisfies the equation.
By using inverse trigonometric functions, we can effectively solve trigonometric equations and find the angles that satisfy them. These equations often arise in practical applications, such as finding distances or angles in geometry, physics, and engineering. Understanding how to apply inverse trigonometric functions is essential for solving these types of problems accurately.