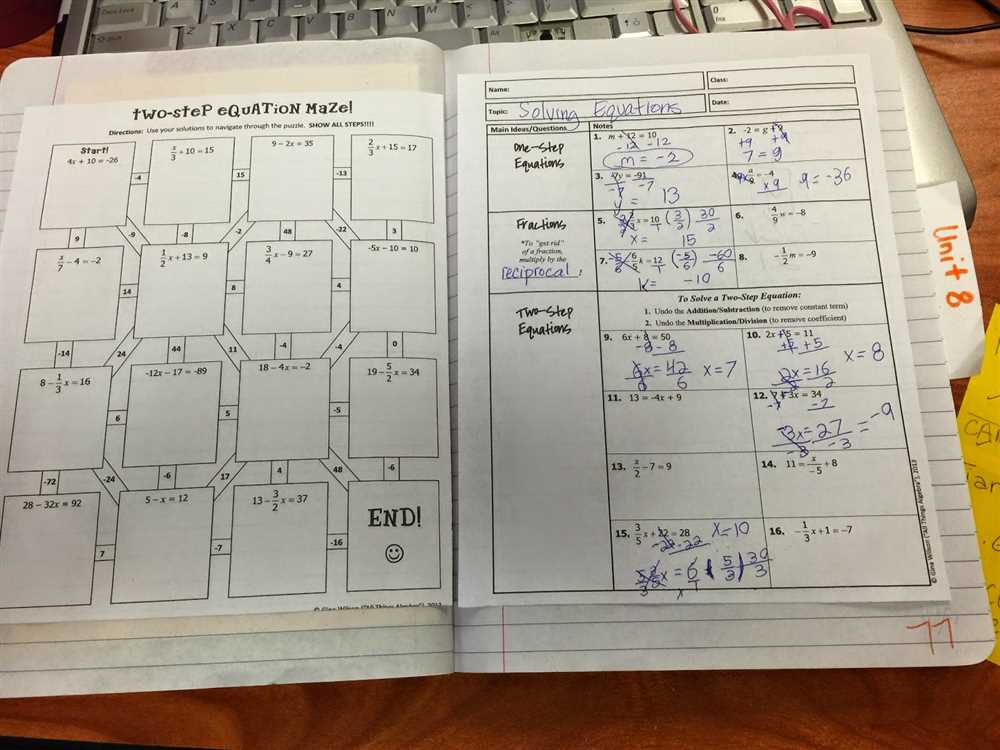
In mathematics, solving equations is a fundamental skill that students need to master. However, the process of solving equations can sometimes be challenging and tedious. To make this process more engaging and enjoyable, educators have developed various creative methods. The two-step equation maze is one such method.
A two-step equation maze is a puzzle that requires students to solve a series of equations to navigate through a maze and find the correct path to the exit. Each equation consists of two steps: addition/subtraction and multiplication/division. By solving the equations correctly, students can identify the correct direction to proceed through the maze.
Providing an answer key for the two-step equation maze is an essential component of this activity. The answer key allows students to self-assess their work and receive instant feedback. It also serves as a valuable tool for educators to assess students’ understanding of solving two-step equations.
The two-step equation maze answer key typically includes the correct solutions for each equation in the maze, as well as the correct path to the exit. In some cases, additional explanations and steps may be included to help students understand the process of solving the equations. This answer key serves as both a guide and a learning resource, allowing students to learn from their mistakes and improve their problem-solving skills.
What are two step equations?
A two-step equation is a mathematical equation that involves two operations to solve for an unknown variable. These equations are called “two-step” because they require two different steps to isolate the variable.
In a two-step equation, you will typically encounter addition or subtraction, followed by multiplication or division. The goal is to simplify the equation by performing the inverse operation and isolating the variable on one side of the equation.
For example, let’s consider the following equation: 3x + 5 = 17. To solve this equation, you would first subtract 5 from both sides to eliminate the constant term. This gives you 3x = 12. Then, you would divide both sides by 3 to solve for x. The solution to this equation is x = 4.
Two-step equations are commonly used in algebra to solve real-world problems and find unknown values. They require a deeper understanding of mathematical operations and the ability to apply them in a step-by-step process.
Solving Two-Step Equations Step by Step
Solving two-step equations involves performing two separate operations to isolate the variable. The goal is to get the variable by itself on one side of the equation. Let’s break it down step by step:
Step 1: Combine like terms. If there are any like terms on either side of the equation, simplify them by combining or canceling them out. This step helps to make the equation easier to solve.
Step 2: Undo addition or subtraction. If the variable is being added or subtracted, undo this operation by performing the opposite operation. If the variable is being added, subtract the same value from both sides of the equation. If the variable is being subtracted, add the same value to both sides.
Step 3: Undo multiplication or division. If the variable is being multiplied or divided, undo this operation by performing the opposite operation. If the variable is being multiplied, divide both sides of the equation by the same value. If the variable is being divided, multiply both sides by the same value.
Using these steps, continue simplifying the equation until the variable is isolated on one side and the solution is on the other side. Remember to perform the same operation to both sides of the equation to maintain equality. This method helps to systematically solve two-step equations and find the value of the variable.
First step: Undo addition or subtraction
When solving a two-step equation, the first step is to undo any addition or subtraction that is happening to the variable. This step is important because it helps isolate the variable on one side of the equation.
To undo addition, you need to subtract the same number from both sides of the equation. For example, if the equation is 2x + 3 = 9, you would subtract 3 from both sides to get 2x = 6.
To undo subtraction, you need to add the same number to both sides of the equation. For example, if the equation is 4x – 5 = 11, you would add 5 to both sides to get 4x = 16.
By undoing addition or subtraction, you are able to simplify the equation and make it easier to solve. Once the addition or subtraction is undone, you can move on to the next step of solving the equation, which is usually undoing multiplication or division.
Second step: Undo multiplication or division
After solving the first step of a two-step equation, which involves undoing addition or subtraction, you move on to the second step. In this step, you undo multiplication or division to isolate the variable.
If the equation involves multiplication, you can undo it by dividing both sides of the equation by the coefficient of the variable. For example, if the equation is 5x = 20, you divide both sides by 5 to get x = 4, which is the solution. This step helps in isolating the variable and finding its exact value.
Similarly, if the equation involves division, you can undo it by multiplying both sides of the equation by the denominator. For instance, if the equation is x/3 = 6, you multiply both sides by 3 to cancel out the division and obtain x = 18 as the solution. Undoing multiplication or division allows you to reverse the operations and work towards finding the unknown variable.
It’s important to remember that when performing these operations, you must apply them to both sides of the equation to maintain equality. This ensures that you find the correct solution to the equation. Undoing multiplication or division is an essential step in solving two-step equations and helps to simplify the problem and find the variable’s value.
Two Step Equation Maze Activity
Two step equation maze activity is a fun and engaging way for students to practice solving two step equations. This activity requires students to navigate through a maze by solving equations in order to find the correct path. It provides a hands-on approach to learning, allowing students to apply their math skills in a real-world context.
The activity starts with a maze that contains various equations written on the walls. Students are then given a set of equations to solve and must find the solution that matches one of the pathways in the maze. They must carefully analyze each equation, perform the necessary operations, and simplify the equations step by step to find the correct solution. This activity helps students develop a deeper understanding of the concept of two step equations and strengthens their problem-solving skills.
By engaging in this maze activity, students are able to visualize the process of solving equations and reinforce their knowledge of the steps involved. They also learn to think critically and make logical decisions as they navigate through the maze. This hands-on approach to learning helps students retain the information better and promotes a more active and participatory learning experience.
In conclusion, the two step equation maze activity is a valuable tool for teaching and reinforcing the concept of solving two step equations. It allows students to engage with the material in a more interactive way and helps them develop important problem-solving skills. This activity can be used in both classroom settings and as a supplementary resource for independent practice. Overall, it provides an effective and enjoyable way for students to master the concept of two step equations.
How does the two step equation maze work?
The two step equation maze is a mathematical activity designed to help students practice solving two step equations. It consists of a maze with various equations written on it, and the goal is for students to find a path from the entrance to the exit by solving each equation correctly.
Each equation in the maze requires two steps to solve. The steps typically involve performing inverse operations to isolate the variable. The equations may involve addition, subtraction, multiplication, or division. Students must carefully follow the correct order of operations to simplify each equation and find the value of the variable.
The maze itself is designed with multiple paths and dead ends to provide an additional challenge. Students must choose the correct path based on their solutions to each equation. If they make a mistake and choose the wrong path, they may encounter a dead end and have to backtrack to find the correct path.
Completing the two step equation maze requires both mathematical skills and critical thinking. Students must analyze each equation, apply the appropriate operations, and make strategic decisions about which path to take in the maze. This activity helps reinforce students’ understanding of two step equations and encourages problem-solving skills.
Why is the two step equation maze useful for learning?
The two step equation maze is a valuable tool for learning because it allows students to practice and reinforce their understanding of solving two-step equations in a fun and engaging way. By navigating through the maze and solving equations at each step, students are able to apply their knowledge and skills in a real-life context, making the learning experience more meaningful and memorable.
Additionally, the maze format provides an opportunity for students to develop problem-solving and critical thinking skills. As they encounter different equations and obstacles in the maze, students are challenged to analyze the problem, formulate a plan, and execute their solution. This process not only strengthens their mathematical abilities but also fosters skills that are transferable to other areas of their academic and personal lives.
The visual and interactive nature of the two step equation maze also caters to different learning styles. Some students may find it easier to understand and remember concepts when they are presented in a visual format, while others may benefit from the hands-on nature of navigating through the maze. By appealing to different learning styles, the maze provides an inclusive learning environment where all students can actively participate and succeed.
Furthermore, the two step equation maze encourages teamwork and collaboration. Students can work together in pairs or small groups to solve the equations and find their way through the maze. This collaborative approach promotes communication, cooperation, and the sharing of different strategies and perspectives. It also helps students develop their interpersonal skills, such as active listening and respectful communication, which are essential for success not only in mathematics but in many other aspects of life.
In conclusion, the two step equation maze is a valuable learning tool that combines mathematical practice with problem-solving, critical thinking, visual learning, and teamwork. By engaging students in a fun and interactive way, the maze helps them develop a deeper understanding of two-step equations and equips them with valuable skills for their academic and personal journeys.
Answer key for the two step equation maze

In the two-step equation maze, students are required to solve various equations by applying two different operations. The answer key provides the solutions to the equations presented in the maze, allowing students to check their work and ensure accuracy.
The answer key typically includes a list of equations and their corresponding solutions. Each equation is labeled, making it easy for students to match their own work with the correct answer. The solutions may be expressed as a simplified number or a variable, depending on the equation.
For example, if one of the equations in the maze is “2x + 5 = 15”, the corresponding solution in the answer key may be “x = 5”. This indicates that when the equation is simplified and solved, the value of x is equal to 5.
The answer key serves as an educational resource that provides immediate feedback to students. By comparing their own solutions to the answers in the key, students can identify any mistakes or errors they may have made. This allows for self-correction and encourages a deeper understanding of the concepts involved in solving two-step equations.
In addition to helping students review their work, the answer key can also be used by teachers as a reference tool. It allows them to quickly assess whether a student has correctly solved the equations in the maze and provides an opportunity for targeted instruction and intervention if necessary.
Overall, the answer key for the two-step equation maze is a valuable resource that aids both students and teachers in the learning and teaching process. It promotes student engagement, self-assessment, and a better understanding of algebraic concepts.