When studying geometry, an essential concept to grasp is the understanding of points, lines, and planes. These fundamental elements serve as the backbone for all geometric structures and relationships. By comprehending the key principles behind points, lines, and planes, students gain the foundation necessary for further explorations in geometry.
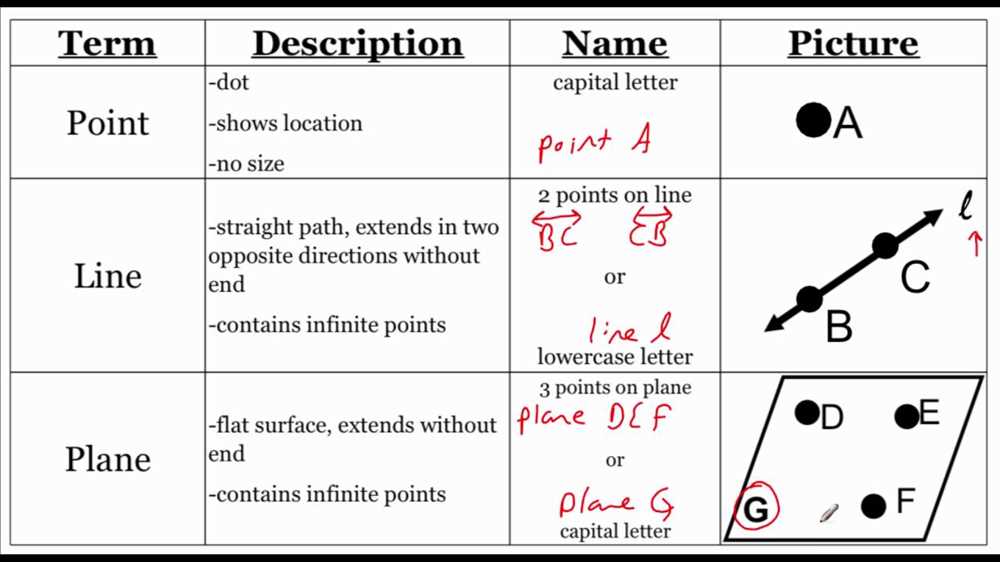
Firstly, points are considered the most basic building blocks in geometry. They possess no size or shape and are represented by a dot. Points are used to indicate specific locations in space and are labeled with a unique letter. Throughout geometric calculations and proofs, points act as the foundation for defining lines and planes.
On the other hand, lines are infinite collections of points that extend indefinitely in two opposite directions. They are represented by a straight line with arrows on each end and are labeled with any two points on the line or a lowercase letter. Understanding lines involves recognizing properties such as length, midpoint, and slope. Lines can intersect, forming various angles and connecting points to create shapes.
Lastly, planes are flat surfaces extending infinitely in all directions. They are characterized by their length and width and are represented by a parallelogram or a letter in an italic font. Planes can be described as a combination of an infinite number of points arranged systematically. They can intersect with lines and other planes, leading to further geometric interpretations and solutions.
In conclusion, acquiring a solid understanding of points, lines, and planes is crucial for all students entering the world of geometry. Points serve as the foundation, while lines and planes extend from this core concept, allowing for further geometric exploration. By grasping the principles behind points, lines, and planes, individuals can confidently navigate the complexities of geometry and develop a strong foundation for further mathematical studies.
Understanding Points Lines and Planes Answer Key
In geometry, understanding points, lines, and planes is crucial for grasping the basic concepts and principles of the subject. To fully comprehend these fundamental elements, it is essential to have access to an answer key that provides clear explanations and solutions to exercises and problems. The Understanding Points Lines and Planes Answer Key serves as a valuable resource for students and teachers alike, offering a comprehensive guide to understanding and applying these geometric concepts.
The answer key begins by defining and explaining the concept of a point in geometry. A point is a specific location in space that does not have any size or dimensions. It is represented by a dot and is typically labeled with a capital letter. Through detailed explanations and examples, the answer key helps students understand the characteristics and properties of points, such as the fact that any two points determine a line.
The answer key then moves on to discussing lines, which are infinitely long, straight paths in space. A line is determined by two distinct points and extends infinitely in both directions. The answer key provides students with a clear understanding of the different types of lines, such as intersecting lines, parallel lines, and perpendicular lines. It also covers concepts such as line segments and rays, which are important in understanding the relationship between points and lines.
Lastly, the answer key delves into the concept of planes. A plane is a two-dimensional flat surface that extends infinitely in all directions. It is determined by three non-collinear points or by a line and a point not on that line. The answer key explains the properties and characteristics of planes, including parallel planes, intersecting planes, and skew lines. It also provides examples and exercises to reinforce the understanding of these concepts.
In conclusion, the Understanding Points Lines and Planes Answer Key offers a comprehensive and detailed guide to comprehending the fundamental geometric concepts of points, lines, and planes. Through clear explanations and examples, it helps students deepen their understanding and apply these concepts to solve geometry problems effectively.
Defining Points
A point is one of the basic building blocks in geometry. It is a location in space and is represented by a dot. A point is considered to have no size or dimension; it is simply a precise position.
Key phrases:
- A point is a location in space.
- A point is represented by a dot.
- A point has no size or dimension.
- A point is a precise position.
When working with points in geometry, it is important to keep in mind that they are abstract concepts. They do not have any physical existence, but they help in describing and understanding different aspects of space and shapes. Points are often used to define other geometric objects, such as lines and planes.
Points can be named using capital letters, such as A, B, C, or any other letter chosen. The order of the letters does not matter, as long as each letter represents a unique point. This naming convention helps in distinguishing between multiple points and referring to them in calculations and proofs.
In addition to their names, points can also have coordinates, which are numerical values that represent their position in relation to a coordinate system. Coordinates are often used in more advanced geometry and are expressed as ordered pairs or triplets, depending on the dimensionality of the space.
In conclusion, points are fundamental elements in geometry that represent precise positions in space. They have no size or dimension and are used to define and describe other geometric objects. Points can be named with letters and can have coordinates that indicate their position in relation to a coordinate system. Understanding points is essential in building a solid foundation in geometry.
Identifying Lines
In geometry, lines are fundamental elements that play a crucial role in understanding the relationships between points and planes. A line is defined as a straight path that extends indefinitely in both directions. It can be represented by a series of points that are collinear, meaning they lie on the same line.
There are different types of lines that can be identified based on their properties and characteristics. One common type is a straight line, which has no curves or angles. It can be thought of as a series of points that are equidistant from each other, creating a perfectly straight path. Another type is a line segment, which is a portion of a line with distinct endpoints. Unlike a straight line, a line segment has a definite length and can be measured.
- Rays: A ray is another type of line that has a distinct starting point and extends indefinitely in one direction. It can be thought of as a half-line, with one endpoint and one direction.
- Parallel Lines: Parallel lines are lines that never intersect, no matter how far they are extended. They always maintain the same constant distance between each other.
- Perpendicular Lines: Perpendicular lines are lines that intersect at a right angle, creating four 90-degree angles. They have a unique property where the product of their slopes is equal to -1.
By understanding the properties and characteristics of lines, we are able to analyze and solve various geometric problems. Lines allow us to measure distances, determine angles, and identify patterns in shapes and figures. They are an essential component of geometry and provide a foundation for further mathematical understanding.
Describing Line Segments
A line segment is a part of a line that is bounded by two distinct points, known as the endpoints of the segment. In geometry, line segments are often described using specific terminology and notation to accurately convey their properties and characteristics.
When describing a line segment, it is important to specify its length, which can be determined by finding the distance between its endpoints. For example, if a line segment has endpoints A and B, its length can be denoted as AB or the absolute value of the difference between the coordinates of A and B.
To differentiate between line segments with the same length, they can be named using lowercase letters or labeled with a single bar above the letters representing their endpoints. For instance, a line segment with endpoints A and B can be referred to as segment AB or line AB.
In addition to length, line segments can also be described by their midpoint – the point that divides the segment into two congruent parts. The midpoint of a line segment AB is denoted as M and can be found by taking the averages of the coordinates of A and B.
Furthermore, line segments can be classified based on their orientation and position relative to other segments or lines. They can be either horizontal, vertical, diagonal, or inclined. Moreover, two line segments can be parallel if they lie in the same plane and never intersect. Conversely, two line segments are said to be perpendicular if they intersect at a right angle.
Overall, describing line segments involves specifying their length, naming conventions, midpoint, orientation, and position relative to other segments or lines. This precise and detailed description helps to accurately represent and analyze geometric figures and relationships.
Recognizing Parallel Lines

Parallel lines are a fundamental concept in geometry. They are two lines in a two-dimensional plane that never intersect, no matter how far they are extended. Recognizing parallel lines is important in various applications, such as determining if two lines represent the same slope or finding alternate interior angles.
To recognize parallel lines, there are a few key characteristics to look for. First, parallel lines have the same slope. The slope is a measure of how steep a line is and is represented by the coefficient of the x term in the equation of the line. If two lines have the same coefficient of x, they have the same slope and therefore are parallel.
Another way to recognize parallel lines is by looking at their equations. If two lines have the same y-intercept and different slopes, they are parallel. The y-intercept is the point where the line crosses the y-axis. If two lines have the same y-intercept but different slopes, they will never intersect and are therefore parallel.
Recognizing parallel lines is an essential skill in geometry and has numerous practical applications. It allows for easier identification of patterns and relationships between lines and helps solve various geometry problems. By understanding the key characteristics and properties of parallel lines, one can confidently work with them in different mathematical contexts.
Understanding Intersecting Lines
Intersecting lines are a fundamental concept in geometry that play a significant role in understanding the relationships and properties of points, lines, and planes. In geometry, a line is defined as a straight path that extends infinitely in both directions. When two lines cross each other at a particular point, they are said to intersect.
Intersecting lines form an angle at the point of intersection. The measurement of this angle can provide valuable information about the relationship between the lines. If the angle measures 90 degrees, the lines are perpendicular. If the angle is less than 90 degrees, the lines are considered acute, and if the angle is greater than 90 degrees, the lines are considered obtuse.
When two lines intersect, they create multiple pairs of opposite angles. These angles are equal in measure, meaning that they have the same degree of rotation. Additionally, the sum of adjacent angles formed by intersecting lines is always equal to 180 degrees. This property is known as the linear pair postulate.
Intersecting lines also provide the basis for understanding other geometric concepts. For example, the intersection of two lines can form a triangle or a quadrilateral. It can also help in determining the position of points relative to each other and identifying parallel lines.
In conclusion, understanding intersecting lines is essential in geometry as it helps analyze angles, determine shapes, and establish relationships between points, lines, and planes. By studying the properties and characteristics of intersecting lines, we can deepen our understanding of geometric concepts and apply them to solve complex problems.
Exploring Perpendicular Lines
In geometry, perpendicular lines play a significant role in understanding the relationships between points, lines, and planes. Two lines are said to be perpendicular if they intersect at a right angle, forming four 90-degree angles. This special relationship between lines can be explored and understood through various properties and theorems.
Definition: Perpendicular lines are two lines that intersect to form right angles.
Property 1: The slopes of two perpendicular lines are negative reciprocals of each other. This means that if the slope of one line is m, the slope of the perpendicular line is -1/m.
Understanding perpendicular lines helps us solve problems involving geometric figures, such as finding the distance between a point and a line or determining if two lines are parallel or perpendicular. It also helps in real-life applications, such as designing buildings, surveying land, or creating computer graphics.
By exploring the properties and relationships of perpendicular lines, mathematicians and engineers can make accurate calculations and create precise designs. The study of perpendicular lines is an important part of geometry and plays a crucial role in various fields and industries.
Introducing Planes
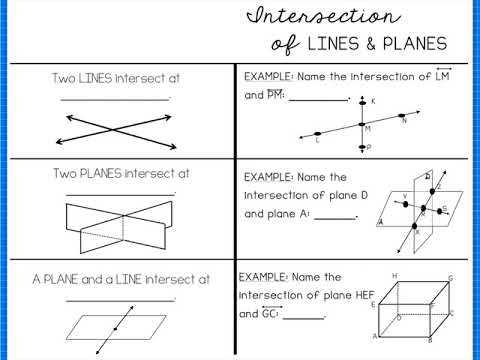
A plane is a two-dimensional flat surface that extends infinitely in all directions. It is formed by an infinite number of points and is the basis for many geometrical concepts and calculations. Understanding planes is crucial in the field of mathematics, as it helps us analyze and solve problems involving spatial relationships.
In geometry, a plane can be described using several different methods. One common way is by defining three non-collinear points, also known as a non-collinear set. These points determine a unique plane, and any additional point on this plane can be represented as a combination of the original three points and their corresponding values.
Another way to define a plane is by using a line that is not parallel to the plane. If a line intersects a plane at a single point, it is said to lie on the plane. This can be visualized as a pencil being pushed through a sheet of paper – the pencil (line) enters and leaves the paper at a single point, indicating that it lies on the plane.
A plane can also be represented using an equation. The equation of a plane in three-dimensional space is typically in the form of Ax + By + Cz + D = 0, where A, B, C, and D are constants. This equation allows us to determine whether a point lies on the plane or not by substituting its coordinates into the equation.
Understanding planes is fundamental in various areas of mathematics, such as coordinate geometry, vector algebra, and calculus. By knowing how to identify, describe, and work with planes, mathematicians and scientists can solve complex problems and make accurate predictions in various fields, including physics, engineering, and computer science.