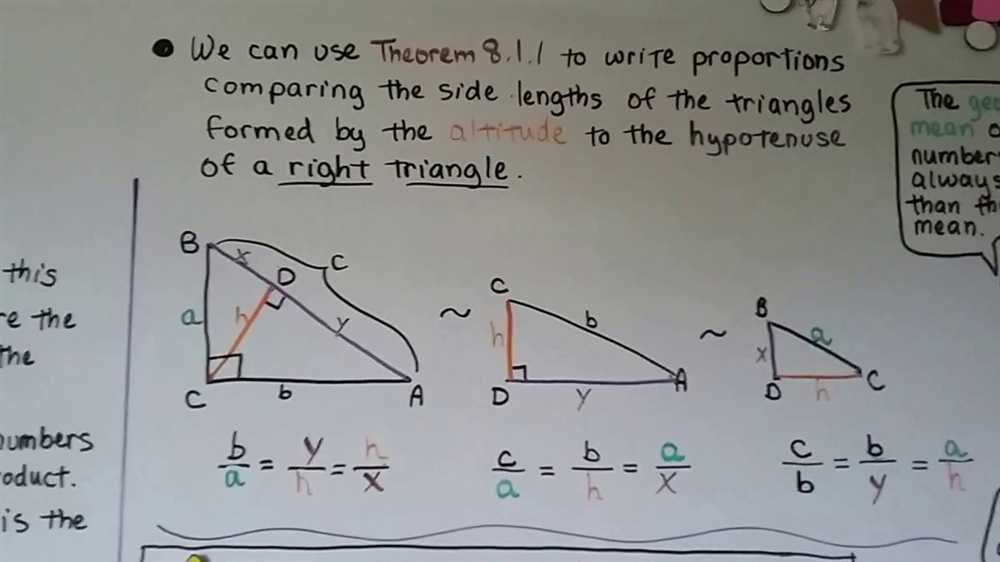
Understanding the concepts of right triangle trigonometry is essential for solving various mathematical problems involving angles and distances. In this article, we will provide the answer key for Unit 3, focusing on right triangle trigonometry. We will explore the relationship between angles, sides, and trigonometric functions such as sine, cosine, and tangent.
By mastering this answer key, you will be able to solve problems involving missing angles or sides in right triangles, calculate trigonometric ratios, find the lengths of unknown sides, and determine the measures of angles. These skills are crucial for fields such as engineering, architecture, physics, and navigation, where precise measurements and calculations are required.
The answer key will include step-by-step solutions and explanations for each problem, allowing you to understand the underlying principles and apply them to similar problems in the future. Whether you are a student studying trigonometry or someone seeking a refresher, this answer key will help you develop a strong foundation in right triangle trigonometry.
Unit 3 Right Triangle Trigonometry Answer Key: Everything You Need to Know
Trigonometry is a branch of mathematics that deals with the relationships between the angles and sides of triangles. In Unit 3 of the study of right triangle trigonometry, students learn about the key concepts and formulas to solve problems involving right triangles. This answer key provides all the necessary information and solutions to help students understand and master the material.
The answer key includes the definitions of important trigonometric terms such as sine, cosine, and tangent, as well as the relationships between these functions. It also provides step-by-step instructions on how to use these trigonometric functions to find missing sides or angles of right triangles. The key covers various scenarios, including finding the length of a side when the opposite angle and another side are known, or finding an angle when the lengths of two sides are given.
In addition to the explanations and formulas, the answer key includes practice problems with detailed solutions. These problems cover a range of difficulty levels, allowing students to practice their skills and gain confidence in applying the concepts they have learned. The solutions provided in the answer key allow students to check their work and understand the steps involved in solving each problem.
The Unit 3 Right Triangle Trigonometry Answer Key is an essential tool for students studying trigonometry. It provides a comprehensive overview of the material covered in Unit 3 and offers a wealth of practice problems and solutions. With the help of this answer key, students can strengthen their understanding of right triangle trigonometry and improve their problem-solving skills.
Understanding Right Triangle Trigonometry
Right triangle trigonometry is a branch of mathematics that deals with the relationships between the angles and sides of right triangles. In a right triangle, one of the angles is always 90 degrees, and the other two angles are acute. Right triangle trigonometry involves using these angles and the lengths of the sides of the triangle to find unknown angles or side lengths.
One of the fundamental concepts in right triangle trigonometry is the use of ratios involving the sides of the triangle. The three primary trigonometric ratios are sine, cosine, and tangent, commonly written as sin, cos, and tan. The sine of an angle is equal to the ratio of the length of the side opposite the angle to the length of the hypotenuse, the cosine is equal to the ratio of the length of the side adjacent to the angle to the length of the hypotenuse, and the tangent is equal to the ratio of the length of the side opposite the angle to the length of the side adjacent to the angle.
These trigonometric ratios can be used to solve a variety of problems involving right triangles. For example, given the length of one side and the measure of one acute angle of a right triangle, the lengths of the other sides can be found using trigonometric ratios. Similarly, if the lengths of two sides of a right triangle are known, the measures of the angles can be determined using inverse trigonometric functions.
Overall, understanding right triangle trigonometry is essential for many practical applications, such as engineering, architecture, and physics. It provides a mathematical framework for analyzing and solving problems involving right triangles, allowing us to make accurate calculations and predictions in various fields.
The Importance of the Unit 3 Right Triangle Trigonometry Answer Key

When learning about right triangle trigonometry, having access to an answer key is incredibly important. The answer key provides students with a way to check their work and ensure that they are on the right track. It allows them to confirm whether they have solved the problems correctly or if they need to make corrections. Additionally, the answer key serves as a valuable learning tool, as it allows students to understand the steps and logic behind solving the problems.
The Unit 3 Right Triangle Trigonometry Answer Key is particularly crucial because it covers a fundamental topic in trigonometry. Right triangles are prevalent in various fields such as engineering, physics, architecture, and navigation. Understanding and applying trigonometric principles to solve problems involving right triangles is necessary for success in these fields. The Unit 3 Right Triangle Trigonometry Answer Key enables students to develop a solid foundation in this subject, helping them excel in further studies and future careers.
With the Unit 3 Right Triangle Trigonometry Answer Key, students can confidently approach their assignments and tests. It provides them with an opportunity to practice and reinforce their understanding of the concepts and formulas related to right triangle trigonometry. Students can review their mistakes, learn from them, and improve their problem-solving skills. Furthermore, having access to the answer key empowers students to take responsibility for their own learning, as they can proactively identify areas where they need further practice or clarification.
In conclusion, the Unit 3 Right Triangle Trigonometry Answer Key is an invaluable resource for students studying trigonometry. It allows them to check their work, learn from their mistakes, and build a solid foundation in this important branch of mathematics. Whether used as a reference or as a practice tool, the answer key plays a crucial role in enhancing students’ understanding and mastery of right triangle trigonometry concepts.
Key Concepts in Unit 3 Right Triangle Trigonometry
Unit 3 of right triangle trigonometry covers several key concepts that are fundamental to understanding the relationships between angles and sides in a right triangle. These concepts are essential in applications such as solving real-world problems involving triangles, physics, and engineering.
Trigonometric Ratios:
One of the key concepts in right triangle trigonometry is understanding the trigonometric ratios. These ratios relate the angles in a right triangle to the ratios of the lengths of its sides. The three main ratios are sine, cosine, and tangent. The sine of an angle is defined as the ratio of the length of the side opposite the angle to the length of the hypotenuse. The cosine of an angle is defined as the ratio of the length of the adjacent side to the length of the hypotenuse. Lastly, the tangent of an angle is defined as the ratio of the length of the side opposite the angle to the length of the adjacent side. These ratios help us solve for angles and side lengths in right triangles.
Trig Inverse Functions:
An important concept covered in this unit is the use of inverse trigonometric functions. These functions allow us to find the measure of an angle given the ratio of the lengths of the sides or vice versa. The inverse sine function, denoted as sin⁻¹, returns the measure of an angle whose sine is a given value. Similarly, the inverse cosine function, denoted as cos⁻¹, returns the measure of an angle whose cosine is a given value. Lastly, the inverse tangent function, denoted as tan⁻¹, returns the measure of an angle whose tangent is a given value. Inverse trigonometric functions are useful when solving for angles or side lengths in right triangles.
Trigonometric Identities:
In unit 3, we also study various trigonometric identities that help simplify expressions involving trigonometric functions. Some common identities include the Pythagorean identity, which states that the square of the sine of an angle plus the square of the cosine of the angle is always equal to 1. Another important identity is the reciprocal identity, which states that the cosecant of an angle is equal to the reciprocal of the sine of the angle, the secant of an angle is equal to the reciprocal of the cosine of the angle, and the cotangent of an angle is equal to the reciprocal of the tangent of the angle. Trigonometric identities are useful when simplifying complex trigonometric expressions or proving trigonometric equations.
In conclusion, unit 3 of right triangle trigonometry covers key concepts such as trigonometric ratios, trigonometric inverse functions, and trigonometric identities. These concepts are essential in understanding the relationships between angles and sides in a right triangle and are used in various applications in mathematics, physics, and engineering.
Exploring the Unit 3 Right Triangle Trigonometry Answer Key
When studying right triangle trigonometry, it is important to have a comprehensive answer key to check your work and ensure accuracy. The Unit 3 Right Triangle Trigonometry Answer Key provides students with the correct solutions and explanations for the various problems and exercises encountered throughout the unit. This answer key serves as a valuable resource for students to assess their understanding and identify any areas that require further practice or clarification.
The Unit 3 Right Triangle Trigonometry Answer Key is organized into different sections, each corresponding to a specific topic or concept covered in the unit. This allows students to easily locate the relevant answers and explanations for the problems they are working on. Whether it is calculating angles, side lengths, or solving word problems using trigonometric ratios, the answer key provides step-by-step solutions to guide students through the process.
The answer key not only contains the final answers, but also includes detailed explanations and reasoning behind each step taken to arrive at the solution. This helps students understand the underlying concepts and principles of right triangle trigonometry, enabling them to apply this knowledge to similar problems in the future. The thoroughness of the answer key ensures that students not only know the correct answer, but also comprehend how to arrive at it.
Furthermore, the Unit 3 Right Triangle Trigonometry Answer Key can be used by teachers as a valuable teaching tool. It provides a reference for teachers to check and verify the correctness of student solutions, and can also serve as a guide for explaining complex concepts and problem-solving strategies to students. By utilizing the answer key in the classroom, teachers can provide immediate feedback and support to students, promoting a deeper understanding of right triangle trigonometry.
In conclusion, the Unit 3 Right Triangle Trigonometry Answer Key is an essential resource for both students and teachers. It ensures accuracy in problem-solving, provides thorough explanations, and promotes a deeper understanding of right triangle trigonometry. Whether used for self-assessment or as a teaching aid, this answer key is a valuable tool in the study of this important mathematical concept.
Common Mistakes to Avoid in Unit 3 Right Triangle Trigonometry

In Unit 3 of right triangle trigonometry, it is important to be aware of common mistakes that students often make. By being mindful of these errors, you can improve your understanding and accuracy in this topic. Here are some common mistakes to avoid:
1. Confusing the sides and angles of a right triangle:
One common mistake is mixing up the names and properties of the sides and angles in a right triangle. It’s crucial to understand the specific terminology and relationships between the hypotenuse, opposite, and adjacent sides, as well as the angles that correspond to them. Familiarize yourself with the definitions and remember to use the correct terms when solving trigonometric problems.
2. Forgetting to check the units:
Another common mistake is failing to check the units in the problem or in the final answer. Trigonometric ratios involve ratios of lengths, which means that the units of measurement must match. Double-check that all lengths are in the same units (e.g., centimeters, meters, or inches) before using trigonometric functions. Also, ensure that the units in the final answer are consistent with the original problem.
3. Misusing trigonometric ratios:

Using the wrong trigonometric ratio is a frequent error. Make sure to carefully identify the given information and determine which trigonometric function is appropriate to use. For example, if you have the length of the opposite side and the hypotenuse, you should use the sine function, not the cosine or tangent. Always double-check your calculations to ensure that you are using the correct trigonometric ratio for the given problem.
4. Rounding errors:
In trigonometry, rounding errors can accumulate and lead to incorrect answers. To minimize rounding errors, carry as many decimal places as possible throughout the calculations, only rounding to the appropriate number of significant figures at the end. Additionally, when using a calculator, make sure it is set to the correct angle mode (degrees or radians) to obtain accurate results.
- By avoiding these common mistakes, you can enhance your understanding of right triangle trigonometry and improve your problem-solving skills in this unit.
- Remember to carefully review your work, be familiar with the specific terminology and concepts, and double-check your calculations to ensure accuracy.
- As you practice, these common mistakes will become easier to avoid, and you’ll develop a more solid foundation in right triangle trigonometry.
Tips and Tricks for Solving Right Triangle Trigonometry Problems

Right triangle trigonometry problems can be challenging, but with a few helpful tips and tricks, you can approach them with confidence. Here are some strategies to keep in mind when solving these types of problems:
1. Identify the known and unknown quantities:
Before diving into the problem, carefully read and understand the given information. Identify what values are given (known quantities) and what values you need to find (unknown quantities). This will help you determine which trigonometric ratio to use and how to set up the equation.
2. Use the correct trigonometric ratio:
Depending on the known and unknown quantities, you will need to choose the appropriate trigonometric ratio: sine, cosine, or tangent. Recall that sine is opposite/hypotenuse, cosine is adjacent/hypotenuse, and tangent is opposite/adjacent. Use the ratio that relates the known and unknown quantities.
3. Check for special right triangles:
In some cases, the given triangle may be a special right triangle, such as a 30-60-90 triangle or a 45-45-90 triangle. These triangles have specific ratios that can simplify the calculations. If you notice any familiar angles or side lengths, apply the corresponding special right triangle ratios.
4. Use Pythagorean theorem if necessary:
If the problem involves finding a missing side length, you may need to use the Pythagorean theorem. Remember that in a right triangle, the sum of the squares of the lengths of the two legs is equal to the square of the length of the hypotenuse. Use this theorem to solve for the missing side length.
5. Pay attention to units and rounding:
When solving right triangle trigonometry problems, make sure to pay attention to units and rounding. Check whether the answer is expected in degrees or radians, and adjust your calculations accordingly. Also, consider the level of precision required and round your final answer appropriately.
By keeping these tips and tricks in mind, you can approach right triangle trigonometry problems with confidence and successfully solve them. Practice applying these strategies to various problem scenarios to strengthen your understanding of this mathematical concept.