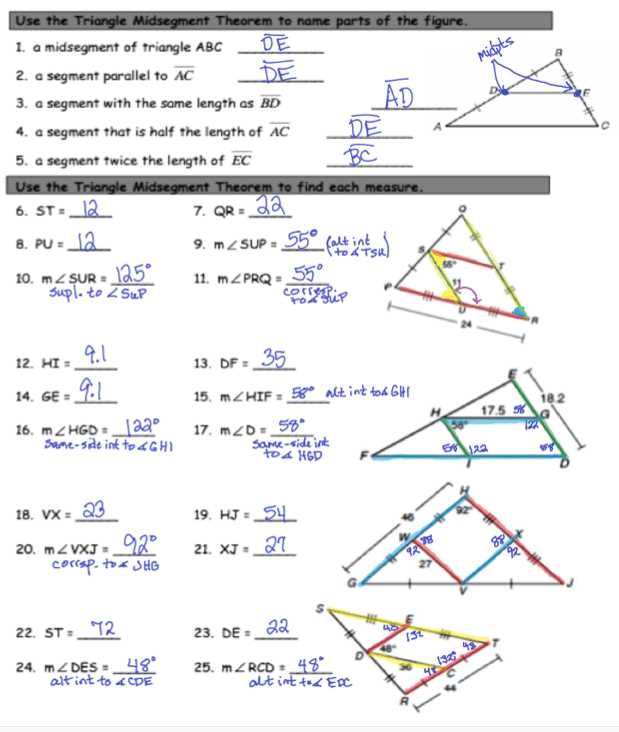
Understanding the relationships between the sides and angles of triangles is a fundamental concept in geometry. In Unit 5, students dive deeper into this topic and explore various properties and theorems that govern these relationships. Homework 5 is a critical component of this unit, as it offers students the opportunity to apply their knowledge and test their understanding through a series of challenging problems.
With the answer key for Unit 5 Relationships in Triangles Homework 5, students can check their work and verify their solutions. This invaluable tool helps students identify any mistakes and learn from them, strengthening their understanding of the material. By effectively utilizing the answer key, students can enhance their problem-solving skills and boost their confidence in geometry.
The answer key for Unit 5 Relationships in Triangles Homework 5 provides step-by-step explanations for each problem, ensuring that students grasp the concepts and techniques required to arrive at the correct answers. Whether it’s determining the congruence of triangles, finding missing angles or sides, or applying the Pythagorean theorem, this answer key serves as a comprehensive guide for students to master the principles of triangle relationships.
Unit 5 Relationships in Triangles Homework 5 Answer Key
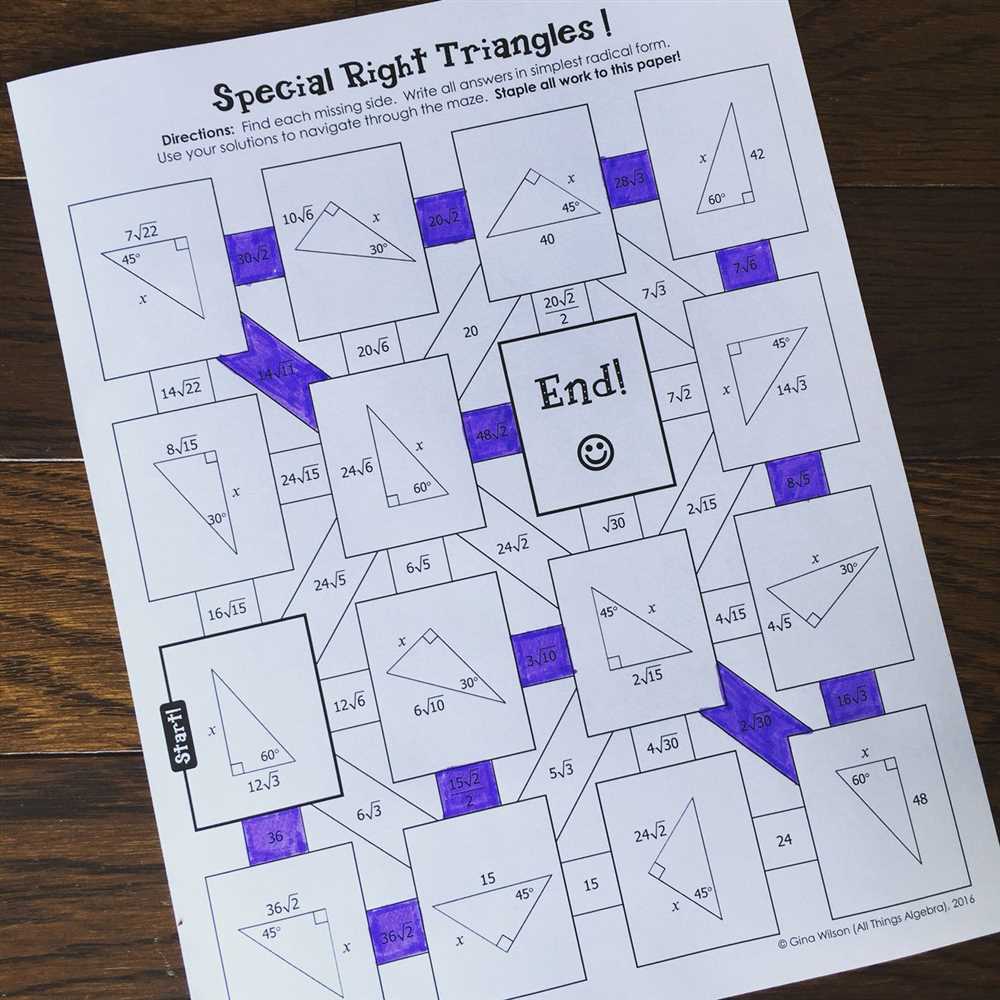
In Unit 5 of our geometry course, we have been exploring the relationships in triangles and how to solve problems involving these relationships. Homework 5 focused on applying the concepts we have learned so far to various types of triangles.
The answer key for Homework 5 is provided below, with a brief explanation of each problem:
- Problem 1: Find the missing angle in a triangle where the other two angles are 40° and 70°. The missing angle is 70°, as the sum of the three angles in any triangle is always 180°.
- Problem 2: Determine the type of triangle given the lengths of its sides: 4 cm, 4 cm, and 6 cm. The triangle is an isosceles triangle, as it has two sides of equal length.
- Problem 3: Calculate the height of an equilateral triangle with a side length of 10 cm. The height is equal to √3/2 times the length of one side, so in this case, the height is 10√3/2 cm.
- Problem 4: Find the missing side length in a right triangle with one side measuring 5 cm and the hypotenuse measuring 13 cm. Using the Pythagorean theorem, we can find the missing side to be 12 cm.
These are just a few examples from Homework 5, but they demonstrate the key concepts we have covered in this unit. By understanding the relationships and properties of triangles, we can solve a variety of problems involving them.
Understanding Relationships in Triangles
Triangles are three-sided polygons that have unique relationships between their angles and sides. By understanding these relationships, mathematicians can solve complex geometric problems and make important calculations.
One significant relationship in triangles is the Pythagorean Theorem, which states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. This theorem allows us to find the length of a missing side in a right triangle or determine whether a triangle is a right triangle.
Another important relationship in triangles is the concept of congruence. Two triangles are congruent if their corresponding sides and angles are equal. This means that the triangles have the same shape and size, but they may be oriented differently. Congruent triangles can be used to prove other relationships or to find missing angles and sides in a triangle.
Additionally, triangles have several properties that relate to their angles and sides. For example, the sum of the angles in a triangle is always 180 degrees. This property allows us to find missing angles or determine whether a given set of angles can form a triangle. Triangles also have relationships between their sides, such as the triangle inequality theorem, which states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.
Understanding these relationships in triangles is essential for solving geometric problems and making accurate calculations. Whether you are finding the length of a missing side, proving congruence, or determining the validity of a triangle, knowing these relationships will help you navigate the world of triangles with confidence and precision.
Exploring Angle Relationships in Triangles
In the study of geometry, triangles play a crucial role. They are the most basic polygon, consisting of three sides and three angles. Within a triangle, angles can have various relationships to each other. Understanding these relationships is fundamental to solving geometrical problems and proving theorems.
Adjacent angles: When two angles share a common side, they are called adjacent angles. In a triangle, adjacent angles are often found at the vertices, where two sides meet. The sum of adjacent angles in a triangle is always equal to the third angle.
Supplementary angles: Two angles are supplementary if the sum of their measures is 180 degrees. In a triangle, a pair of angles that are supplementary is called a linear pair. If two angles in a triangle form a linear pair, the third angle is the sum of the measures of the two supplementary angles.
Complementary angles: Two angles are complementary if the sum of their measures is 90 degrees. In a triangle, if one angle is complementary to another angle, the third angle is the difference between 90 degrees and the measure of the complementary angle.
These are just a few examples of the angle relationships that can exist within a triangle. By exploring these relationships, we can gain a deeper understanding of the properties and characteristics of triangles, which can help us solve various geometry problems and proofs.
Solving for Missing Angle Measures
When working with triangles, it is often necessary to find the measure of missing angles. This can be done using various geometric principles and theorems. By understanding these concepts and applying them correctly, we can solve for unknown angle measures in triangles.
One common method to find missing angle measures is by using the Triangle Sum Theorem. According to this theorem, the sum of the three angles in any triangle is always 180 degrees. So, if we know the measures of two angles in a triangle, we can subtract their sum from 180 to find the measure of the third angle.
Another useful theorem for finding missing angle measures is the Exterior Angle Theorem. This theorem states that the measure of an exterior angle of a triangle is equal to the sum of the measures of the two non-adjacent interior angles. By using this theorem, we can find missing angles by subtracting the known measures from the sum of the adjacent angles.
Additionally, there are special relationships between angles in certain types of triangles, such as right triangles and isosceles triangles. In a right triangle, for example, one of the angles is always 90 degrees, which can help determine the measures of the other angles. In an isosceles triangle, where two sides are equal in length, the base angles are also equal in measure.
In conclusion, solving for missing angle measures in triangles involves applying geometric principles and theorems such as the Triangle Sum Theorem and the Exterior Angle Theorem. By understanding these concepts and recognizing special relationships in different types of triangles, we can determine the measures of unknown angles with confidence.
Applying the Angle-Side Relationship in Triangles
- Example 1: Given triangle ABC with angle A measuring 40 degrees, angle B measuring 60 degrees, and side AB measuring 5 units. Using the angle-side relationship, we can find the measure of angle C.
- Example 2: Given triangle XYZ with angle X measuring 75 degrees, angle Y measuring 45 degrees, and side XY measuring 8 units. Using the angle-side relationship, we can find the length of side YZ.
Identifying Congruent Triangles
In geometry, congruent triangles are triangles that have exactly the same size and shape. Identifying congruent triangles is an important skill in geometry as it allows us to prove various geometric theorems and solve problems involving triangles. There are several methods that can be used to identify congruent triangles.
One method is using the Side-Side-Side (SSS) congruence criterion. This criterion states that if the three sides of one triangle are equal in length to the corresponding three sides of another triangle, then the two triangles are congruent. This method is useful when we have the measurements of all three sides of the triangles.
Another method is using the Side-Angle-Side (SAS) congruence criterion. This criterion states that if two sides and the included angle of one triangle are equal in length and measure to the corresponding two sides and included angle of another triangle, then the two triangles are congruent. This method is helpful when we have two sides and the included angle of the triangles.
Additionally, the Angle-Side-Angle (ASA) congruence criterion can be used to identify congruent triangles. This criterion states that if two angles and the included side of one triangle are equal in measure and length to the corresponding two angles and included side of another triangle, then the two triangles are congruent. This method is useful when we have two angles and the included side of the triangles.
By using these congruence criteria, we can confidently identify congruent triangles and apply geometric principles to solve problems and prove theorems involving triangles.
Proving Triangle Congruence with Side-Angle-Side (SAS) and Angle-Side-Angle (ASA) Criteria
In geometry, proving triangle congruence is an important concept that involves demonstrating that two triangles are identical in shape and size. There are several criteria that can be used to prove triangle congruence, including the Side-Angle-Side (SAS) and Angle-Side-Angle (ASA) criteria.
The SAS criteria state that if two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the two triangles are congruent. This means that if we have enough information to show that the corresponding sides and angles are equal, we can conclude that the triangles are congruent.
On the other hand, the ASA criteria state that if two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then the two triangles are congruent. This means that if we have enough information to demonstrate equality between the corresponding angles and the included side, we can prove the congruence of the triangles.
Proving triangle congruence using SAS and ASA criteria involves careful analysis and comparison of the given information. By identifying the corresponding sides and angles, and showing their equality, we can establish the congruence of the triangles. Understanding these criteria is essential for solving geometry problems and analyzing geometric relationships.
Using the Congruent Triangle Relationships
In geometry, congruent triangle relationships can be used to prove various properties and relationships within triangles. Congruent triangles are triangles that have the same size and shape, meaning that all corresponding angles and sides are equal.
One way to use congruent triangle relationships is to prove that two triangles are congruent. This can be done using the SSS (side-side-side) congruence postulate, which states that if the three sides of one triangle are congruent to the three sides of another triangle, then the triangles are congruent. Similarly, the SAS (side-angle-side) and ASA (angle-side-angle) congruence postulates can be used to prove congruence.
Once two triangles are proven to be congruent, their corresponding parts can be considered congruent as well. This means that corresponding angles are equal, corresponding sides are equal, and corresponding diagonals are equal.
Using congruent triangle relationships, we can also prove various properties of triangles. For example, the triangle angle-sum theorem states that the sum of the three interior angles of a triangle is always 180 degrees. This can be proven by using congruent triangle relationships and the fact that corresponding angles of congruent triangles are equal.
Overall, congruent triangle relationships are a powerful tool in geometry that can be used to prove and understand various properties and relationships within triangles. By identifying and utilizing congruent triangles, we can unlock a deeper understanding of the intricate world of triangles and their many properties.
Solving Real-World Problems with Triangle Relationships

Triangle relationships play a crucial role in solving real-world problems, particularly those involving measurements and geometric calculations. By understanding the various relationships that exist within a triangle, individuals can apply their knowledge to solve practical problems in fields such as engineering, architecture, and surveying.
One important relationship is the Pythagorean theorem, which states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. This theorem is widely used in construction and engineering to ensure that structures are stable and secure. For example, when determining the length of a diagonal brace in a roof truss, the Pythagorean theorem can be used to find the precise measurement.
- Example: In a roof truss with a horizontal span of 8 feet and a vertical rise of 6 feet, what is the length of the diagonal brace?
- Solution: By applying the Pythagorean theorem, we can find that the length of the diagonal brace is sqrt(8^2 + 6^2), which is approximately 10 feet.
Triangle relationships also come into play when determining angles and areas. The law of sines and the law of cosines are two formulas that allow individuals to determine the lengths of sides and measures of angles in arbitrary triangles. These formulas are commonly used in navigation, cartography, and satellite tracking. By utilizing these relationships, individuals can accurately calculate distances and angles, ensuring the success of various applications.
In conclusion, understanding triangle relationships is essential for solving real-world problems that involve measurements and geometric calculations. Whether it’s determining the length of a diagonal brace in a roof truss or calculating distances in navigation, triangle relationships provide individuals with the tools they need to solve practical problems and achieve accurate results.