Unit 6: Exponents and Exponential Functions is a crucial module in mathematics that explores the relationship between exponents and their corresponding functions. Understanding the concepts covered in this unit is vital for students to excel in higher-level math courses.
This article presents the answer key for Unit 6, providing students with a valuable resource for checking their work and understanding the solutions to problems they may encounter. By referencing this answer key, students can reinforce their understanding of exponentials and gain confidence in their ability to solve problems related to this topic.
The answer key covers a range of topics, including simplifying expressions with exponents, graphing exponential functions, and solving equations involving exponents. Each answer is thoroughly explained, allowing students to grasp the underlying principles and logic behind each solution.
Unit 6 Exponents and Exponential Functions Answer Key
In Unit 6, we will explore the concept of exponents and exponential functions. Exponents are a way to represent repeated multiplication, where a number is raised to a power. Exponential functions, on the other hand, are functions that have a variable in the exponent.
One key concept in this unit is the product of powers property. This property states that when multiplying two powers with the same base, you can add the exponents. For example, if we have 2^3 * 2^4, we can add the exponents and simplify it to 2^7. This property allows us to simplify expressions and solve equations involving exponents.
Another important concept is the power of a power property. This property states that when raising a power to another power, you can multiply the exponents. For instance, if we have (3^2)^5, we can multiply the exponents and simplify it to 3^10. This property is useful when simplifying expressions with nested exponents.
In addition to these properties, we will also learn about the rules of exponents, such as the quotient of powers and the zero exponent rule. These rules help us simplify and evaluate expressions with exponents more easily.
Throughout this unit, we will practice solving exponential equations, graphing exponential functions, and interpreting exponential growth and decay. By the end of this unit, you should have a solid understanding of exponents and exponential functions and be able to apply them to real-world situations.
What are Exponents?
Exponents are a mathematical notation that helps simplify and represent repeated multiplication of a number by itself. They are also known as powers or indices. In an exponent, the base number is raised to a certain power or exponent, which is written as a superscript above the base number.
For example, in the expression 2^3, the base number is 2 and the exponent is 3. This means that 2 is multiplied by itself three times: 2 x 2 x 2 = 8. In other words, 2^3 is equal to 8.
Exponents are commonly used in many areas of mathematics, science, and engineering. They are especially useful when working with large numbers or very small numbers, as they allow for efficient and concise representation. Exponents also play a crucial role in exponential functions, where the base number is raised to a variable exponent.
Understanding exponents is essential for various mathematical operations, such as simplifying expressions, solving equations, and analyzing exponential growth or decay. It is important to be able to manipulate and solve problems involving exponents accurately to ensure accurate calculations and interpretations in various fields of study.
How to Simplify Exponential Expressions
In mathematics, exponential expressions are equations or expressions that involve exponents. To simplify an exponential expression means to reduce it to its simplest form, making it easier to work with and understand.
There are several basic rules and properties that can be used to simplify exponential expressions:
- Product Rule: When multiplying two exponential expressions with the same base, you can add their exponents. For example, a^m * a^n = a^(m+n).
- Quotient Rule: When dividing two exponential expressions with the same base, you can subtract their exponents. For example, a^m / a^n = a^(m-n).
- Power Rule: When raising an exponential expression to another exponent, you can multiply the exponents. For example, (a^m)^n = a^(m*n).
- Negative Exponents: If an exponent is negative, you can rewrite the expression by taking the reciprocal of the base and changing the sign of the exponent. For example, a^(-m) = 1/a^m.
- Zero Exponent: Any non-zero base raised to the power of zero is equal to 1. For example, a^0 = 1.
By applying these rules and properties, you can simplify complex exponential expressions and make them more manageable. It is important to remember these rules and practice simplifying exponential expressions to improve your algebra skills and solve more advanced mathematical problems.
Understanding the Laws of Exponents
Exponents play a crucial role in mathematics, particularly in the field of algebra. They are used to express numbers raised to a certain power and simplify complex calculations. To fully grasp the concept of exponents, it is essential to understand the laws that govern their operations.
The first law of exponents states that when multiplying two numbers with the same base, the exponents should be added together. For example, 2 to the power of 3 multiplied by 2 to the power of 2 would result in 2 to the power of (3 + 2) = 2 to the power of 5.
The second law of exponents deals with dividing numbers with the same base. In this case, the exponents are subtracted. For instance, 5 to the power of 7 divided by 5 to the power of 4 would simplify to 5 to the power of (7 – 4) = 5 to the power of 3.
The third law of exponents focuses on raising a power to another power. In this scenario, the exponents are multiplied together. For example, (2 to the power of 3) to the power of 4 would simplify to 2 to the power of (3 * 4) = 2 to the power of 12.
The fourth law of exponents pertains to negative exponents. When a number has a negative exponent, it can be written as the reciprocal of the positive exponent. For instance, 3 to the power of -2 would be equivalent to 1 divided by (3 to the power of 2) = 1/3^2.
These laws of exponents form the foundation for solving equations involving exponents and allow for efficient simplification of expressions. By understanding and applying these laws correctly, one can confidently navigate through various mathematical problems that involve exponents and exponential functions.
Solving Exponential Equations
Exponential equations are equations in which the variable appears in the exponent. These equations can be challenging to solve, but there are a few strategies that can help simplify the process. One approach is to use logarithms to isolate the variable and then solve for its value.
To begin solving an exponential equation, it’s important to identify the base of the exponent. If the base is the same on both sides of the equation, you can equate the exponents and solve for the variable. However, if the bases are different, logarithms can be used to bring the variable down from the exponent.
- If the equation is of the form (a^x = b), where (a) and (b) are constants, you can take the logarithm of both sides using the base of your choice (commonly used bases are 10 and (e)). This will give you (log_a(b) = x), where (log_a(b)) represents the logarithm of (b) to the base (a).
- If the equation is of the form (a^x = c), where (a) and (c) are constants, and you want to solve for (x), you can take the logarithm of both sides using the base of your choice. This will give you (log_a(c) = x log_a(a)), and since (log_a(a)) is equal to 1, you simply have (log_a(c) = x).
Once you have isolated the variable using logarithms, you can use the properties of logarithms to simplify the expression further and then solve for the variable. Remember to check your solution by substituting it back into the original equation to ensure that it satisfies the given equation.
Solving exponential equations can be tricky, but with practice and a clear understanding of logarithms, you can become more comfortable with this type of problem and successfully find the solution.
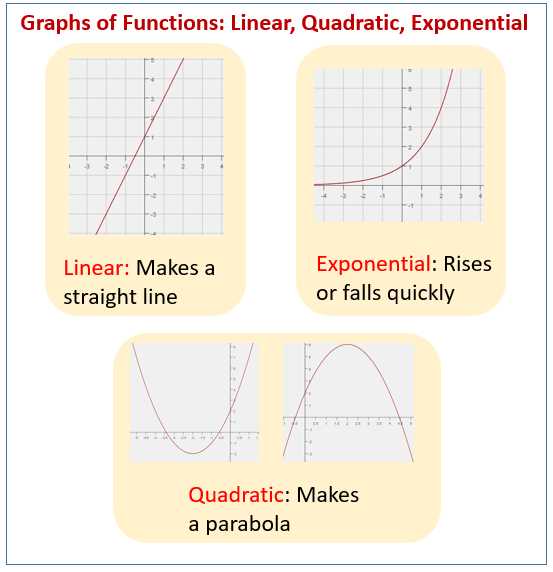
Graphing Exponential Functions
An exponential function is a mathematical function of the form f(x) = a^x, where a is a constant greater than zero and not equal to one. Graphing exponential functions can help us visualize and understand how they behave.
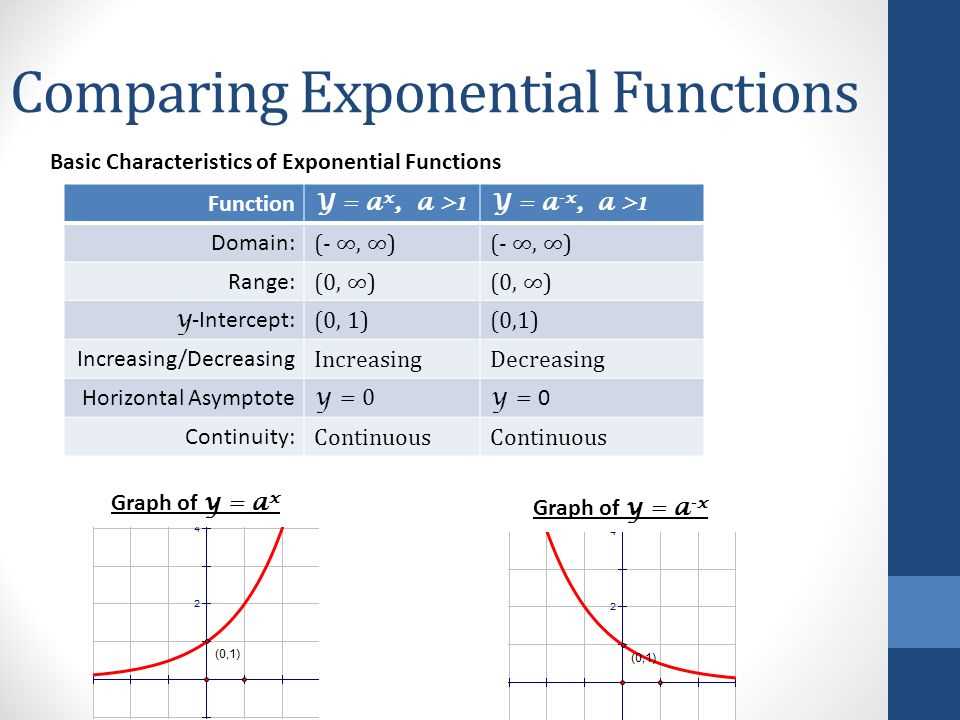
When graphing exponential functions, it’s important to remember a few key points. First, the domain of an exponential function is all real numbers. This means we can input any value of x and calculate the corresponding value of f(x).
The graph of an exponential function can take on different shapes depending on the value of a. If a is greater than 1, the graph will be increasing and approach positive infinity as x approaches positive or negative infinity. If a is between 0 and 1, the graph will be decreasing and approach zero as x approaches positive or negative infinity.
An important feature to note on the graph of an exponential function is the y-intercept. For any exponential function f(x) = a^x, the y-intercept is always (0, 1), since any number raised to the power of zero is equal to one.
Another key feature to observe is the end behavior of the graph. As x approaches positive or negative infinity, the graph will approach zero if a is between 0 and 1, or it will approach positive infinity if a is greater than 1.
When graphing exponential functions, it’s helpful to plot a few points and connect them with a smooth curve. This will give us an idea of how the function behaves between the plotted points. Additionally, it’s important to label the axis and indicate the y-intercept and any other key points.
Overall, graphing exponential functions allows us to visualize their behavior and understand how they change as x increases or decreases. It’s a useful tool in analyzing and solving problems involving exponential growth or decay.
Applications of Exponential Functions
Exponential functions have a wide range of applications in various fields, including finance, biology, and physics. These functions describe processes that grow or decay at a constant rate over time, making them useful for modeling phenomena that exhibit exponential growth or decay.
Finance: Exponential functions are frequently used in finance to model compound interest and investment growth. For example, the compound interest formula A = P(1 + r/n)^(nt) can be rewritten as an exponential function, where P is the principal amount, r is the annual interest rate, n is the number of times interest is compounded per year, and t is the number of years. This allows investors to calculate the future value of their investments and make informed decisions.
Biology: Exponential growth can be observed in population dynamics and the spread of infectious diseases. In population biology, exponential growth occurs when individuals reproduce at a constant rate and there are no limiting factors. Exponential functions can be used to model population growth over time and predict future population sizes. Similarly, in epidemiology, exponential functions can be used to model the spread of diseases, such as COVID-19, and estimate the number of infected individuals.
Physics: Exponential decay is often seen in radioactive decay and natural processes. The decay of radioactive isotopes follows an exponential decay function, where the amount of radioactive material decreases at a constant rate over time. This property is used in radiocarbon dating and other dating methods to determine the age of artifacts and geological materials. Additionally, exponential functions are used to model other physical phenomena, such as the attenuation of signals in communication systems or the decay of electromagnetic fields.
Overall, exponential functions play a crucial role in understanding and modeling various processes in finance, biology, and physics. Their ability to describe growth and decay at a constant rate makes them valuable tools for predicting future outcomes and making informed decisions.
Common Mistakes to Avoid
When working with exponents and exponential functions, it’s important to be aware of some common mistakes that students often make. By avoiding these mistakes, you can improve your understanding of the topic and achieve better results in your exams and assignments. Here are a few common mistakes to watch out for:
Forgetting the Rules of Exponents
One common mistake is forgetting the rules of exponents. These rules govern how exponents can be manipulated and combined. For example, the rule that states that multiplying two numbers with the same base but different exponents results in adding the exponents. Forgetting or misunderstanding these rules can lead to incorrect calculations and answers.
Confusing Exponential Functions with Linear Functions
Another mistake is confusing exponential functions with linear functions. Exponential functions have a specific form where the independent variable is the exponent. Linear functions, on the other hand, have a constant rate of change. Mixing up these two types of functions can lead to errors in graphing and solving equations.
Misinterpreting Negative Exponents
Negative exponents can be confusing for some students. It’s important to remember that a negative exponent indicates the reciprocal of the base raised to the positive exponent. For example, x^-2 is equal to 1/x^2. Misinterpreting negative exponents can result in incorrect calculations and solutions.
Not Simplifying Exponential Expressions

Many problems involving exponents require simplifying the expressions before proceeding with calculations. Failing to simplify an expression can lead to more complex calculations and potential errors along the way. Always look for opportunities to simplify exponential expressions and make your work more manageable.
Not Checking the Domain of Exponential Functions

Exponential functions often have restrictions on their domain. For example, the base cannot be negative if the exponent is not an integer. Not checking the domain of an exponential function can result in solutions that are not valid or do not make sense in the context of the problem. Always double-check the domain of exponential functions to ensure that your solutions are valid.