
Understanding and mastering the concepts of polygons and quadrilaterals is essential in the study of geometry. In this unit, we have covered various topics related to these geometric shapes, including their properties, classifications, and measurements. Now, it’s time to assess your knowledge and skills with the unit 8 test.
The unit 8 test on polygons and quadrilaterals will allow you to demonstrate your understanding of different types of polygons, such as triangles, quadrilaterals, and polygons with more than four sides. You will be required to identify the properties of these shapes and determine their classification based on their attributes.
Moreover, the test will assess your ability to calculate the measurements of polygons, including their angles and side lengths. You will be challenged to apply formulas and theorems to find missing values and solve various problems. It is important to have a strong grasp of the concepts covered in this unit to tackle these test questions effectively.
This answer key provides the correct solutions and explanations for each question in the unit 8 test on polygons and quadrilaterals. It will serve as a valuable resource for you to review your answers, identify any mistakes or misconceptions, and further deepen your understanding of the topic. Use this answer key as a tool for self-assessment and improvement as you continue your journey in geometry.
Understanding Polygons and Quadrilaterals

Polygons and quadrilaterals are fundamental concepts in geometry that describe different types of shapes and their properties. A polygon is a closed figure formed by straight lines, while a quadrilateral is a specific type of polygon that has four sides. By understanding these shapes, we can classify and analyze various geometric figures and solve problems involving their measurements and relationships.
A polygon is characterized by the number of sides it has, and each side is a line segment connecting two consecutive vertices or corners. Some examples of polygons include triangles (3 sides), quadrilaterals (4 sides), pentagons (5 sides), hexagons (6 sides), and so on. The sum of the interior angles of any polygon can be found using the formula (n – 2) × 180 degrees, where n represents the number of sides.
A quadrilateral is a four-sided polygon that can have different types of angles and side lengths. Some common types of quadrilaterals include squares, rectangles, parallelograms, trapezoids, and rhombuses. Each type has its own set of properties and characteristics. For example, a square has four congruent sides and four right angles, while a parallelogram has opposite sides that are parallel and congruent.
Understanding polygons and quadrilaterals is important in various fields, including architecture, engineering, and design. By knowing the properties and relationships of these shapes, we can accurately measure and construct objects, create geometric models, and solve real-world problems. So whether you’re calculating the area of a triangular roof or designing a floor plan with different quadrilaterals, a solid understanding of these concepts will be invaluable.
What are polygons and quadrilaterals?

Polygons and quadrilaterals are geometric shapes that are made up of straight lines. They are an important part of geometry and are studied extensively in mathematics. A polygon is a closed figure with three or more sides, while a quadrilateral is a polygon with four sides. Both polygons and quadrilaterals have various properties and characteristics that make them unique and interesting.
Polygons and quadrilaterals can be divided into different categories based on the lengths of their sides and the measures of their angles. For example, a regular polygon has all sides and angles that are equal, while an irregular polygon does not. Quadrilaterals can also be classified based on their properties, such as being a rectangle, square, or parallelogram.
One important property of polygons and quadrilaterals is their interior angles. The sum of the interior angles of a polygon is determined by its number of sides. For example, a triangle has interior angles that add up to 180 degrees, while a quadrilateral has interior angles that add up to 360 degrees. This property allows mathematicians to find missing angles and solve problems involving polygons and quadrilaterals.
Overall, polygons and quadrilaterals are fundamental shapes in geometry. They are used in various real-life situations, such as in architecture, engineering, and art. Understanding their properties and characteristics is important for solving problems and making accurate measurements in these fields and in mathematics as a whole.
Identifying Polygons and Quadrilaterals
Polygons and quadrilaterals are two-dimensional shapes that are made up of straight lines called sides. Each side of a polygon or a quadrilateral connects to another side at a vertex, creating a closed shape. By identifying the characteristics of a shape, we can determine whether it is a polygon or a quadrilateral.
A polygon is a shape that has at least three sides and three angles. The number of sides in a polygon can vary, and each side should be straight. The angles inside a polygon should also be less than 180 degrees. Examples of polygons include triangles, quadrilaterals, pentagons, hexagons, and so on.
A quadrilateral, as the name suggests, is a polygon that has four sides. The sides of a quadrilateral can be of different lengths, and the angles between the sides can also vary. There are different types of quadrilaterals such as squares, rectangles, parallelograms, trapezoids, and rhombuses. Each type of quadrilateral has its own set of defining characteristics.
To identify whether a shape is a polygon or a quadrilateral, we can count the number of sides. If the shape has at least three sides, it is a polygon. If the shape has four sides, it is a quadrilateral. Then, we can further analyze the shape to determine its specific type, based on its characteristics such as angles and side lengths.
Key Points:
- A polygon is a shape with at least three straight sides and angles.
- A quadrilateral is a type of polygon with four sides.
- Quadrilaterals can have different types such as squares, rectangles, parallelograms, trapezoids, and rhombuses.
- By analyzing the characteristics of a shape, we can identify whether it is a polygon or a quadrilateral.
Types of polygons and their properties
A polygon is a closed figure in a plane formed by connecting line segments. There are different types of polygons, each with its own unique properties and characteristics. Here are some of the most common types of polygons:
- Triangle: A triangle is a polygon with three sides. It is the simplest polygon and has three vertices and three angles. The sum of the interior angles of a triangle is always 180 degrees.
- Quadrilateral: A quadrilateral is a polygon with four sides. It has four vertices and four angles. Examples of quadrilaterals include squares, rectangles, parallelograms, and trapezoids.
- Pentagon: A pentagon is a polygon with five sides. It has five vertices and five angles. The sum of the interior angles of a pentagon is 540 degrees.
- Hexagon: A hexagon is a polygon with six sides. It has six vertices and six angles. The sum of the interior angles of a hexagon is 720 degrees.
- Octagon: An octagon is a polygon with eight sides. It has eight vertices and eight angles. The sum of the interior angles of an octagon is 1080 degrees.
In addition to these basic polygons, there are also regular and irregular polygons. A regular polygon has all sides and angles equal in measure, while an irregular polygon has sides and/or angles of different lengths or measures.
Understanding the properties of different types of polygons is essential in geometry. It allows us to identify and classify polygons based on their characteristics, and helps us solve problems involving angles, sides, and symmetry.
Characteristics of quadrilaterals
A quadrilateral is a polygon with four sides. There are several different types of quadrilaterals, each with its own unique characteristics.
One type of quadrilateral is a parallelogram. A parallelogram has two pairs of parallel sides. This means that opposite sides are equal in length and parallel to each other. Additionally, the opposite angles of a parallelogram are also equal. These characteristics make a parallelogram a special type of quadrilateral.
Another type of quadrilateral is a rectangle. A rectangle is a parallelogram with four right angles. This means that all four angles of a rectangle are equal to 90 degrees. In addition to having four right angles, a rectangle also has opposite sides that are equal in length. These characteristics make a rectangle a special type of parallelogram.
A square is another type of quadrilateral. A square is a special type of rectangle where all four sides are equal in length. In addition to having four equal sides, a square also has four right angles. These characteristics make a square a special type of rectangle and parallelogram.
A trapezoid is a quadrilateral that has one pair of parallel sides. The other two sides of a trapezoid are not parallel, which differentiates it from a parallelogram. In a trapezoid, the non-parallel sides are known as the legs, while the parallel sides are known as the bases.
These are just a few examples of the different characteristics of quadrilaterals. Each type of quadrilateral has its own unique properties, which makes studying and categorizing them an interesting part of geometry.
Working with Angles in Polygons and Quadrilaterals

Angles are an important concept in geometry, and they play a crucial role in understanding polygons and quadrilaterals. A polygon is a closed figure with straight sides, and a quadrilateral is a polygon with four sides. When working with angles in polygons and quadrilaterals, it is important to understand the properties and relationships between different angles within these shapes.
One key concept is the sum of the interior angles in a polygon. The sum of the interior angles in a polygon with n sides can be found using the formula (n-2) * 180 degrees. For example, a triangle has three sides, so the sum of its interior angles is (3-2) * 180 = 180 degrees. Similarly, a quadrilateral has four sides, so the sum of its interior angles is (4-2) * 180 = 360 degrees.
Another important concept is the properties of angles in quadrilaterals. In a parallelogram, opposite angles are equal, meaning that they have the same measure. In a rectangle, all angles are right angles, or 90 degrees. In a rhombus, all angles are equal, but they are not necessarily right angles. These properties can be applied to solve problems involving angles in quadrilaterals.
Working with angles in polygons and quadrilaterals requires a strong understanding of angle relationships and geometric properties. By familiarizing ourselves with these concepts, we can confidently solve problems and analyze shapes with ease.
Measuring angles in polygons
In geometry, a polygon is a closed figure made up of straight line segments that are joined together. One important aspect of studying polygons is measuring the angles within them. An angle is the amount of rotation needed to bring one line segment into coincidence with another.
When measuring angles in polygons, it is important to remember that the sum of the interior angles of any polygon is always equal to (n-2) × 180 degrees, where n is the number of sides or vertices in the polygon. This is known as the polygon angle sum theorem.
For example, let’s consider a triangle, which is a polygon with three sides. According to the polygon angle sum theorem, the sum of the interior angles of a triangle is equal to (3-2) × 180 degrees, which is 180 degrees. Therefore, each interior angle of a triangle measures 60 degrees.
Measuring angles in polygons involves using tools such as protractors. A protractor is a semicircular tool with markings that allows for precise angle measurement. To measure an angle, the vertex of the angle is aligned with the center of the protractor, and the sides of the angle are extended along the protractor’s scale. The intersection point of the angle sides with the protractor’s scale indicates the measurement of the angle in degrees.
Understanding how to measure angles in polygons is crucial in geometry, as it helps solve problems related to angles, such as finding unknown angles or determining the congruence of angles in different polygons.
Angle properties of quadrilaterals
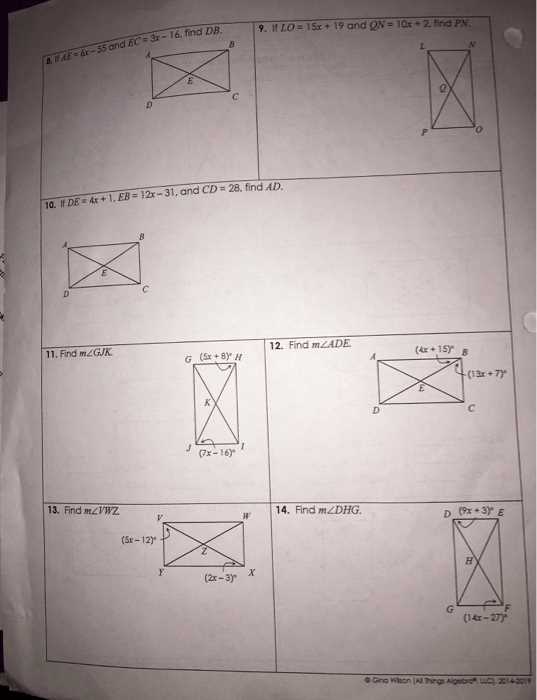
Quadrilaterals are polygons with four sides and four angles. Each type of quadrilateral has its own set of properties and characteristics. Understanding the angle properties of quadrilaterals is essential in geometry, as it helps us determine the relationships between the angles and sides of these shapes.
There are several types of quadrilaterals, including parallelograms, rectangles, squares, rhombuses, trapezoids, and kites. Each type has unique properties, but they all share certain angle properties.
- Sum of angles: The sum of the interior angles of any quadrilateral is always 360 degrees.
- Opposite angles: In a quadrilateral, opposite angles are congruent, meaning they have equal measures.
- Adjacent angles: Adjacent angles in a quadrilateral add up to 180 degrees.
- Diagonals: The diagonals of a quadrilateral intersect each other at a point called the centroid, and they divide the quadrilateral into two pairs of congruent triangles.
By understanding and applying these angle properties, we can solve various problems involving quadrilaterals, such as finding the measures of missing angles, proving the congruence of quadrilaterals, and determining the type of quadrilateral based on its angle properties.
Calculating Perimeter and Area of Polygons and Quadrilaterals
A polygon is a closed shape made up of straight sides. One important aspect of polygons is calculating their perimeter, which is the distance around the outside of the shape. To find the perimeter, you add up the lengths of all the sides. For example, if you have a triangle with sides measuring 3 cm, 4 cm, and 5 cm, the perimeter would be 3 + 4 + 5 = 12 cm.
In addition to perimeter, another important measurement for polygons is the area. The area of a polygon represents the amount of space inside the shape. To calculate the area of a polygon, you need to know the length of the sides and the height of the polygon. The formula for finding the area of a triangle is usually base x height divided by 2. For example, if a triangle has a base of 6 cm and a height of 4 cm, the area would be (6 x 4) / 2 = 12 cm².
Quadrilaterals, a specific type of polygon with four sides, also have their own formulas for calculating perimeter and area. The perimeter of a quadrilateral is found by adding up the lengths of all four sides. To find the area, different formulas can be used depending on the specific type of quadrilateral. For example, the area of a rectangle can be found by multiplying the length and width, while the area of a square is found by squaring one of the sides.
Overall, calculating the perimeter and area of polygons and quadrilaterals involves understanding the formulas specific to each shape. By applying these formulas correctly, you can determine the measurements and better understand the characteristics of these geometric shapes.