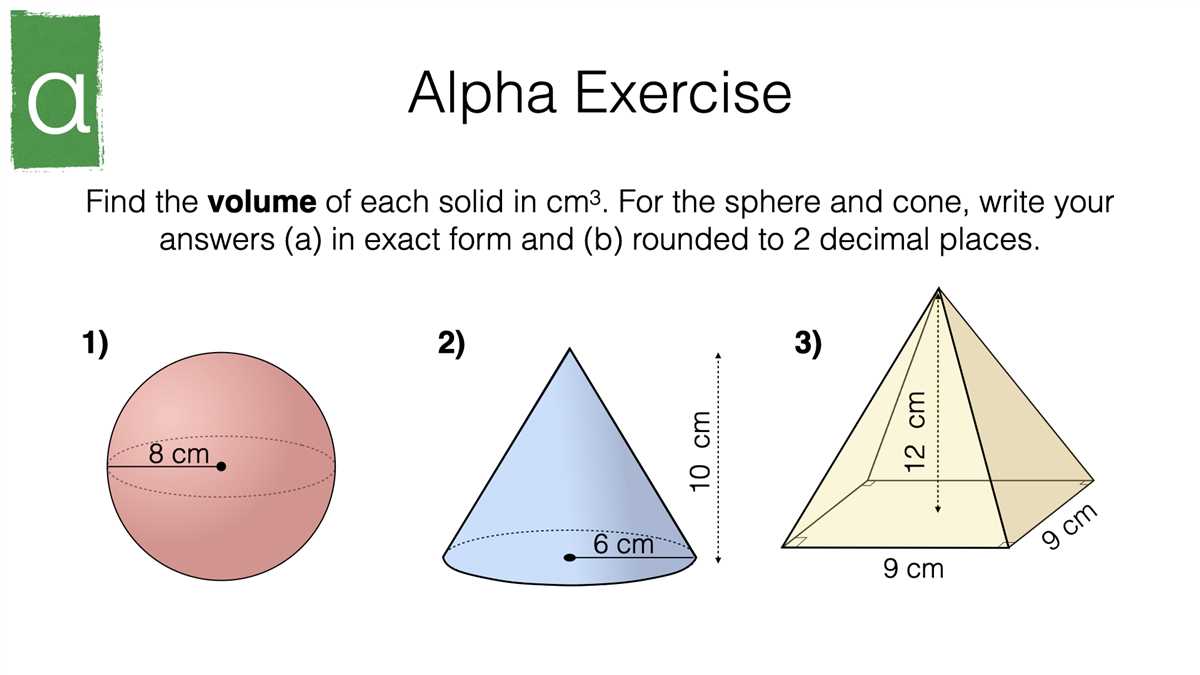
In geometry, the volume of a solid is a fundamental concept that measures the amount of space occupied by the object. One of the key shapes we often encounter is a cone, which is a three-dimensional object with a circular base and a pointed top. Understanding how to calculate the volume of a cone is essential for solving various geometry problems and real-life applications.
To find the volume of a cone, we need to know the radius of the base and the height of the cone. The formula for the volume of a cone is V = 1/3 * π * r^2 * h, where V represents the volume, π is a mathematical constant approximately equal to 3.14, r is the radius of the base, and h is the height of the cone.
In this homework, students were tasked with calculating the volume of different cones using the given measurements. The answers key provides the correct solutions to the problems and serves as a guide for students to check their work and understand the steps involved in finding the volume of cones.
Unit Volume Homework 2 Volume of Cones Answers Key

In this homework assignment, we will be exploring the concept of volume in the context of cones. A cone is a three-dimensional shape that has a circular base and tapers to a single point called the apex. To find the volume of a cone, we can use the formula V = (1/3)πr^2h, where V is the volume, π is a mathematical constant approximately equal to 3.14159, r is the radius of the base, and h is the height of the cone.
Let’s go through some example problems and find the volume of cones using the given measurements. For example, if we have a cone with a radius of 5 units and a height of 8 units, we can plug these values into the volume formula to get V = (1/3)π(5^2)(8) ≈ 83.78 cubic units. This means that the volume of the cone is approximately 83.78 cubic units.
Now, let’s look at another example. Suppose we have a cone with a radius of 3 units and a height of 10 units. Using the volume formula, we can calculate V = (1/3)π(3^2)(10) ≈ 94.25 cubic units. Therefore, the volume of this cone is approximately 94.25 cubic units.
By solving similar problems using the volume formula for cones, you can improve your understanding of the concept and gain confidence in calculating the volume of different shapes. Remember to plug in the given measurements correctly and use the correct formula to obtain accurate answers. Keep practicing and exploring more examples to sharpen your skills in finding the volume of cones.
Definition and Formula of Cone Volume
A cone is a three-dimensional geometric shape that has a circular base and tapers to a single point called the apex. It can be visualized as a triangular pyramid with a circular base. The volume of a cone is the amount of space enclosed by the cone.
Formula: The formula to calculate the volume of a cone is V = (1/3)πr^2h, where V represents the volume, π represents the mathematical constant pi (approximately 3.14159), r represents the radius of the base of the cone, and h represents the height of the cone.
To calculate the volume of a cone, one needs to know the radius of the cone’s base and its height. The radius is the distance from the center of the base to any point on the circumference of the base, while the height is the distance from the apex to the base.
Example: Let’s say we have a cone with a radius of 4 centimeters and a height of 6 centimeters. Substituting these values into the formula, we get V = (1/3)π(4^2)(6) = 32π cm^3. Therefore, the volume of the cone is approximately 100.53 cubic centimeters.
The formula for finding the volume of a cone can be derived by considering the cone as a series of infinitesimally thin disks stacked on top of each other. By integrating the area of each disk over the height of the cone, we can obtain the formula mentioned above.
Example Calculation of Cone Volume
In order to calculate the volume of a cone, we need to know the radius of the base and the height of the cone. Let’s consider an example:
Example: Find the volume of a cone with a radius of 4 cm and a height of 6 cm.
To calculate the volume of the cone, we can use the formula: V = (1/3) * π * r^2 * h, where V is the volume, π is a mathematical constant approximately equal to 3.14, r is the radius of the base, and h is the height of the cone.
Using the given values, we can substitute them into the formula:
- Radius (r) = 4 cm
- Height (h) = 6 cm
- π (pi) = 3.14
Plugging these values into the formula, we get:
V = (1/3) * 3.14 * 4^2 * 6
Simplifying the equation, we have:
V = (1/3) * 3.14 * 16 * 6
V = (1/3) * 3.14 * 96
V ≈ 100.53
Therefore, the volume of the cone with a radius of 4 cm and a height of 6 cm is approximately 100.53 cubic centimeters.
In conclusion, calculating the volume of a cone requires knowing the radius of the base and the height of the cone, and using the formula V = (1/3) * π * r^2 * h. By substituting the given values into the formula, we can determine the volume of the cone.
Application of Cone Volume in Real Life
The volume of a cone is a concept that finds numerous applications in real life. One of the most common applications is in the field of construction and architecture. Conical shapes often appear in architectural structures such as domes, roofs, and towers. By understanding the volume of a cone, architects and engineers can accurately calculate the amount of material needed to construct these complex structures. This ensures efficient use of resources and helps in cost estimation.
Another area where cone volume is applied is in the design and manufacturing of containers. Many containers, such as ice cream cones, traffic cones, and party hats, have a conical shape. Knowledge of cone volume is crucial for determining the capacity or filling level of these containers. It helps in ensuring that the proper amount of product or material can be stored or transported in these containers.
Additionally, cone volume is used in various scientific and engineering fields. For example, in the field of fluid dynamics, the volume of a cone plays a role in analyzing the flow of liquids or gases through conical pipes or nozzles. The volume calculations help in predicting fluid behavior, pressure drop, and flow rate. Similarly, in the field of acoustics, cone volumes are used to design loudspeakers and other audio devices. The calculations help in optimizing the sound output and frequency response of these devices.
In conclusion, the concept of cone volume has practical applications in different areas of life, including construction, manufacturing, and various scientific and engineering fields. Understanding the volume of a cone enables professionals in these fields to make accurate calculations, design efficient structures, and optimize the performance of various devices. It is an essential concept that finds widespread use in real-life scenarios.
Common Mistakes and Troubleshooting in Cone Volume Calculations
Calculating the volume of a cone can sometimes be tricky, and it’s not uncommon to make mistakes along the way. Here are some common errors and troubleshooting tips to help you navigate through cone volume calculations.
Using the wrong formula
One of the most common mistakes is using the wrong formula to calculate the volume of a cone. The correct formula is V = (1/3)πr^2h, where V is the volume, r is the radius of the base, and h is the height of the cone. Make sure you understand the correct formula and double-check your calculations to avoid this mistake.
Incorrectly measuring the radius or height

Another common mistake is incorrectly measuring the radius or height of the cone. It’s important to measure these values accurately to get an accurate volume calculation. Use appropriate tools, such as a ruler or measuring tape, and be careful when taking measurements to avoid errors.
Forgetting to convert units
When working with units, it’s essential to convert them appropriately to ensure consistent calculations. For example, if the radius is given in inches and the height in centimeters, you need to convert one of them to match the units of the other. Not converting units can lead to incorrect volume calculations, so always double-check and convert if necessary.
Confusing diameter with radius
Another mistake that can occur is confusing the diameter with the radius of the cone’s base. The radius is half the diameter, so make sure you’re using the correct value in the formula for the volume calculation. If you accidentally use the diameter instead of the radius, the result will be incorrect.
- Always double-check and verify the formula you’re using.
- Be precise when measuring the radius and height of the cone.
- Convert units if necessary to ensure consistency.
- Don’t confuse the diameter with the radius.
By being aware of these common mistakes and following the troubleshooting tips, you can enhance the accuracy of your cone volume calculations. Practice and repetition will also help you become more proficient in solving cone volume problems.
Tips and Tricks for Solving Cone Volume Problems
When it comes to solving volume problems for cones, there are several useful strategies and tips to keep in mind. Understanding these techniques can greatly simplify the process and help you arrive at the correct answers efficiently. Here are some key tips and tricks to remember:
1. Use the formula

The most basic and fundamental tip for solving cone volume problems is to use the formula for the volume of a cone: V = 1/3 * π * r^2 * h. This formula connects the radius (r) and height (h) of the cone to its volume (V), and it is the starting point for most cone volume calculations.
2. Pay attention to units
When working with volume problems, it is crucial to pay close attention to the units involved. Make sure that all measurements are in the same unit (e.g., centimeters or inches) before plugging them into the formula. Additionally, remember to include the appropriate unit in your final answer.
3. Know when to use the slant height
In some cone volume problems, you may be given the slant height (l) instead of the height (h). Remember that in such cases, you can still use the formula mentioned earlier by substituting the slant height for the height. This can be particularly useful when the slant height is easier to measure or work with.
4. Simplify fractions
Volume calculations often involve fractions, especially when dealing with the 1/3 factor in the formula. To simplify calculations, consider canceling out common factors, multiplying before dividing, or reducing fractions whenever possible. This can save time and make calculations less complex.
5. Round to the nearest decimal
Volume measurements are typically expressed in cubic units, such as cubic centimeters or cubic inches. When rounding your answer, be sure to follow the appropriate rules for decimal places or significant figures. Usually, it is best to round to the nearest decimal place unless otherwise specified or instructed.
By keeping these tips and tricks in mind, you can approach cone volume problems with confidence and solve them effectively. Remember to practice and apply these strategies to gain a deeper understanding of how to calculate cone volumes accurately.