
If you’re looking for answers to a velocity-time graph worksheet, you’ve come to the right place. Understanding and interpreting velocity-time graphs is an important skill in physics and can help you analyze an object’s motion and its changes over time. By carefully analyzing the graph and calculating the slope, you can determine the object’s velocity at specific points and gain insight into its acceleration.
In this article, we will provide answers to a velocity-time graph worksheet, explaining step-by-step how to interpret and analyze the graph. We will cover topics such as calculating velocity from the slope of the graph, identifying constant velocity, acceleration, and determining the direction of motion. By the end of this article, you will have a clear understanding of how to analyze velocity-time graphs and be able to confidently answer questions on your worksheet.
Each question on the worksheet will be accompanied by a velocity-time graph. We will break down the graph into different intervals and provide detailed explanations for each interval. By following along with our answers, you will learn how to identify key features on the graph and interpret the object’s motion accordingly. We will also provide tips and tricks for completing the worksheet efficiently and accurately.
Understanding Velocity-Time Graphs
A velocity-time graph is a graphical representation of the relationship between an object’s velocity and time. It provides a visual representation of how an object’s velocity changes over a period of time. By analyzing and interpreting velocity-time graphs, we can gain important insights into an object’s motion and understand its acceleration, deceleration, and any changes in direction.
Interpreting the graph: In a velocity-time graph, the horizontal axis represents time, while the vertical axis represents velocity. The slope of the graph at any given point indicates the rate at which the velocity is changing. A positive slope indicates an increase in velocity, while a negative slope indicates a decrease in velocity. A horizontal line represents constant velocity, while a curved line represents changing velocity.
Understanding acceleration: Acceleration is represented by the steepness of the graph. A steeper slope indicates a higher acceleration, while a shallower slope indicates a lower acceleration. If the graph shows a straight line with a constant slope, it indicates a constant acceleration. If the graph is a curved line, it indicates a changing acceleration.
Identifying significant points: Certain points on the graph have specific meanings. For example, the point where the graph intersects the horizontal axis represents the time at which the object starts or stops moving. The steeper the slope of the graph, the faster the object is moving. The area under the graph represents the displacement of the object.
Comparing objects: Comparing velocity-time graphs of different objects can provide insights into their relative motion. For example, if one object’s graph is steeper than another object’s graph, it indicates that the first object has a higher acceleration or is changing its velocity at a faster rate. By analyzing these graphs, we can understand how different objects move and how their velocities change over time.
Velocity-time graphs are a powerful tool in analyzing and understanding the motion of objects. By interpreting the graph and identifying key points, we can gain valuable insights into an object’s acceleration, deceleration, and changes in direction. By comparing graphs of different objects, we can also understand how their motion differs. With this knowledge, we can make accurate predictions about an object’s future motion and behavior.
What is a velocity-time graph?
A velocity-time graph, also known as a speed-time graph, is a visual representation of an object’s velocity or speed over a period of time. It is a useful tool in understanding and analyzing the motion of objects, as it provides information about an object’s direction, magnitude, and changes in velocity.
The velocity-time graph is plotted with time on the x-axis and velocity on the y-axis. The slope of the graph represents the object’s acceleration, where a steeper slope indicates a higher acceleration. A horizontal line on the graph indicates a constant velocity, while a curve or a changing slope represents a changing velocity.
By studying the shape and characteristics of a velocity-time graph, we can determine various aspects of an object’s motion. For example, a positive slope indicates motion in the positive direction, while a negative slope represents motion in the negative direction.
Additionally, the area under the graph represents the displacement or distance traveled by the object. The magnitude of the area can tell us about the overall displacement of the object, while the direction of the area can indicate whether the object is moving forward or backward.
To interpret a velocity-time graph accurately, it is important to understand the key concepts of velocity and time. Velocity is the rate of change of displacement with respect to time, while time is the duration or interval during which the motion occurs. By analyzing the velocity-time graph, we can gain insights into the motion of objects and further investigate the underlying principles of physics.
Interpreting Velocity-Time Graphs

Velocity-time graphs are graphical representations of an object’s velocity as it changes over time. These graphs are an important tool in understanding the motion of an object and can provide valuable information about its speed, direction, and acceleration. By analyzing the shape and slope of the graph, we can interpret various aspects of an object’s motion.
1. Constant Velocity: When a velocity-time graph shows a straight, horizontal line, it indicates that the object is moving at a constant velocity. The slope of the line represents the object’s speed, and the fact that the line is horizontal indicates that its velocity is not changing with time.
2. Uniform Acceleration: An upward sloping line on a velocity-time graph represents uniform acceleration. The steeper the slope, the greater the acceleration. The slope of the line can also be used to calculate the object’s acceleration, as it represents the rate at which the velocity is changing with time.
3. Changing Direction: A change in direction is indicated by a change in the sign of the velocity on the graph. For example, if the velocity changes from positive to negative, it means the object is reversing its direction. The point on the graph where this change occurs is called the point of reversal.
4. Zero Velocity: When the velocity-time graph crosses the x-axis, it shows that the object has zero velocity at that point in time. This can occur when the object is momentarily at rest, or when it changes direction and its velocity becomes zero before reversing.
To draw meaningful conclusions from a velocity-time graph, it is important to carefully analyze its shape, slope, and any points of inflection or reversal. By doing so, we can gain a deeper understanding of an object’s motion and its interaction with its surroundings.
How to read and interpret a velocity-time graph
A velocity-time graph, also known as a speed-time graph, provides valuable information about the motion of an object. By analyzing the graph, you can determine various aspects of the object’s motion, such as its acceleration, velocity, and displacement. To interpret a velocity-time graph, follow these steps:
1. Understand the axes:
The velocity-time graph has the velocity (or speed) of the object plotted along the y-axis and time plotted along the x-axis. Make sure you understand the units being used on each axis, as this will affect how you interpret the graph.
2. Analyze the slope:
The slope of the velocity-time graph represents the acceleration of the object. If the graph has a constant positive slope, it means the object is accelerating in a positive direction. If the slope is constant and negative, the object is accelerating in a negative direction. A horizontal line indicates that the object is traveling at a constant velocity.
3. Determine the velocity:
The velocity of the object at any given point on the graph can be found by looking at the y-coordinate. Positive values represent forward motion, while negative values represent backward motion. The steeper the slope, the greater the velocity of the object.
4. Calculate the displacement:
To determine the displacement of the object, you need to find the area under the velocity-time graph. This can be done by calculating the area of the individual rectangles or triangles formed by the graph. The displacement can be positive or negative, depending on the direction of motion.
5. Look for key points:
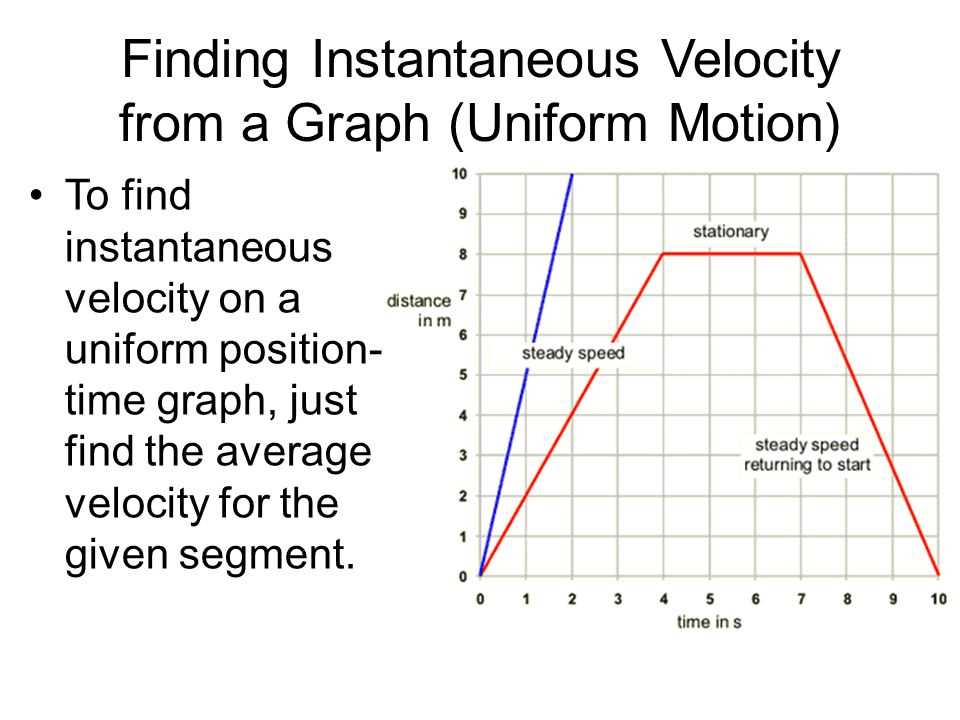
Identify any significant points on the graph, such as peaks, troughs, or inflection points. These points can provide important information about the object’s motion, such as when it changes direction or reaches maximum acceleration.
By following these steps, you can read and interpret a velocity-time graph to gain insights into the motion of an object. It is essential to understand the graph’s elements, such as the axes, slope, velocity, and displacement, to fully comprehend the object’s motion.
Calculating Velocity from a Graph
The velocity-time graph is a graphical representation of an object’s velocity over time. It provides valuable information about the object’s motion, including its speed and direction. Understanding how to calculate velocity from a graph is crucial in analyzing and interpreting the data.
One way to calculate velocity from a graph is by determining the slope of the line. The slope represents the rate of change in velocity over time. It is calculated by dividing the change in the y-axis (velocity) by the change in the x-axis (time). A steeper slope indicates a higher velocity, while a flatter slope represents a lower velocity. Additionally, a positive slope indicates motion in the positive direction, while a negative slope indicates motion in the negative direction.
Another method to calculate velocity is by finding the area under the velocity-time graph. When an object is moving at a constant velocity, the area under the graph represents the distance traveled. To calculate velocity in this case, divide the distance traveled by the time taken. If the graph is not a straight line and the velocity changes, then the area under the graph needs to be separated into different sections, and the velocity can be calculated by dividing the distance traveled in each section by the time taken.
Overall, calculating velocity from a graph involves analyzing the slope, interpreting its meaning in terms of speed and direction, and determining the area under the graph to calculate the distance traveled. It is an essential skill in physics and allows for a deeper understanding and analysis of an object’s motion.
How to calculate velocity from a velocity-time graph
A velocity-time graph is a graphical representation of an object’s velocity as a function of time. By analyzing this graph, we can determine the object’s velocity at any given point in time. To calculate velocity from a velocity-time graph, we need to understand the concept of slope or gradient.
The slope of a line on a velocity-time graph represents the object’s acceleration. The steeper the slope, the greater the acceleration. To calculate the velocity from a velocity-time graph, we need to calculate the slope of the line segment that represents the desired time interval.
To calculate the slope, we need to find the rise and run of the line segment. The rise is the change in the vertical axis (velocity) and the run is the change in the horizontal axis (time). By dividing the rise by the run, we can determine the velocity at that specific time interval.
For example, let’s say we have a velocity-time graph where the rise is 10 m/s and the run is 2 seconds. Dividing the rise by the run, we get a velocity of 5 m/s. This means that the object’s velocity at that specific time interval is 5 m/s.
It is important to note that when calculating velocity from a velocity-time graph, we are finding the average velocity over a specific time interval. To find the instantaneous velocity at a specific point in time, we would need to take the limit as the time interval approaches zero.
Identifying Acceleration on a Velocity-Time Graph
In physics, velocity-time graphs are used to represent the motion of an object over a period of time. These graphs plot the velocity of the object on the y-axis and the time on the x-axis. By analyzing these graphs, we can determine various aspects of the object’s motion, such as acceleration.
Acceleration is defined as the rate of change of velocity with respect to time. On a velocity-time graph, acceleration can be identified by examining the slope of the graph. If the slope of the graph is positive, it indicates that the object is accelerating in the positive direction. Conversely, if the slope is negative, it means that the object is accelerating in the negative direction or decelerating.
To calculate the acceleration from a velocity-time graph, we can use the equation: acceleration = change in velocity / change in time. This can be done by determining the change in velocity between two points on the graph and dividing it by the corresponding change in time.
Alternatively, if the velocity-time graph is a straight line, the acceleration can be calculated by dividing the change in velocity by the total time taken. The magnitude of the acceleration can also be determined by calculating the slope of the straight line.
- If the velocity-time graph is a straight line with a positive slope, it indicates a constant acceleration in the positive direction.
- If the velocity-time graph is a straight line with a negative slope, it indicates a constant acceleration in the negative direction or deceleration.
- If the velocity-time graph is a curve, the acceleration can be determined by finding the slope of the tangent line at a specific point on the curve.
By understanding how to identify acceleration on a velocity-time graph, we can analyze and interpret the motion of objects in real-world scenarios. This knowledge is essential in fields such as physics, engineering, and transportation.