
If you are studying geometry or preparing for a math test, you might come across various problems related to finding the volume of a cone. To help you practice this concept, a volume of cone worksheet with answers in PDF format can be a great resource. This worksheet provides a series of exercises that will test your understanding and calculation skills when it comes to finding the volume of cones. By engaging with these problems, you can reinforce your knowledge of the formula and gain confidence in solving similar problems on your own.
The volume of a cone is a measurement of the amount of space inside the cone. It is an important concept in geometry and can be calculated using the formula V = (1/3)πr^2h, where V represents the volume, r is the radius of the base of the cone, and h is the height of the cone. By applying this formula to different cone shapes and dimensions, you can deepen your understanding of how the volume of a cone is influenced by its dimensions. The volume of cone worksheet with answers in PDF format will provide you with a range of problems, allowing you to practice applying the formula and working with different cone variations.
Working through a volume of cone worksheet with answers can be beneficial in several ways. It helps you develop problem-solving skills, as you need to analyze the given information, manipulate the formula, and perform the necessary calculations. Additionally, practicing with various problems enhances your fluency in calculating the volume of different cones, increasing your confidence in solving similar problems independently. Moreover, by checking the answers provided in the worksheet, you can assess your progress and identify any areas that require additional practice or review. This enables you to track your improvement and focus your efforts on areas that need further attention.
Volume of Cone Worksheet with Answers PDF: Everything You Need to Know
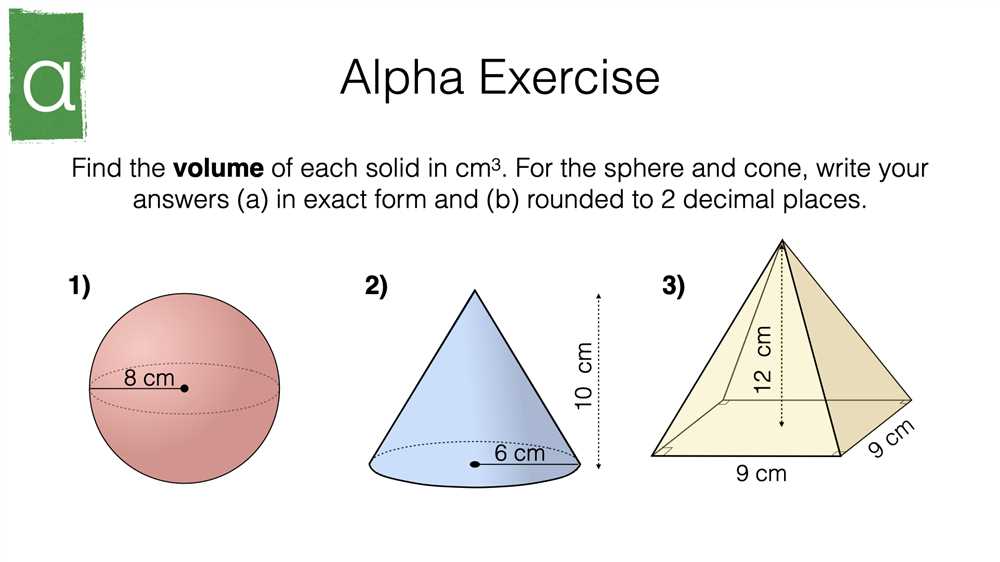
If you are studying geometry and need to practice calculating the volume of cones, a volume of cone worksheet with answers in PDF format can be a valuable tool. This type of worksheet provides a series of cone-shaped figures with different dimensions, and challenges you to solve for their respective volumes. By working through these problems, you can improve your understanding of the cone volume formula and gain confidence in your ability to solve similar problems in the future.
The cone volume formula is derived from the formula for the volume of a cylinder, as cones are a type of three-dimensional shape that can be thought of as a tapered cylinder. The formula for the volume of a cone is V = (1/3)πr^2h, where V represents the volume, π is a mathematical constant (approximately 3.14), r is the radius of the circular base, and h is the height of the cone. By substituting the given values into this formula, you can find the volume of a cone.
A volume of cone worksheet typically provides a set of cone figures, each with different values for the radius and height. The goal is to calculate the volume of each cone. The worksheet may also include an answer key in PDF format, which allows you to check your answers and verify your calculations. This can be especially helpful when practicing on your own, as you can assess your understanding and identify any areas that may require further review.
Working through a volume of cone worksheet with answers PDF can be a valuable way to reinforce your understanding of the cone volume formula and improve your problem-solving skills. By practicing with different cone figures and checking your answers, you can build confidence in your ability to calculate the volume of cones. Remember to carefully review the given values for each cone, substitute them into the formula, and perform accurate calculations to determine the volume. With practice, you will become more proficient in solving volume of cone problems and develop a strong foundation in geometry.
Understanding the Formula for Finding the Volume of a Cone
Calculating the volume of a cone is an essential skill in geometry and is often encountered in various math problems and real-life applications. To find the volume of a cone, we use a specific formula that relates the height and radius of the cone.
The formula for finding the volume of a cone is V = 1/3πr^2h, where V represents the volume, r is the radius of the base of the cone, and h is the height of the cone. This formula is derived using the principles of calculus and can be applied to cones of any size or shape.
In order to use this formula, it is important to understand the different components. The radius is the distance from the center of the base to any point on the edge, while the height is the distance from the tip of the cone to the base, measured along the perpendicular line. It is crucial to measure these dimensions accurately to obtain the correct volume.
Calculating the volume of a cone can be done manually using the formula and a calculator, or it can be found using various online tools and worksheets. These resources provide step-by-step instructions and examples to help students understand the concept and practice applying the formula to different cone problems.
Understanding the formula for finding the volume of a cone is essential for students studying geometry or anyone who encounters cone-related problems in their everyday life. Whether it’s calculating the volume of a traffic cone, a cone-shaped container, or any other cone-like structure, mastering this formula allows for accurate calculations and a deeper comprehension of geometric principles.
Steps to Calculate the Volume of a Cone
To calculate the volume of a cone, you will need to follow a few simple steps. Here is a step-by-step guide to help you calculate the volume of a cone correctly:
- Determine the measurements: First, you need to gather the necessary measurements. You will need the radius of the circular base and the height of the cone. Make sure you have these measurements ready before proceeding.
- Calculate the base area: The base area of a cone can be found using the formula: A = πr^2. Multiply the radius of the base by itself, and then multiply the result by π (pi). This will give you the base area of the cone.
- Calculate the volume: To calculate the volume of the cone, multiply the base area by the height and divide the product by 3. The formula for finding the volume of a cone is V = (1/3)A * h, where A is the base area and h is the height.
- Round the result: Once you have calculated the volume, round the result to the desired number of decimal places. This will give you the final volume of the cone.
By following these steps, you will be able to accurately calculate the volume of any cone. Remember to double-check your measurements and calculations to ensure accuracy. Practice using these steps on different cone examples to improve your understanding of calculating cone volumes.
Practice Problems for Volume of Cone Worksheet
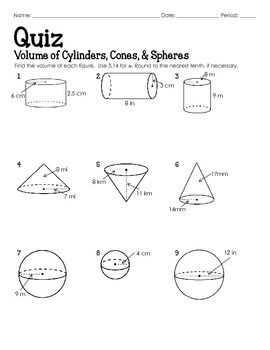
In mathematics, the volume of a cone is calculated using the formula V = 1/3πr²h, where r is the radius of the base and h is the height of the cone. To reinforce your understanding of this concept, the following practice problems will help you calculate the volume of cones.
Problem 1:
A cone has a radius of 4 cm and a height of 8 cm. Calculate its volume.
Solution:
Using the formula V = 1/3πr²h, we can substitute the given values: V = 1/3π(4 cm)²(8 cm) = 1/3π(16 cm²)(8 cm) = 1/3π(128 cm³) = 42.67 cm³ (rounded to two decimal places).
Problem 2:
Find the volume of a cone whose radius is 6 inches and height is 12 inches.
Solution:
Using the formula V = 1/3πr²h, we can substitute the given values: V = 1/3π(6 in)²(12 in) = 1/3π(36 in²)(12 in) = 1/3π(432 in³) = 452.39 in³ (rounded to two decimal places).
Problem 3:
What is the volume of a cone with a radius of 5 meters and a height of 10 meters?
Solution:
Using the formula V = 1/3πr²h, we can substitute the given values: V = 1/3π(5 m)²(10 m) = 1/3π(25 m²)(10 m) = 1/3π(250 m³) = 261.80 m³ (rounded to two decimal places).
- For each practice problem, remember to check your units and round your final answer to the appropriate number of decimal places.
- If the height or radius is not given in the same units, make sure to convert one of them to match the other before plugging them into the formula.
- Pay attention to any special instructions or restrictions given in the problem.
With these practice problems, you can improve your skills in calculating the volume of cones and gain confidence in using the formula V = 1/3πr²h. Remember to practice using different values for the radius and height to further strengthen your understanding of this concept.
Importance of Volume of Cone Worksheet

The concept of volume is an essential topic in mathematics, and it plays a crucial role in various real-world applications. When it comes to three-dimensional objects, understanding their volume is necessary for calculations, comparisons, and problem-solving. One such three-dimensional object is a cone, which has a unique shape and properties.
A volume of cone worksheet provides students with an opportunity to practice and reinforce their understanding of how to calculate the volume of a cone. It typically includes a variety of problems involving different cone dimensions, such as radius, height, and slant height. By solving these problems, students can develop their skills in finding the volume of a cone and apply the formula correctly.
The worksheet format allows for a structured and organized approach to learning. Students can follow the instructions provided in the worksheet, solve the given problems, and check their answers using the provided answer key. This process helps students become familiar with the volume formula for a cone and gain confidence in their ability to apply it correctly.
Understanding the volume of a cone is not only important for mathematics but also for various fields such as architecture, engineering, and physics. Architects use volume calculations to determine the capacity of structures, engineers use it to design efficient structures, and physicists use it to study the behavior of fluids and other materials.
In conclusion, a volume of cone worksheet is a valuable resource for students to practice and master the concept of finding the volume of a cone. It helps them develop their mathematical skills, apply the volume formula correctly, and understand the real-world applications of volume calculations. By working through these worksheets, students can strengthen their knowledge and become proficient in solving cone-related volume problems.
Common Mistakes to Avoid when Calculating the Volume of a Cone
Calculating the volume of a cone is a fundamental skill in geometry, but it can be easy to make mistakes if you’re not careful. Here are some common mistakes to avoid when calculating the volume of a cone:
- Forgetting to divide by 3: One of the most common mistakes is forgetting to divide the result of the volume formula by 3. The volume formula for a cone is V = 1/3 * π * r^2 * h, where r is the radius of the base and h is the height. It’s important to remember to divide the result by 3, as this is the correct way to calculate the volume of a cone.
- Using the wrong measurements: Another common mistake is using the wrong measurements for the radius and height of the cone. Make sure to double-check that you are using the correct values for these variables in the volume formula. Using the wrong measurements will result in an incorrect volume calculation.
- Not converting units: If the measurements for the radius and height are given in different units, it’s important to convert them to the same unit before calculating the volume. For example, if the radius is given in inches and the height is given in centimeters, you will need to convert one of the measurements to match the other. Forgetting to convert units can lead to inaccurate volume calculations.
- Mistakes in arithmetic: Simple arithmetic errors can easily occur when calculating the volume of a cone. It’s important to double-check your calculations to ensure accuracy. Pay attention to the order of operations and be careful with decimal points and fractions.
- Using the wrong formula: Lastly, using the wrong formula for calculating the volume of a cone can result in an incorrect answer. Make sure to use the correct formula, V = 1/3 * π * r^2 * h, and not confuse it with the formulas for other geometric shapes.
Avoiding these common mistakes will help ensure that you accurately calculate the volume of a cone. Remember to double-check your calculations and use the correct formula, and you’ll be on your way to mastering this important geometric concept.
Tips to Improve your Understanding of Finding the Volume of a Cone
If you are struggling with finding the volume of a cone, there are several tips and tricks that can help you improve your understanding of this concept. Whether you are a student studying for an exam or someone who wants to refresh their math skills, these tips will guide you towards mastering the calculation of cone volumes.
1. Understand the Formula: First, it’s essential to understand the formula for calculating the volume of a cone. The formula is V = 1/3 * π * r^2 * h, where V represents the volume, π is a mathematical constant (approximately equal to 3.14159), r is the radius of the base of the cone, and h is the height of the cone. Knowing and understanding this formula is the first step towards finding the volume accurately.
2. Practice with Example Problems: To gain proficiency in finding the volume of a cone, it’s crucial to practice with example problems. Work through a variety of different problems with different values for the radius and height of the cone. This will help you understand how the volume changes with these variables and reinforce your understanding of the formula.
3. Break Down the Problem: When faced with a complex cone volume problem, break it down into smaller, more manageable parts. For example, if the problem involves a cone with a slanted height or an oblique cone, break it down into smaller right triangles and calculate the volumes of those triangles individually. Then, add up the volumes to find the total volume of the cone.
4. Visualize the Cone: To better understand the concept of cone volume, try visualizing the cone in your mind’s eye. Imagine the cone being filled with water or sand, and think about how much space it would take up. This visualization can help you grasp the concept of volume better and make it easier to solve related problems.
5. Seek Help if Needed: If you are still struggling to understand the volume of a cone concept, don’t hesitate to seek help. You can ask your teacher, instructor, or a math tutor for clarification and additional guidance. Sometimes, hearing the explanation from a different perspective can make all the difference in your understanding.
By following these tips, you can improve your understanding of finding the volume of a cone and become more confident in solving cone volume problems. Remember, practice and perseverance are key to mastering any mathematical concept.