
In geometry, the volume of a pyramid or a cone is a fundamental concept that is often taught in mathematics classes. Understanding how to calculate the volume of these three-dimensional shapes is important for solving various real-life problems and for further studies in geometry and calculus.
A pyramid is a polyhedron with a polygonal base and triangular faces that converge to a common vertex. On the other hand, a cone is a three-dimensional figure with a circular base and a curved surface that tapers to a point called the apex. The volume of both pyramids and cones can be calculated using specific formulas that depend on the shape and dimensions of the base and height.
The formula to calculate the volume of a pyramid is 1/3 times the area of the base multiplied by the height. This means that the volume of a pyramid will be smaller if the base is smaller or if the height is shorter. Similarly, the formula to calculate the volume of a cone is 1/3 times the area of the base multiplied by the height. However, in the case of a cone, the base is circular, so the area of the base is calculated using the formula for the area of a circle, which is π times the radius squared.
By understanding the formulas and following step-by-step calculations, students can find the volume of pyramids and cones. This knowledge can be applied to solve various problems in architecture, engineering, and physics, where the volume of these shapes is crucial. By practicing these calculations, students can develop their spatial reasoning skills and become more proficient in geometry.
Volume of Pyramids and Cones Answer Key
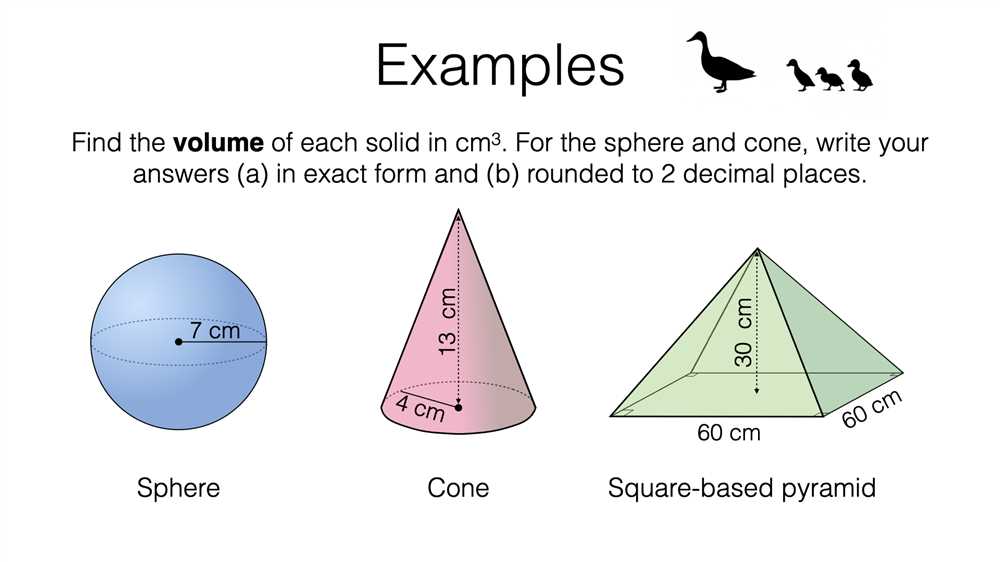
Calculating the volume of pyramids and cones requires a solid understanding of their respective formulas and measurement units. By using the provided answer key, students can check their calculations and ensure they are on the right track.
Pyramids: To find the volume of a pyramid, students need to multiply the area of the base by the height and divide the result by 3. The formula for the volume of a pyramid is V = (1/3) * B * h, where V represents the volume, B is the area of the base, and h is the height of the pyramid. By plugging in the given values and following the necessary steps, students can arrive at the correct volume measurement.
Cones: Determining the volume of a cone follows a similar process. Students must multiply the area of the base by the height and divide the result by 3, just like with pyramids. However, the formula for the volume of a cone includes an additional constant, π (pi). The formula for calculating the volume of a cone is V = (1/3) * π * r² * h, where V represents the volume, r is the radius of the base, and h is the height of the cone. It is important for students to use the correct value for π when performing their calculations.
Answer Key Importance: The answer key plays a crucial role in the learning process. It allows students to self-assess, identify any errors they may have made, and learn from their mistakes. It also provides a reference point for understanding the correct approach and method to solve volume problems involving pyramids and cones. Students can compare their answers with the answer key to determine whether they have correctly applied the formulas and concepts learned in class.
In conclusion, the volume of pyramids and cones answer key is an invaluable resource for students studying these geometric shapes. It helps them verify their calculations, improve their problem-solving skills, and gain a deeper understanding of the formulas and concepts involved. By utilizing the answer key effectively, students can confidently solve volume problems and achieve success in their mathematics studies.
Understanding Volume

Volume is a fundamental concept in mathematics and physics that measures the amount of space occupied by an object. It is often referred to as the capacity or size of an object. Understanding volume is crucial in various fields, including architecture, engineering, and manufacturing.
Definition: Volume is the measure of how much space occupies a three-dimensional object. It is typically expressed in cubic units, such as cubic centimeters (cm³) or cubic meters (m³).
Calculating Volume: The formula for calculating the volume of a solid object depends on its shape. For example, the volume of a rectangular prism can be calculated by multiplying its length, width, and height. The volume of a cylinder can be calculated by multiplying the area of its base by its height.
Volume of Pyramids and Cones: In the context of pyramids and cones, the volume formula is slightly different. The volume of a pyramid can be calculated by multiplying the area of its base by the height and dividing the result by 3. The volume of a cone can be calculated by multiplying the area of its base by its height and dividing the result by 3 as well.
The concept of volume can be visualized using various methods, such as using cubes to fill the object and counting the number of cubes or using water displacement to measure the volume. Understanding volume is essential for solving real-life problems, such as determining the capacity of containers or calculating the materials needed for construction projects. It is also important in understanding the principles of buoyancy and fluid mechanics.
- Volume is a measure of space occupied by an object.
- Calculating volume depends on the shape of the object.
- The volume of pyramids and cones can be calculated using specific formulas.
- Understanding volume is crucial in architecture, engineering, and manufacturing.
- Visualizing volume can be done using cubes or water displacement.
Volume of a Pyramid
A pyramid is a three-dimensional geometric shape with a polygonal base and triangular faces that converge at a single point called the apex or vertex. The volume of a pyramid is the measure of the space enclosed within its boundaries. It is a crucial concept in geometry and has various real-world applications.
To find the volume of a pyramid, you need to know the dimensions of its base and its height. The formula for finding the volume of a pyramid is:
Volume = (1/3) * base area * height
The base area refers to the area of the polygonal base of the pyramid, and the height is the perpendicular distance from the base to the apex. The formula reflects the fact that a pyramid can be thought of as one-third of a prism with the same base and height.
Calculating the volume of a pyramid is relatively straightforward once you know the base area and height. However, it is essential to ensure that the measurements are in the same units. For example, if the base area is given in square centimeters, the height should also be in centimeters to get the volume in cubic centimeters.
Understanding the concept of the volume of a pyramid is crucial in various fields such as architecture, engineering, and construction. It helps determine the amount of material needed for pyramid-shaped structures and aids in designing structures that optimize space utilization.
Volume of a Cone
A cone is a three-dimensional shape with a circular base and a pointed top. To find the volume of a cone, you can use the formula V = 1/3 * π * r^2 * h, where V represents the volume, π is a mathematical constant approximately equal to 3.14159, r is the radius of the base, and h is the height of the cone.
Let’s break down the formula step by step. The first step is to find the area of the base, which is given by the formula A = π * r^2, where A represents the area and r is the radius of the base. The radius is the distance from the center of the base to any point on its edge. Once you have the area of the base, multiply it by the height of the cone and divide by 3 to obtain the volume.
For example, let’s say we have a cone with a radius of 4 units and a height of 6 units. First, find the area of the base by plugging the radius into the formula A = π * r^2. The area is then 16π square units. Next, multiply the area by the height and divide by 3: (16π * 6)/3 = 32π cubic units. So the volume of the cone is 32π cubic units.
Remember that the volume of a cone is always one-third of the volume of a cylinder with the same base and height. This relationship can be visualized by imagining stacking three cones on top of each other to form a cylinder. So if you know the volume of a cylinder, you can easily find the volume of a cone by dividing it by 3.
In summary, the volume of a cone can be found using the formula V = 1/3 * π * r^2 * h, where V is the volume, π is the mathematical constant, r is the radius of the base, and h is the height of the cone. Remember that the volume of a cone is always one-third of the volume of a cylinder with the same base and height.
Examples and Practice Problems
In order to fully understand and apply the concepts of finding the volume of pyramids and cones, it is important to practice solving various examples and practice problems. By doing so, you can reinforce your understanding of the formulas and techniques involved.
Here are some examples and practice problems to help you practice calculating the volume of pyramids and cones:
- Example 1: Find the volume of a pyramid with a base area of 25 square units and a height of 10 units.
- Example 2: A cone has a radius of 5 units and a height of 12 units. Calculate its volume.
- Practice Problem 1: A pyramid has a triangular base with base edges of length 8 units, 10 units, and 12 units. The height of the pyramid is 6 units. Find its volume.
- Practice Problem 2: A cone has a diameter of 6 units and a height of 9 units. Determine its volume.
Remember to use the appropriate formulas for calculating the volume of pyramids and cones. For pyramids, the formula is V = (1/3) * base area * height. For cones, the formula is V = (1/3) * π * radius^2 * height. Apply these formulas to each example and practice problem to find their respective volumes.
By practicing these examples and problems, you can enhance your ability to calculate the volumes of pyramids and cones accurately and efficiently. It is crucial to understand the formulas and concepts involved in order to excel in geometry and related subjects.
Common Mistakes to Avoid
When calculating the volume of pyramids and cones, there are several common mistakes that students often make. By being aware of these mistakes, you can avoid them and ensure accurate calculations.
Mistake 1: Incorrectly identifying the height. One common mistake is not properly identifying the height of the pyramid or cone. The height is always the perpendicular distance from the base to the vertex or apex of the shape. Incorrectly identifying the height can lead to incorrect volume calculations.
Mistake 2: Using the wrong formula. Another common mistake is using the wrong formula to calculate the volume. For a pyramid, the volume formula is 1/3 times the area of the base times the height. For a cone, the volume formula is 1/3 times the area of the base times the height. Using the wrong formula will result in incorrect volume calculations.
Mistake 3: Forgetting to divide by 3. Many students forget to divide the calculated volume by 3 when using the correct formula. This is a critical step because it accounts for the fact that a pyramid or cone is a third of a prism or cylinder with the same base and height.
Mistake 4: Incorrectly calculating the area of the base. Another common mistake is incorrectly calculating the area of the base. It is important to accurately measure the dimensions of the base shape and use the correct formula (e.g., area of a triangle for a pyramid, area of a circle for a cone). Incorrectly calculating the base area will lead to incorrect volume calculations.
To avoid these common mistakes, always make sure to accurately identify the height, use the correct formula, divide by 3 when necessary, and correctly calculate the area of the base. By doing so, you can confidently calculate the volume of pyramids and cones without any errors.
Real-World Applications
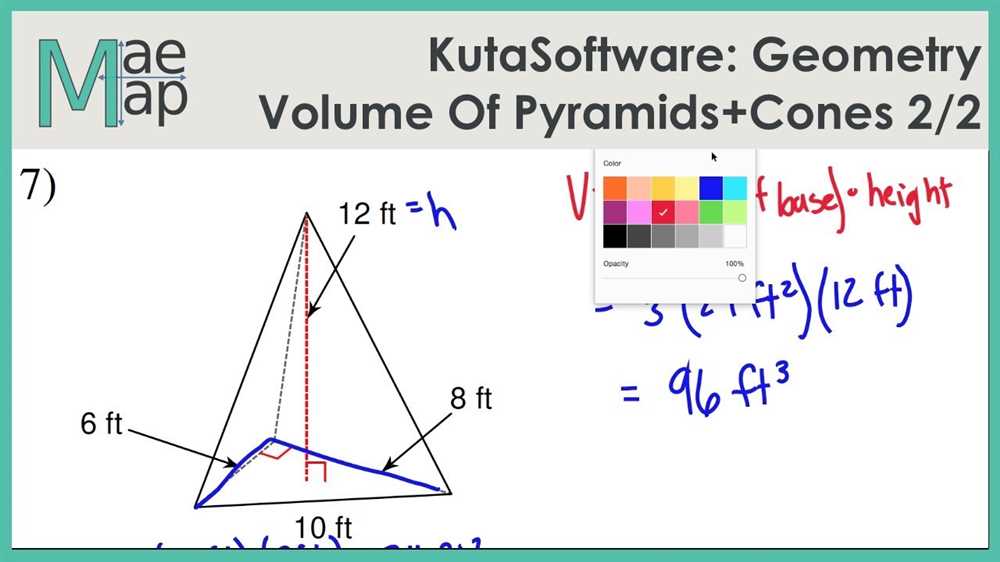
In real-world scenarios, the concept of volume is often used to solve practical problems related to pyramids and cones.
For example, in architecture and construction, the volume of a pyramid can be calculated to determine the amount of material needed to build it. By finding the volume, architects and engineers can estimate the quantity of concrete, stones, or other building materials required for the pyramid’s construction.
The volume of cones is also important in various industries, such as the food and beverage industry. Packaging companies need to determine the volume of cones, such as ice cream cones or wafer cones, to ensure that the right amount of product can be held. Additionally, the volume of cones is used by manufacturers of traffic cones to determine the amount of material needed to produce a certain number of cones.
In the field of manufacturing, the concept of volume is crucial for quality control. For example, the volume of molded parts, such as plastic bottles or containers, needs to be measured accurately to ensure that they meet the required specifications. By calculating and comparing the volumes of these objects, manufacturers can identify any variations or defects, allowing them to maintain consistent product quality.
Furthermore, the volume of pyramids and cones is used in everyday life situations as well. For instance, when filling up a cone-shaped container, determining its volume can help ensure that the right amount of liquid or granular material is added without overflow or wastage. Similarly, in cooking and baking, knowing the volume of a cone-shaped measuring cup can help achieve precise measurements for ingredients like flour or sugar.