
Calculating the volume of a sphere is a fundamental concept in mathematics and geometry. It plays a crucial role in various fields, including physics, engineering, and architecture. The volume of a sphere can be determined by using a specific formula that takes into account its radius or diameter.
To find the volume of a sphere, one must first understand the concept of a sphere. A sphere is a three-dimensional geometric shape that has a curvature similar to that of a perfectly round ball. It is defined as the set of all points in space that are equidistant from a center point. The radius of a sphere is the distance from the center point to any other point on the surface.
The formula used to calculate the volume of a sphere is V = 4/3πr^3, where V represents volume and r represents the radius of the sphere. This formula shows that the volume of a sphere is directly proportional to the cube of its radius. In other words, if the radius of a sphere is increased, its volume will increase by a factor of the cube of that increase.
Understanding the volume of a sphere is important for a variety of reasons. It allows us to determine the amount of space occupied by a sphere, which is useful for calculating quantities like the amount of liquid that can fill a spherical container. Additionally, it provides insights into the geometric properties of spheres, such as their capacity for enclosing other shapes.
In conclusion, the volume sphere answer key provides a method for calculating the volume of a sphere based on its radius or diameter. By understanding the concept of a sphere and using the appropriate formula, one can accurately determine the amount of space occupied by this three-dimensional shape. The volume of a sphere has practical applications in various fields and helps to deepen our understanding of its geometric properties.
The volume of a sphere is a measure of the amount of space inside the sphere. It is commonly calculated using the formula V = (4/3)πr^3, where V represents the volume and r represents the radius of the sphere. This formula can be used to find the volume of any sphere, regardless of its size or dimensions.
To use the formula, simply insert the radius value into the equation and calculate the result. For example, if the radius of a sphere is 5 units, the volume can be found by substituting r = 5 into the formula: V = (4/3)π(5^3) = (4/3)π(125) = 523.6 cubic units. The answer should be rounded to the nearest tenth.
Example Calculation:
- Radius of sphere (r) = 5 units
- Volume of sphere (V) = (4/3)π(5^3)
- Volume of sphere (V) = (4/3)π(125)
- Volume of sphere (V) = 523.6 cubic units (rounded to the nearest tenth)
It is important to note that the value of π, which is a mathematical constant representing the ratio of a circle’s circumference to its diameter, is approximately 3.14159. When calculating the volume of a sphere, it is recommended to use a more accurate value of π, such as 3.14159265358979323846.
In conclusion, the volume of a sphere can be calculated using the formula V = (4/3)πr^3, where V represents the volume and r represents the radius of the sphere. By plugging in the radius value, the volume can be determined and represented in cubic units. The value of π should be approximated to a sufficient number of decimal places for accuracy.
Understanding the Volume of a Sphere
The volume of a sphere is a fundamental concept in geometry and can be derived using various mathematical formulas. The volume refers to the amount of space enclosed by a sphere, and it is important to understand how to calculate it for practical applications in fields such as engineering and physics.
The formula to calculate the volume of a sphere is V = (4/3)πr³, where V represents the volume and r is the radius of the sphere. The symbol π, or pi, is a mathematical constant approximately equal to 3.14159. This formula can be used to determine the volume of any sphere, regardless of its size.
To visualize the concept, imagine a three-dimensional object with a perfectly symmetrical round shape, such as a ball. The volume of this object can be thought of as the amount of water it can hold, or the amount of space it occupies. The volume of a sphere is determined solely by its radius, as larger spheres will have greater volumes than smaller ones with the same radius.
Calculating the volume of a sphere is a straightforward process once the formula is understood. Simply input the radius of the sphere into the formula and perform the necessary calculations. It is crucial to use the correct units when entering the radius to ensure accurate results. The resulting volume will be in cubic units, such as cubic centimeters or cubic meters, depending on the units used for the radius.
In conclusion, understanding the volume of a sphere is essential for various fields of study and practical applications. By utilizing the formula V = (4/3)πr³, one can accurately calculate the volume of any sphere based on its radius. This knowledge is crucial when dealing with spheres in real-world scenarios, allowing for accurate calculations and measurements.
The Formula for Volume of a Sphere
The volume of a sphere can be calculated using a simple formula. A sphere is a three-dimensional shape with all points on its surface equidistant from its center. The formula for volume of a sphere is:
V = (4/3)πr3
This formula shows that the volume of a sphere is directly proportional to the cube of its radius. This means that as the radius of a sphere increases, its volume increases exponentially. Similarly, as the radius decreases, the volume decreases exponentially.
The value of π (pi) is an irrational number approximately equal to 3.14159. It is a mathematical constant that relates the circumference of a circle to its diameter. In the formula for volume of a sphere, π is used to calculate the precise volume.
To calculate the volume of a sphere, you need to know the radius of the sphere. The radius is the distance from the center of the sphere to any point on its surface. Once you have the radius, you can plug it into the formula and calculate the volume using basic arithmetic operations.
For example, let’s say you have a sphere with a radius of 5 units. By plugging this value into the formula, the calculation would be:
V = (4/3)π(5)3
By simplifying the equation, we get:
V = (4/3)π(125)
Finally, by multiplying and dividing:
V ≈ 523.6 cubic units
Therefore, the volume of the sphere with a radius of 5 units is approximately 523.6 cubic units.
Step-by-Step Guide to Calculating the Volume of a Sphere
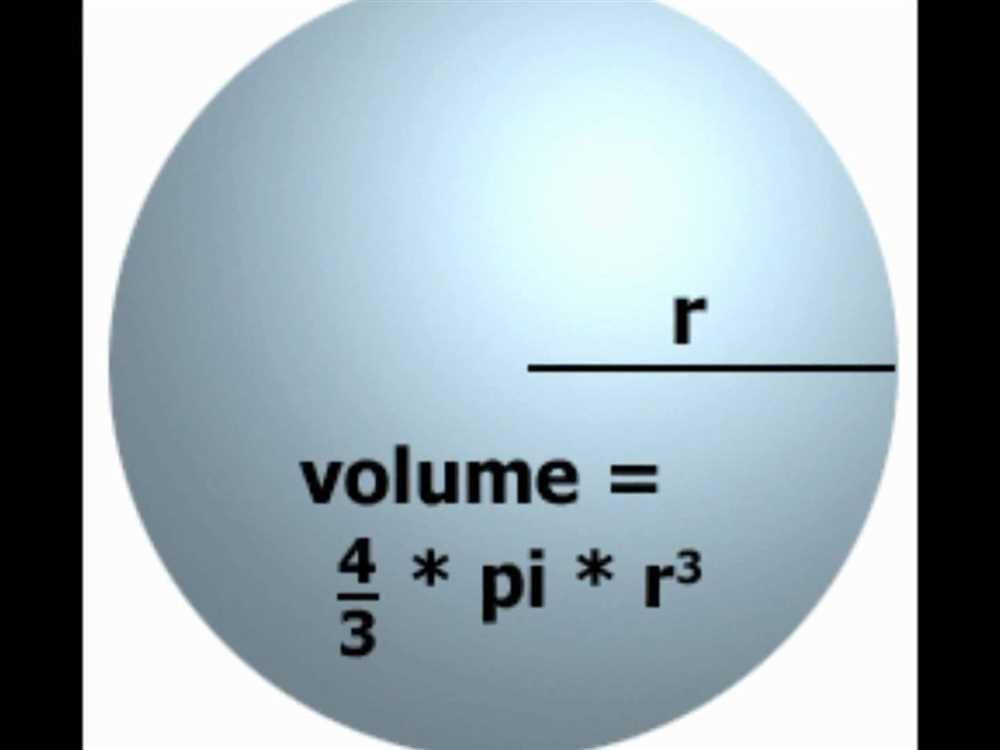
Calculating the volume of a sphere may seem intimidating at first, but it can be broken down into a straightforward step-by-step process. By following these steps, you’ll be able to find the volume of a sphere with confidence.
Step 1: Understand the Formula
The formula to calculate the volume of a sphere is V = (4/3)πr³. In this formula, V represents the volume, π is a mathematical constant approximately equal to 3.14159, and r is the radius of the sphere. Make sure you have a clear understanding of this formula before proceeding to the next steps.
Step 2: Measure the Radius
To begin, you’ll need to measure the radius of the sphere. The radius is the distance from the center of the sphere to its outer surface. Use a ruler or any other appropriate measuring tool to obtain an accurate measurement of the radius.
Step 3: Calculate the Radius cubed (r³)
Once you have the radius measurement, cube it by multiplying the radius by itself twice. For example, if the radius is 5 units, you would calculate 5³, which equals 125.
Step 4: Multiply by (4/3)π
Next, multiply the result from step 3 by (4/3)π. Use the value of π as approximately 3.14159. Continuing with the previous example, multiply 125 by (4/3)π to get the volume of the sphere.
Step 5: Round and Label
Lastly, round the final volume calculation to the appropriate decimal place, depending on the desired level of precision. Don’t forget to include the relevant unit of measurement for the volume, such as cubic units, in the final answer.
By diligently following these steps, you’ll be able to confidently calculate the volume of a sphere using its radius. Remember to double-check your measurements and calculations to ensure accuracy in your results.
Examples of Volume Calculations for Spheres
Calculating the volume of a sphere is an important mathematical concept that is used in various fields such as physics, engineering, and architecture. The volume of a sphere can be calculated using the formula V = (4/3)πr^3, where V is the volume and r is the radius of the sphere. Here are some examples of volume calculations for spheres:
Example 1:
Let’s say we have a sphere with a radius of 5 units. Using the formula V = (4/3)πr^3, we can calculate its volume as follows:
V = (4/3)π(5^3) = (4/3)π(125) = 166.67π cubic units.
The volume of the sphere is approximately equal to 523.6 cubic units.
Example 2:
Suppose we have a larger sphere with a radius of 10 meters. To find its volume, we can apply the same formula:
V = (4/3)π(10^3) = (4/3)π(1000) = 4000π cubic meters.
The volume of this sphere is approximately equal to 12,566.37 cubic meters.
Example 3:
Let’s consider a scenario where the radius is given in terms of diameter. If the diameter of a sphere is 8 centimeters, we can calculate its volume as follows:
First, we need to find the radius by dividing the diameter by 2: r = 8/2 = 4 centimeters.
Using the formula V = (4/3)πr^3, we can now calculate the volume:
V = (4/3)π(4^3) = (4/3)π(64) = 268.08π cubic centimeters.
The volume of this sphere is approximately equal to 841.93 cubic centimeters.
These examples demonstrate the application of the volume formula for spheres and highlight how the volume can be calculated for spheres of different sizes. It is important to understand the concept of volume and be able to apply the appropriate formula to solve problems involving spheres.
Common Mistakes in Calculating the Volume of a Sphere
Calculating the volume of a sphere is an important skill in geometry and often comes up in math classes and real-world applications. However, many students make common mistakes when attempting to find the volume of a sphere, leading to incorrect answers. Understanding these mistakes can help improve accuracy and ensure the correct calculation of the sphere’s volume.
1. Incorrectly using the wrong formula: One of the most common mistakes is using the wrong formula to find the volume of a sphere. The correct formula is V = (4/3)πr^3, where V represents volume and r represents the radius of the sphere. Students may mistakenly use the formula for the surface area of a sphere or confuse it with other formulas, resulting in an incorrect volume calculation.
2. Misinterpreting the radius: Another mistake often made is misinterpreting the radius of the sphere. The radius is the distance from the center of the sphere to any point on its surface. However, some students mistakenly use the diameter instead, which is twice the length of the radius. This error can lead to an incorrect volume calculation since the radius should be used in the formula.
3. Not using the correct value for Pi: Pi (π) is an irrational number that represents the ratio of a circle’s circumference to its diameter. When calculating the volume of a sphere, it is crucial to use the correct value for Pi, typically rounded to 3.14 or expressed as π. Students may use an approximate value or forget to include Pi altogether, resulting in an inaccurate volume calculation.
4. Failing to simplify the equation: The formula for the volume of a sphere includes the fraction (4/3). Some students may forget to simplify this fraction, leading to incorrect answers. It is essential to simplify the fraction to its decimal equivalent (1.33) or use the fraction form to ensure an accurate volume calculation.
5. Not paying attention to units: Units play a crucial role in determining the volume of a sphere. Students should ensure that the radius they use matches the units of the sphere’s volume required in the problem. For example, if the problem requires the volume in cubic centimeters, the radius should be in centimeters as well. Failure to pay attention to units can result in incorrect volume calculations.
By understanding these common mistakes and practicing the correct methods, students can improve their accuracy in calculating the volume of a sphere. It is essential to double-check each step of the calculation and be mindful of the formula, radius, Pi value, simplification, and units to ensure an accurate volume result.
Applications of Volume of a Sphere in Real Life
The volume of a sphere is a concept that has many practical applications in various fields. From engineering to architecture, medicine to geology, understanding the volume of a sphere is essential for solving real-life problems. Here are some practical applications where the concept of volume of a sphere is used:
1. Manufacturing and Designing of Round Containers
The volume of a sphere is commonly used in the manufacturing and designing of round containers such as cans, bottles, and storage tanks. By calculating the volume, manufacturers can determine the amount of material needed to produce a specific container. Additionally, architects and designers use the volume of a sphere to create aesthetically pleasing structures like domes and arches.
2. Calculating the Amount of Liquid or Gas in Storage Tanks

Storage tanks used in industries often have a spherical shape. Understanding the volume of a sphere helps in calculating the amount of liquid or gas stored in these tanks. This information is crucial for inventory management, transportation, and monitoring the usage of resources.
3. Determining the Dosage of Medications
Medical professionals utilize the volume of a sphere when determining the dosage of medications. For example, the volume of a pill or a capsule can be calculated using the sphere formula, allowing doctors to prescribe accurate dosages based on a patient’s needs. This knowledge helps in preventing under or overdose of medications.
4. Simulating Planetary Bodies in Astronomy
Astronomers and physicists use the concept of volume of a sphere to simulate planetary bodies and celestial objects. By understanding the volume, they can measure the mass, density, and gravitational force exerted by these bodies. This information is crucial for analyzing the behavior of planets, stars, and other celestial entities.
In conclusion, the volume of a sphere has numerous practical applications in our everyday lives. Whether it’s designing containers, calculating medication dosages, or understanding the universe, the concept of volume of a sphere plays a crucial role in various fields. Its applications extend beyond theoretical mathematics, making it a fundamental concept with real-world significance.