When studying functions, it is important to have a thorough understanding of their properties and behavior. The process of analyzing functions involves examining various aspects, such as domain, range, intercepts, symmetry, and transformations. This article will provide answers to the exercises related to analyzing functions in the 1.1-1.4 section.
One key concept in analyzing functions is the domain, which refers to the set of all possible input values for a function. By determining the domain, we can identify any restrictions or limitations on the input values. For example, if a function contains a square root, the domain would exclude any negative numbers that would result in an imaginary output. Evaluating the domain helps us understand where the function is defined.
Another important aspect of analyzing functions is the range, which refers to the set of all possible output values for a function. The range helps us determine the span of the function’s outputs and whether there are any limitations or restrictions on the output values. By analyzing the range, we can gain insights into the function’s behavior and understand how the output varies with different input values.
Intercepts are also crucial for understanding functions. An x-intercept is a point at which a function crosses the x-axis, meaning the output value is zero. Similarly, a y-intercept is a point at which a function crosses the y-axis, meaning the input value is zero. Analyzing the intercepts can help us determine the behavior of a function and identify any key points.
Overview of 1.1-1.4 Analyzing Functions Answers
In the sections 1.1-1.4 of analyzing functions, we explored various concepts related to functions and their properties. This overview provides a summary of the key answers and insights gained from these sections.
Section 1.1:
- A function is a mathematical relation defined by a set of input values called the domain and a set of output values called the range.
- A function can be represented in various forms, including algebraic, graphical, and tabular representations.
- The vertical line test is used to determine if a relation is a function. If any vertical line intersects the graph of the relation at more than one point, then the relation is not a function.
Section 1.2:
- The domain of a function is the set of input values for which the function is defined.
- The range of a function is the set of output values that the function can produce.
- The domain and range of a function can be determined by analyzing the algebraic expression, graph, or table of values associated with the function.
Section 1.3:
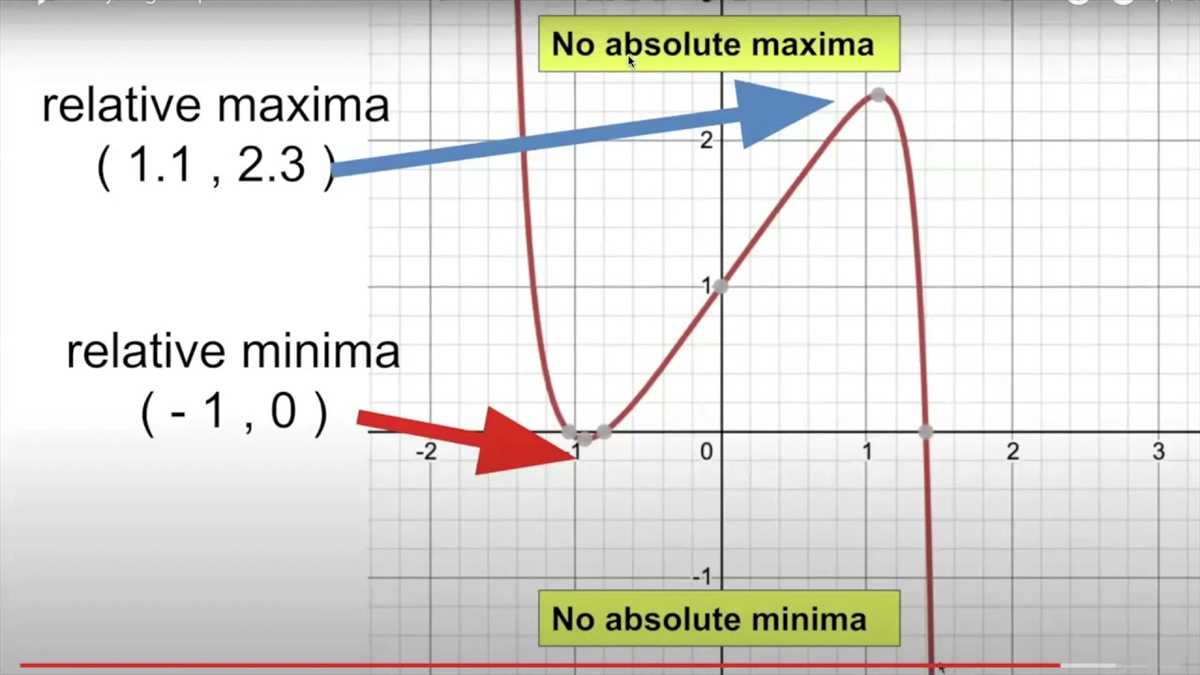
- The key features of a function include its domain, range, intercepts, symmetry, intervals of increase or decrease, local extrema, and end behavior.
- The intercepts of a function are the points where the graph of the function intersects the x-axis (x-intercepts) and the y-axis (y-intercepts).
- Symmetry in a function can be determined by analyzing its algebraic expression or graph. Functions can exhibit symmetry about the x-axis, y-axis, or the origin.
Section 1.4:
- Interval notation is used to represent intervals on a number line. It is written in the form [a, b], where a and b are the endpoints of the interval. The interval can be inclusive or exclusive, depending on whether or not the endpoints are included.
- By analyzing the sign of the derivative of a function, we can determine the intervals where the function is increasing or decreasing.
- A local extrema of a function is a point where the function reaches a maximum or minimum value within a specific interval.
Overall, analyzing functions involves understanding their domain, range, graphical representation, symmetry, intercepts, and the behavior of the function within specific intervals. These concepts provide a foundational understanding of functions and their properties.
Exploring the Concept of Analyzing Functions
When it comes to mathematics, analyzing functions plays a crucial role in understanding the relationships between variables. By examining the behavior of a function, we can gain insights into its properties, such as the domain, range, and graph. Through the study of analyzing functions, we can make predictions, solve equations, and tackle real-world problems.
One of the key aspects of analyzing functions is determining the domain, which refers to the set of input values for which the function is defined. This step is essential because it helps us understand the restrictions on the independent variable. By identifying any exclusions or limitations, we can ensure that our analysis is accurate and relevant.
The range, on the other hand, corresponds to the set of output values that the function can produce. Similar to the domain, determining the range allows us to understand the behavior of the dependent variable. It provides us with valuable information about the function’s behavior and potential values it can take on.
Furthermore, analyzing functions involves examining the graph of the function. By plotting points on a coordinate plane, we can visualize how the function behaves and identify any patterns or trends. Understanding the shape, intercepts, and symmetry of the graph provides us with significant insights into the function’s behavior, and can help answer questions about its maximum and minimum values, increasing or decreasing intervals, and asymptotic behavior.
In conclusion, analyzing functions is a fundamental concept in mathematics that allows us to understand the relationships between variables. By examining the domain, range, and graph of a function, we can gain valuable insights into its behavior and make predictions about its properties. This analytical approach is essential for solving equations, making calculations, and addressing real-world problems.
Key Concepts in Analyzing Functions
When analyzing functions, there are several key concepts that are important to understand. These concepts help us understand and interpret the behavior of functions and their graphs.
Domain and Range:
The domain of a function is the set of all possible input values, or x-values, for which the function is defined. It represents the values that can be plugged into the function. The range of a function is the set of all possible output values, or y-values, that the function can produce. It represents the values that the function can output as a result of the inputs. The domain and range can help us determine the boundaries and limitations of a function.
Function Notation:
Function notation is a way to represent functions using symbols and expressions. It allows us to write and manipulate functions algebraically. The standard form of function notation is f(x), where f is the name of the function and x is the input variable. This notation helps us differentiate between the function itself and the specific inputs. By using function notation, we can evaluate functions, perform operations on them, and analyze their properties.
Graphical Representation:
Graphing functions is a visual way to represent their behavior. The graph of a function shows the relationship between the input and output values. It can provide information about the shape, direction, and key points of the function. By analyzing the graph, we can determine whether the function is increasing or decreasing, find its zeros or intercepts, and identify any asymptotes or discontinuities. Graphical representation helps us visualize and interpret the behavior of functions.
Operations on Functions:
Functions can be combined and manipulated using various operations. Common operations include addition, subtraction, multiplication, division, composition, and transformation. These operations allow us to create new functions from existing ones, alter the shape or position of functions, and perform calculations on functions. By understanding operations on functions, we can analyze their properties, make connections between different functions, and solve problems involving multiple functions.
Tips for Analyzing Functions
Analyzing functions is an important skill in mathematics and can help us understand their behavior and properties. Here are some tips to keep in mind when analyzing functions:
1. Determine the domain and range:
Before diving into the analysis of a function, it is crucial to determine the domain and range of the function. The domain represents all possible input values for the function, while the range represents all possible output values. This information provides the boundaries for our analysis.
2. Identify key points:
Identify the key points of the function, such as intercepts, extrema (maximum and minimum points), points of inflection, and asymptotes. These points can provide valuable insights into the behavior of the function and help in sketching its graph.
3. Determine symmetry:
Check for symmetry in the function. An even function is symmetric with respect to the y-axis, meaning that replacing x with -x does not change the value of the function. An odd function is symmetric with respect to the origin, meaning that replacing x with -x changes the sign of the function. Symmetry can simplify the analysis by reducing the number of calculations required.
4. Analyze increasing and decreasing intervals:
Examine the intervals where the function is increasing or decreasing. This can be done by finding the intervals where the derivative of the function is positive or negative, respectively. These intervals can help us understand the behavior of the function and locate its extrema.
5. Check for concavity:
Check for the concavity of the function. A function is concave up if its second derivative is positive and concave down if its second derivative is negative. The points of inflection occur where the concavity changes. Understanding the concavity can help us determine the shape of the graph.
By following these tips, we can effectively analyze functions and gain a deeper understanding of their behavior and properties.
Common Challenges in Analyzing Functions
When analyzing functions, there are several challenges that mathematicians and statisticians commonly encounter. These challenges can range from understanding the behavior of the function to identifying the key features that influence its values. In this article, we will explore some of the common challenges faced in analyzing functions and provide insights on how to overcome them.
1. Understanding the Behavior of the Function
One of the main challenges in analyzing functions is gaining an understanding of their behavior. This involves determining whether the function is increasing, decreasing, or neither over a given interval, as well as identifying any critical points such as maximum or minimum values. To overcome this challenge, it is crucial to study the derivative of the function, which provides information about its rate of change and the presence of extrema.
2. Identifying Key Features
Another common challenge is identifying the key features of a function that have the most significant impact on its values. These features can include the domain and range of the function, symmetry, intercepts, asymptotes, and periods. To address this challenge, it is essential to carefully examine the algebraic representation of the function and apply mathematical techniques such as factoring or completing the square.
Overall, analyzing functions requires a combination of mathematical knowledge, critical thinking skills, and attention to detail. By understanding the behavior of the function and identifying its key features, mathematicians and statisticians can gain valuable insights into how the function behaves and make informed decisions based on its properties.
In conclusion, analyzing functions can be challenging due to the need to understand their behavior and identify key features that influence their values. However, by studying the derivative of the function and carefully examining its algebraic representation, mathematicians and statisticians can overcome these challenges and gain valuable insights into the function’s properties.
Examples of Analyzing Functions
A function represents a relationship between two sets, where each input value from the first set corresponds to exactly one output value from the second set. Analyzing functions involves understanding their behavior, such as the domain and range, symmetry, and transformations. Here are some examples of how to analyze functions:
Example 1: Quadratic Function
A quadratic function is in the form of f(x) = ax^2 + bx + c, where a, b, and c are constants. To analyze a quadratic function, we can determine its vertex, axis of symmetry, and whether it opens upward or downward. The vertex is the highest or lowest point of the function, and the axis of symmetry is the vertical line that passes through the vertex. The sign of the coefficient a determines whether the parabola opens upward (if a > 0) or downward (if a < 0). Additionally, we can find the x-intercepts by setting f(x) equal to zero and solving for x.
Example 2: Exponential Function
An exponential function is in the form of f(x) = a^x, where a is a positive constant. When analyzing an exponential function, we can determine its domain, range, and asymptote. The domain is all real numbers, as the function is defined for any value of x. The range depends on the value of a, where f(x) > 0 if 0 < a < 1 and f(x) > 0 if a > 1. The function has a horizontal asymptote at y = 0 if 0 < a < 1 and y = ∞ if a > 1. Furthermore, we can identify whether the function is increasing or decreasing based on the value of a.
These examples demonstrate how to analyze different types of functions, but the process may vary for other types of functions, such as linear, logarithmic, or trigonometric functions. By understanding the properties and behaviors of functions, we can gain insights into their mathematical representation and solve various problems related to them.
Summary of 1.1-1.4 Analyzing Functions Answers
In this article, we have explored the concepts of analyzing functions and provided answers to exercises related to various aspects of function analysis. Here is a summary of the key concepts and answers:
1.1 Understanding Functions
- A function is a rule that assigns each input value to a unique output value.
- The domain of a function consists of all possible input values, and the range consists of all possible output values.
- The graphical representation of a function can help visualize its behavior.
1.2 Evaluating Functions
- To evaluate a function at a specific input value, substitute the input value into the function and simplify.
- Exponents, radicals, and rational expressions may require additional algebraic manipulations.
1.3 Analyzing Graphs of Functions
- The x-intercepts of a graph represent the input values where the function is equal to zero.
- The y-intercepts of a graph represent the output values when the input is equal to zero.
- The end behavior of a graph describes the behavior of the function as x approaches positive or negative infinity.
1.4 Interpreting Key Features of Graphs
- Local maximums and minimums represent points where the function reaches a high or low point relative to its immediate surroundings.
- Increasing and decreasing intervals describe the intervals where the function is respectively increasing or decreasing.
- Symmetry can help determine if a graph is symmetric with respect to the y-axis (even symmetry) or origin (odd symmetry).
By understanding these key concepts and using the provided answers to the exercises, you can effectively analyze functions and gain insights into their behavior, domains, ranges, and graphical representations. Remember to practice applying these concepts to various function examples to further strengthen your understanding.