
Understanding the concept of slope and perpendicular lines is crucial in the study of geometry and algebra. In this article, we will explore the answer key for the exercises in Section 10.2 of a textbook or workbook focused on this topic.
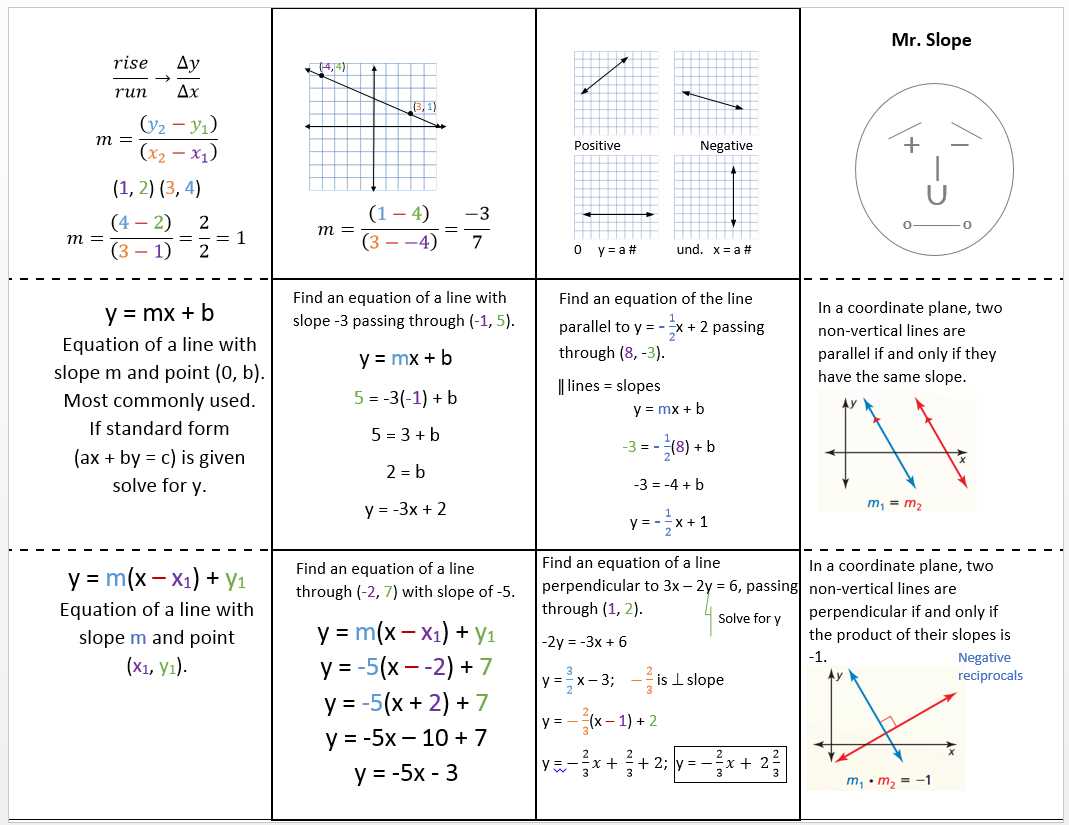
The concept of slope is a fundamental one in mathematics. It measures the steepness of a line and provides important information about its direction. The formula for calculating slope is “rise over run,” which means the change in y-coordinates divided by the change in x-coordinates.
In Section 10.2, students are likely to encounter various exercises that involve finding the slope of a line or determining whether two lines are perpendicular. These exercises may require the knowledge of the slope-intercept form of a linear equation, y = mx + b, where m represents the slope of the line.
When it comes to finding the answer key for these exercises, it is important to check that the calculations are correct and the reasoning behind the solutions is clear. It is also helpful to understand the properties of perpendicular lines, such as the fact that their slopes are negative reciprocals of each other.
By reviewing the answer key for Section 10.2, students can verify their own work, gain a deeper understanding of the concepts, and improve their problem-solving skills in the realm of slope and perpendicular lines.
Slope and Perpendicular Lines Answer Key
Understanding the concept of slope and perpendicular lines is crucial in mathematics and can be applied in various real-life situations. The answer key for slope and perpendicular lines helps students to verify their solutions and gain confidence in working with these concepts.
The slope of a line is a measure of its steepness and is calculated by dividing the change in the y-coordinates by the change in the x-coordinates. Using the answer key, students can check their calculations and ensure that they are finding the correct slopes for different lines.
Perpendicular lines are lines that intersect at a right angle. The answer key for perpendicular lines allows students to verify if their lines are indeed perpendicular by checking if the slopes of the two lines are negative reciprocals of each other. This step is important in geometry and algebraic problem-solving.
The answer key also provides additional practice problems that students can use to further reinforce their understanding of slope and perpendicular lines. By comparing their solutions with the answer key, students can identify any mistakes they may have made and learn from them.
In conclusion, the slope and perpendicular lines answer key is an essential tool for students learning about these concepts. It provides a way for students to check their solutions, gain confidence in their calculations, and identify areas for improvement. By using the answer key, students can enhance their understanding and mastery of slope and perpendicular lines.
The Basics of Slope
The concept of slope is fundamental in mathematics and is often used to describe the steepness or incline of a line. A line’s slope is a measure of how much it rises or falls over a given horizontal distance. Slope is represented by the letter “m” in equations and is calculated by dividing the change in y-coordinates by the change in x-coordinates between two points on the line.
In the slope-intercept form of a linear equation, y = mx + b, the slope (m) is the coefficient of x. It determines the direction and steepness of the line. A positive slope indicates an upward direction, while a negative slope indicates a downward direction. A slope of zero indicates a horizontal line, and an undefined slope indicates a vertical line.
To find the slope between two points (x1, y1) and (x2, y2), we can use the formula:
m = (y2 – y1) / (x2 – x1)
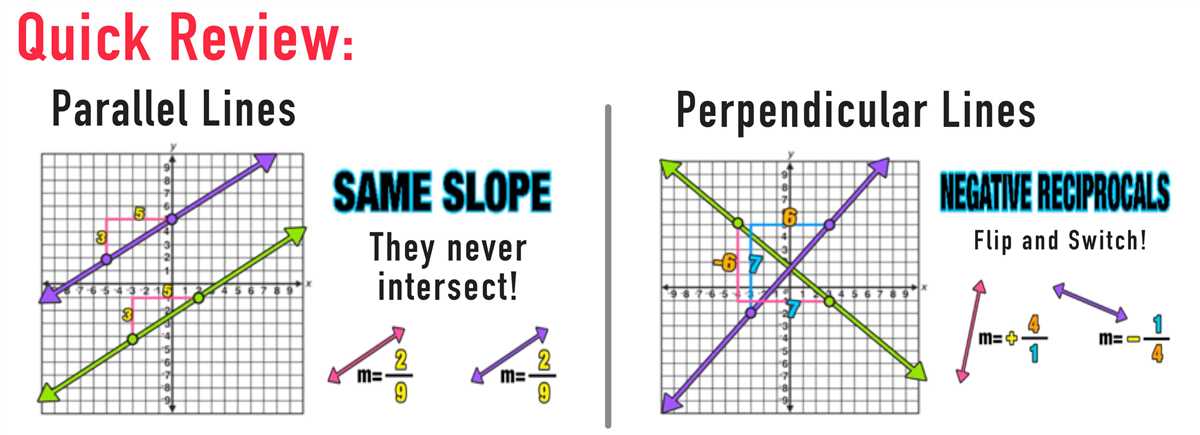
In addition to representing the incline of a line, slope has other important properties. Perpendicular lines have slopes that are negative reciprocals of each other. Parallel lines have the same slope. The slope can also be used to determine if a line is increasing or decreasing, and it can be used to find the equation of a line when given a point and the slope.
Understanding the basics of slope is essential for solving problems involving lines and understanding their characteristics. It is a fundamental concept that is used in various applications, including physics, engineering, and economics.
Calculating the Slope of a Line
The slope of a line is a fundamental concept in mathematics and physics. It describes the steepness or inclination of a line and can be calculated using different methods. The slope is represented by the letter m and is defined as the ratio of the change in y-coordinates (vertical change) to the change in x-coordinates (horizontal change) between two points on the line.
To calculate the slope of a line, you need two points that lie on the line. Let’s call these points (x1, y1) and (x2, y2). The formula for calculating the slope, m, is:
m = (y2 – y1) / (x2 – x1)
This formula tells us that to find the slope, we need to subtract the y-coordinate of the first point from the y-coordinate of the second point (vertical change) and divide it by the difference of their x-coordinates (horizontal change). The result will give us the slope of the line.
The slope of a line can be positive, negative, zero, or undefined. A positive slope indicates an upward inclination, a negative slope indicates a downward inclination, a zero slope indicates a horizontal line, and an undefined slope indicates a vertical line. By calculating the slope, we can determine the direction and steepness of a line and use this information in various mathematical and scientific applications.
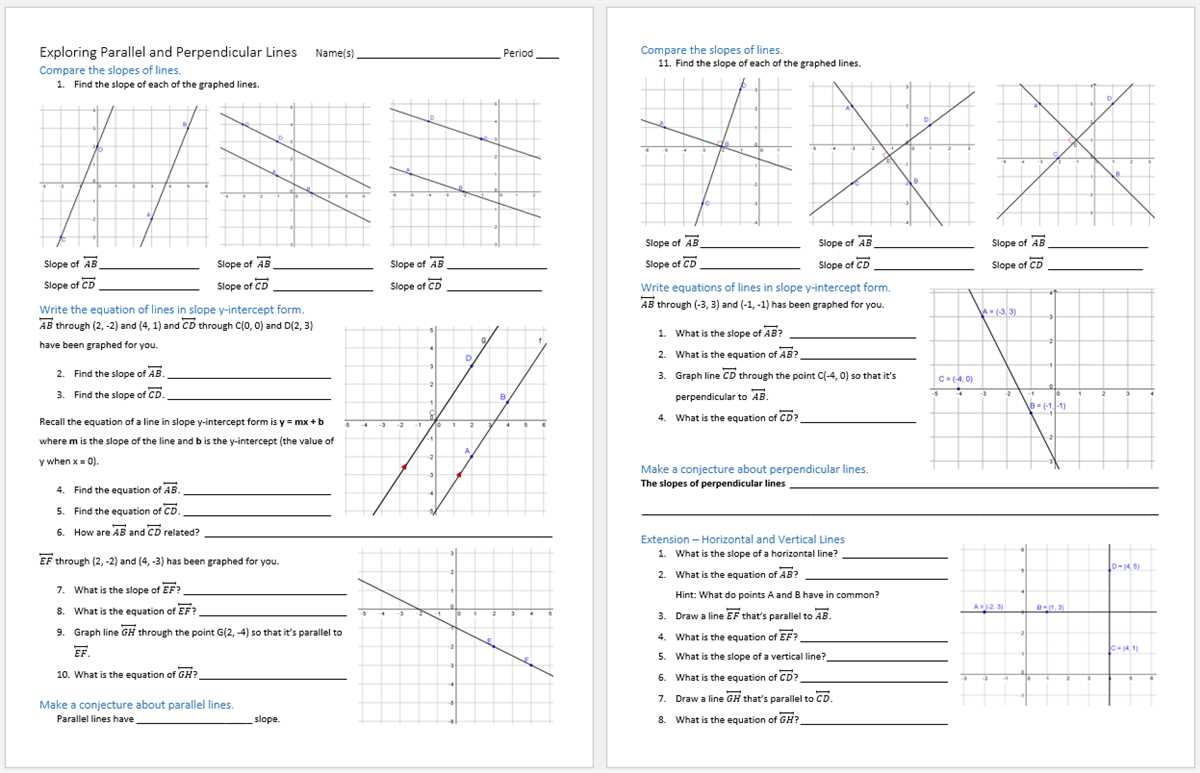
Determining if Lines are Parallel or Perpendicular

When working with lines in mathematics, it is important to be able to determine if two lines are parallel or perpendicular. This information can be crucial in solving various geometry and algebra problems. To determine if two lines are parallel or perpendicular, it is necessary to compare their slopes.
The slope of a line is a measure of how steep it is and can be calculated as the ratio of the change in y-coordinates to the change in x-coordinates. If two lines have the same slope, they are parallel. If the slopes are negative reciprocals of each other, the lines are perpendicular.
For example, consider the lines with the equations y = 2x + 3 and y = -1/2x + 5. The slope of the first line is 2, and the slope of the second line is -1/2. Since these slopes are negative reciprocals of each other, the lines are perpendicular.
To further illustrate this concept, a table can be created to compare the slopes of different lines. This table can help determine whether the lines are parallel or perpendicular based on their respective slopes. By analyzing the table, patterns can be identified, making it easier to determine the relationship between the lines.
Finding the Equation of a Line Perpendicular to Another
When given a line and asked to find the equation of a line perpendicular to it, there are several key steps to follow. Understanding these steps is essential in order to find the correct equation.
First, it is important to know that the slope of a line is a measure of its steepness. It can be calculated by comparing the change in y-coordinates to the change in x-coordinates. A line perpendicular to another will have a slope that is the negative reciprocal of the original line’s slope.
For example, if the original line has a slope of 2/3, the perpendicular line will have a slope of -3/2. This can be used as the starting point for finding the equation of the perpendicular line.
Once the perpendicular slope is determined, the next step is to find the equation in either point-slope form or slope-intercept form. Point-slope form is useful when a specific point on the line is given, whereas slope-intercept form is helpful when the y-intercept is known. Both forms can be used to find the equation of the perpendicular line, depending on the given information.
For point-slope form, the equation can be written as y – y1 = m(x – x1), where (x1, y1) is a point on the line and m is the slope. By substituting the values of the perpendicular slope and the given point, the equation can be simplified and solved for y.
In slope-intercept form, the equation can be written as y = mx + b, where m is the slope and b is the y-intercept. By substituting the values of the perpendicular slope and the known y-intercept, the equation can be simplified and solved for y.
By following these steps and understanding the relationship between slopes, it is possible to find the equation of a line perpendicular to another. Practice and repetition can help solidify this concept and make it easier to apply in different scenarios.
Solving Problems Involving Slope and Perpendicular Lines
When working with slope and perpendicular lines, it is important to understand the relationship between the two concepts. The slope of a line represents its steepness, while the concept of perpendicular lines relates to the angle formed between two intersecting lines. By combining these two ideas, we can solve various problems and analyze geometric figures.
One common problem involving slope and perpendicular lines is finding the equation of a line perpendicular to a given line. To solve this problem, we need to know the slope of the given line. The slope of a perpendicular line is the negative reciprocal of the slope of the given line. By using this information, we can write the equation of the perpendicular line in slope-intercept form.
Another problem that often arises is determining if two lines are perpendicular. To do this, we can compare the slopes of the two lines. If the slopes are negative reciprocals of each other, the lines are perpendicular. Otherwise, they are not. This can be useful in geometry problems involving triangles or other shapes, where perpendicular lines play a significant role.
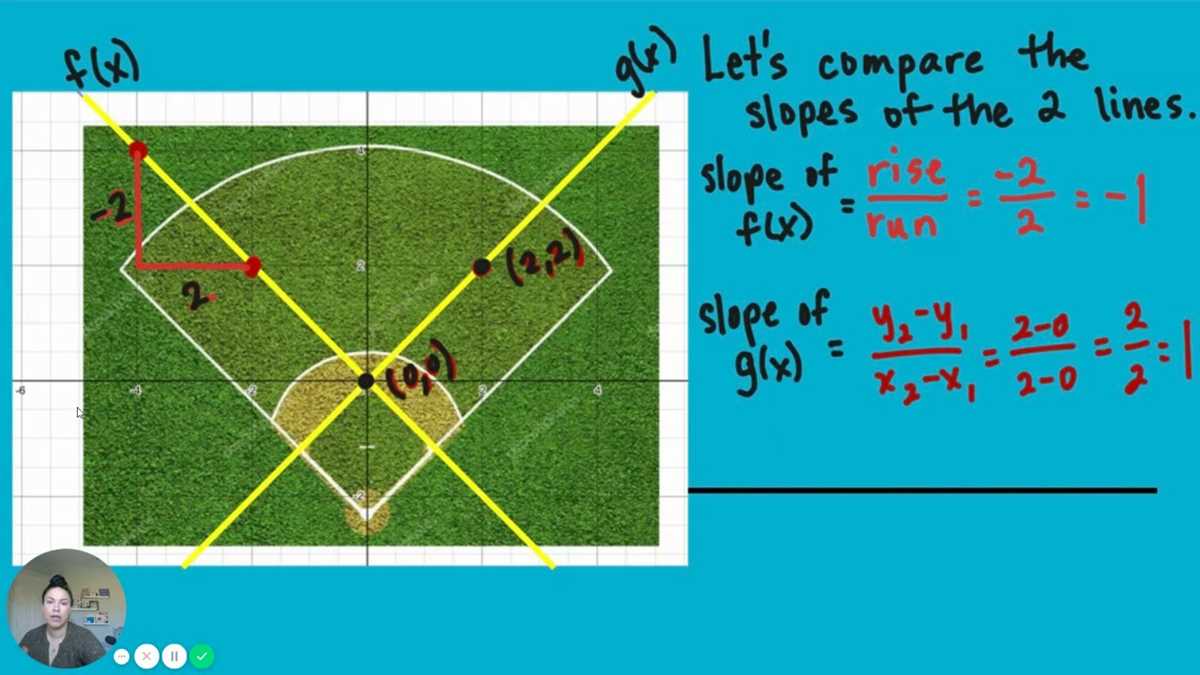
Furthermore, the concept of slope is essential for analyzing the rate of change in real-life situations. For example, if we are given a graph representing the distance traveled over time, the slope of the line represents the speed at which an object is moving. By understanding slope, we can analyze patterns, predict future behavior, and solve real-world problems.
In conclusion, solving problems involving slope and perpendicular lines requires a solid understanding of these concepts and their relationships. By using the formulas and relationships discussed, we can confidently solve problems related to finding equations, determining perpendicularity, and analyzing real-life situations. Mastering these skills is crucial for success in algebra, geometry, and beyond.
Practice Exercises and Answer Key
Here are some practice exercises to help reinforce your understanding of slope and perpendicular lines. Try to solve each exercise on your own before referring to the answer key below.
Exercise 1:
Find the slope of the line passing through the points (2, 4) and (6, 10).
Exercise 2:
Find the equation of the line that passes through the point (3, -2) and has a slope of 2.
Exercise 3:
Find the equation of the line that is perpendicular to the line y = 3x + 2 and passes through the point (1, -4).
Answer Key:
- Exercise 1: The slope of the line is 2.
- Exercise 2: The equation of the line is y = 2x – 8.
- Exercise 3: The equation of the line is y = -1/3x – 7/3.
Remember to practice these exercises multiple times to become comfortable with the concepts. Understanding slope and perpendicular lines will be useful in various mathematical and real-world applications.