When studying geometry, one concept that often comes up is that of inscribed triangles and quadrilaterals. In geometry, an inscribed shape is one that is drawn inside another shape in such a way that its vertices lie on the edges of the larger shape. This concept is particularly important when working with circles, as inscribed shapes can provide valuable information about the properties and relationships within the circle.
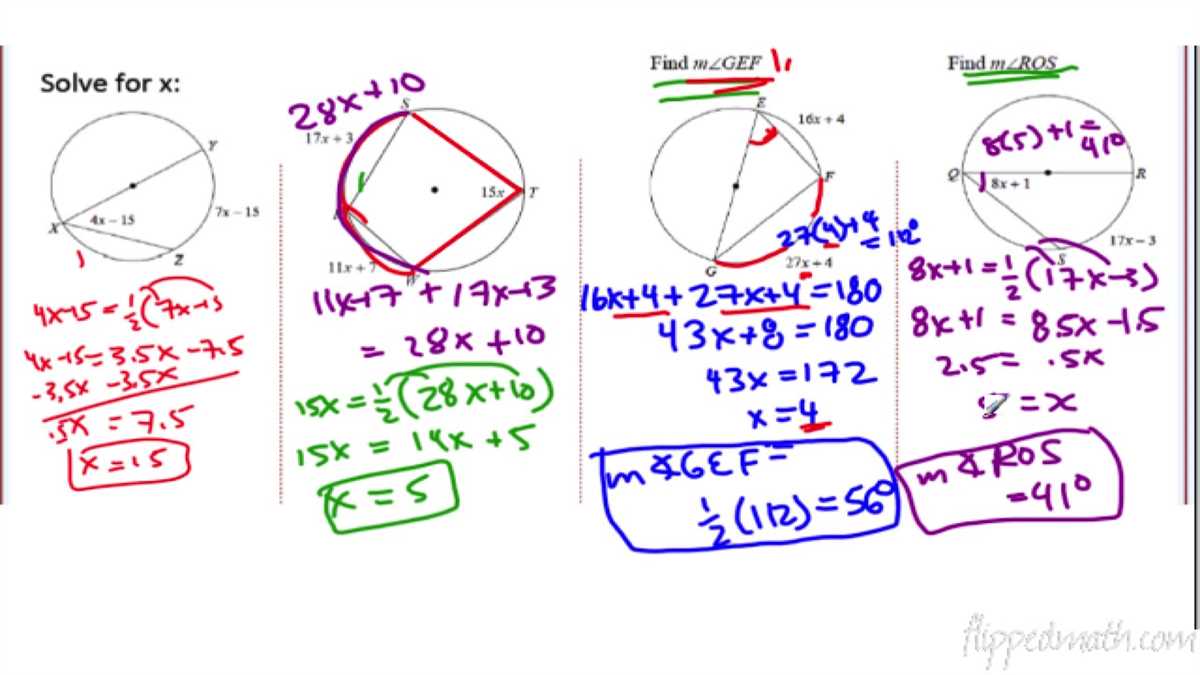
One key question when working with inscribed triangles and quadrilaterals is how to find the measures of their angles. Fortunately, there is a theorem – known as the Inscribed Angle Theorem – that provides a way to find these measures. According to this theorem, the measure of an inscribed angle is half the measure of the intercepted arc.
Additionally, inscribed triangles and quadrilaterals can also provide insights into the relationships between angles and line segments. For example, in an inscribed triangle, the opposite angles are supplementary, meaning that their measures add up to 180 degrees. In an inscribed quadrilateral, opposite angles are also supplementary, and the opposite sides are congruent.
Overall, understanding the properties and relationships of inscribed triangles and quadrilaterals is essential in the study of geometry. By knowing how to find the measures of angles and the relationships between angles and line segments, students can confidently solve problems related to inscribed shapes and effectively analyze the properties of circles.
Insights into 12.1 Inscribed Triangles and Quadrilaterals Answer Key
Inscribed triangles and quadrilaterals are figures that are contained within a circle where each of their vertices lies on the circumference of the circle. In the context of the 12.1 Inscribed Triangles and Quadrilaterals Answer Key, this topic explores the properties and relationships of these special geometric shapes.
One key insight provided in the answer key is that the sum of the measures of the angles in an inscribed triangle is always 180 degrees. This property, known as the Angle Sum Theorem for Inscribed Triangles, can be utilized to solve various problems involving these triangles. It allows us to determine the measure of one angle if the measures of the other two angles are known.
The answer key also delves into the relationships between angles formed by inscribed quadrilaterals. One notable relationship is that the opposite angles in an inscribed quadrilateral are supplementary, meaning they add up to 180 degrees. This property, known as the Opposite Angles Theorem for Inscribed Quadrilaterals, can be used to find the measure of one angle if the measure of its opposite angle is known.
In addition to angle relationships, the answer key may provide insights into other properties of inscribed triangles and quadrilaterals. These properties may include the lengths of their sides, the relationships between their sides and angles, or the measurements of their arcs and chords.
To best understand and apply the concepts related to inscribed triangles and quadrilaterals, it is important to thoroughly review the 12.1 Inscribed Triangles and Quadrilaterals Answer Key. By doing so, students can develop a solid understanding of the topic and successfully solve problems involving these geometric shapes.
Understanding Inscribed Triangles and Quadrilaterals

Inscribed triangles and quadrilaterals are geometric figures that are formed when their vertices lie on the circumference of a circle. These shapes have unique properties and can be used to solve various mathematical problems.
Inscribed Triangles: An inscribed triangle is a triangle whose vertices are located on the circumference of a circle. One of the key properties of an inscribed triangle is that the angle subtended by any side at the center of the circle is double the angle subtended by the same side at the circumference. This property, known as the Inscribed Angle Theorem, can be used to solve problems involving angles in inscribed triangles.
For example, if we are given an inscribed triangle with one side length and two angles, we can use the Inscribed Angle Theorem to find the remaining angles of the triangle.
Inscribed Quadrilaterals: An inscribed quadrilateral is a quadrilateral whose vertices are located on the circumference of a circle. One of the important properties of an inscribed quadrilateral is that opposite angles are supplementary. This means that the sum of the measures of two opposite angles is always 180 degrees.
For example, if we know the measure of one angle in an inscribed quadrilateral, we can use the property of supplementary angles to find the measure of the opposite angle.
Understanding the properties and characteristics of inscribed triangles and quadrilaterals is crucial in solving problems involving circles and circular arcs. These figures provide a deeper insight into the relationships between angles and sides in a circle, and can be used to prove various geometric theorems and solve complex mathematical problems.
Key Concepts and Definitions
In the study of inscribed triangles and quadrilaterals, there are several key concepts and definitions that are important to understand. These concepts and definitions provide the foundation for understanding the properties and relationships of inscribed shapes.
1. Inscribed Triangle:
An inscribed triangle is a triangle whose vertices lie on the circumference of a circle. In other words, all three points of the triangle are on the circle.
2. Inscribed Quadrilateral:
An inscribed quadrilateral is a quadrilateral whose four vertices lie on the circumference of a circle. Like the inscribed triangle, all four points of the quadrilateral are on the circle.
3. Central Angle:
A central angle is an angle whose vertex is at the center of the circle. The measure of a central angle is equal to the measure of the arc it intercepts on the circumference of the circle.
4. Inscribed Angle:
An inscribed angle is an angle whose vertex is on the circumference of the circle and whose sides intersect the circle. The measure of an inscribed angle is half the measure of the intercepted arc.
5. Intercepted Arc:
The intercepted arc is the portion of the circle’s circumference that is “cut off” or intercepted by the inscribed angle. The measure of the intercepted arc is equal to twice the measure of the inscribed angle.
6. Tangent:
A tangent is a line that intersects a circle at exactly one point, known as the point of tangency. The tangent is perpendicular to the radius that connects the point of tangency to the center of the circle.
By understanding and applying these key concepts and definitions, one can analyze and solve problems involving inscribed triangles and quadrilaterals.
Properties of Inscribed Triangles
Inscribed triangles are triangles that are contained within a circle in such a way that all three vertices of the triangle lie on the circumference of the circle. This special arrangement of the triangle and the circle leads to several interesting properties.
1. Inscribed Angle: One of the most important properties of inscribed triangles is that the measure of an angle inscribed in a circle is half the measure of the intercepted arc. This means that if angle ABC is an inscribed angle and arc ACB is the intercepted arc, then the measure of angle ABC is equal to half the measure of arc ACB.
2. Inscribed Triangle Theorem: Another key property of inscribed triangles is known as the Inscribed Triangle Theorem. This theorem states that if two chords intersect inside a circle, then the products of their segments are equal. In other words, if chords AB and CD intersect at point E, then AE · EB = CE · ED.
3. Right Triangle Property: Inscribed triangles can also have special properties related to the angles of the triangle. For example, if one angle of an inscribed triangle is a right angle, then the triangle is called a right triangle. This property is derived from the fact that the diameter of a circle is perpendicular to any chord that passes through its midpoint.
These properties of inscribed triangles can be utilized to solve various geometric problems and prove other mathematical theorems. The understanding of these properties is fundamental in the study of circles and their associated geometrical relationships.
Properties of Inscribed Quadrilaterals
When a quadrilateral is inscribed in a circle, it has several interesting properties that can be used to solve problems involving its angles and sides.
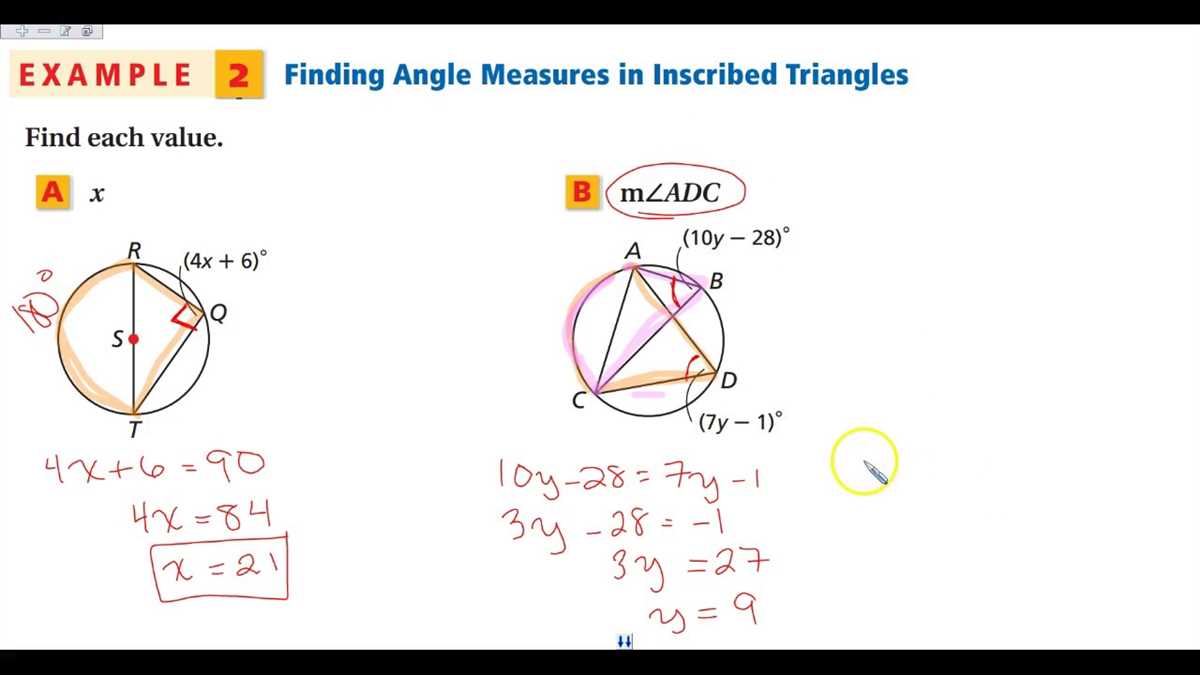
One property of an inscribed quadrilateral is that the opposite angles are supplementary. In other words, the sum of the measures of the two opposite angles of the quadrilateral is equal to 180 degrees. This property can be used to find the measure of an unknown angle in the quadrilateral if the measures of the other three angles are known.
Another property of an inscribed quadrilateral is that the opposite sides are equal in length. This means that if we know the length of one side of the quadrilateral, we can determine the lengths of the other three sides. This property can be particularly useful when we need to find the perimeter of the quadrilateral.
Example:
Consider a quadrilateral inscribed in a circle with side lengths AB = 4 cm, BC = 6 cm, CD = 5 cm. To find the length of side DA, we can use the property that opposite sides in an inscribed quadrilateral are equal. Since AB and CD are opposite sides, and their lengths are known to be 4 cm and 5 cm respectively, we can conclude that DA is also 5 cm.
In addition to these properties, inscribed quadrilaterals can also have other special relationships, such as the diagonals of the quadrilateral intersecting at right angles, or the diagonals bisecting each other. These relationships can be helpful when solving more complex problems involving inscribed quadrilaterals.
Solving Problems Involving Inscribed Triangles and Quadrilaterals
When dealing with inscribed triangles and quadrilaterals, it is important to understand the relationship between the angles and sides of these shapes. By using various properties and theorems, we can solve problems involving inscribed triangles and quadrilaterals.
One key property to remember is that the opposite angles of an inscribed quadrilateral add up to 180 degrees. This property allows us to find missing angles in a quadrilateral by subtracting the known angles from 180 degrees.
To find missing side lengths in an inscribed triangle or quadrilateral, we can use the Pythagorean theorem. This theorem states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. By applying this theorem, we can solve for the missing side lengths.
Another important concept to understand is the relationship between angles and arcs in a circle. The measure of an inscribed angle is equal to half the measure of its intercepted arc. This relationship allows us to find missing angles by setting up equations with the measure of the intercepted arcs.
In summary, when solving problems involving inscribed triangles and quadrilaterals, it is crucial to understand the properties and relationships between angles, sides, and arcs. By applying these properties and using theorems such as the Pythagorean theorem, we can effectively solve problems and find missing angles and side lengths in inscribed shapes.