
When working with absolute value functions, it is important to understand their attributes and how they affect the graph. In this practice exercise, we will explore some key attributes of absolute value functions and provide an answer key to help you check your work.
One of the main attributes of absolute value functions is their “v-shape” graph. The graph of an absolute value function resembles the letter “v” and is symmetric with respect to the y-axis. This means that any point (x, y) on the graph has a corresponding point (-x, y) that is also on the graph. This symmetry is important to keep in mind when graphing or analyzing absolute value functions.
Another important attribute of absolute value functions is the vertex. The vertex is the point where the graph changes direction and is located at the minimum or maximum value of the function. For example, the graph of the function f(x) = |x – 3| has a vertex at (3, 0), where the graph changes direction from decreasing to increasing. This vertex provides valuable information about the overall shape and behavior of the function.
When solving equations involving absolute value functions, it is essential to consider the two possible solutions. Absolute value functions can have two solutions because the absolute value of a number is always positive. For example, when solving the equation |x – 3| = 5, we consider both x – 3 = 5 and x – 3 = -5 as possible solutions. This concept is important to remember when determining the solutions to equations involving absolute value functions.
Understanding Absolute Value Functions and Their Attributes
Introduction
When studying mathematical functions, one important type to consider is the absolute value function. Absolute value functions are used to represent the distance between a point and the origin on the number line. They have a distinct “V” shape when graphed and possess several key attributes that are essential to understand.
Absolute Value
To start, it is crucial to grasp the concept of absolute value itself. The absolute value of a number is its distance from zero on the number line, regardless of its sign. For example, the absolute value of 5 is 5, and the absolute value of -5 is also 5. It is represented by vertical bars enclosing the number, like |x|.
Graph of an Absolute Value Function
When graphing an absolute value function, the resulting graph has a distinctive V shape. The vertex of the V represents the minimum or maximum value of the function, depending on whether the absolute value function is positive or negative. This vertex is located at the point (h, k), where the values h and k can be determined from the equation of the function.
Furthermore, the graph of an absolute value function is symmetric with respect to the vertical line passing through the vertex. This means that if a point (x, y) lies on the graph, then the point (-x, y) also lies on the graph. This symmetry helps in plotting points and understanding the overall shape of the function.
Attributes of Absolute Value Functions
Several key attributes define an absolute value function. First, the domain of an absolute value function is all real numbers, as the function is defined for any value of x. However, the range is bounded by a minimum or maximum value, depending on the function’s coefficient.
Additi
Definition of Absolute Value Functions
An absolute value function is a type of mathematical function that is defined by the absolute value of a variable. It is commonly denoted by the symbol |x|, where x represents the variable. The absolute value of a number is its distance from zero on a number line.
The absolute value function can be defined by the following equation:
f(x) = |x|
This equation means that the function f(x) is equal to the absolute value of the variable x. The absolute value function takes any real number as input and returns its non-negative value. For positive numbers, the function returns the same value, while for negative numbers, it returns the positive value. Therefore, the absolute value function effectively “removes” the negative sign from a number.
Graphically, the absolute value function is represented by a V-shaped graph. The vertex of the graph is at the point (0,0), and the axis of symmetry is the vertical line x = 0. The function is increasing to the right of the vertex and decreasing to the left. The graph reflects across the x-axis to represent the absolute value function for negative values.
The absolute value function has several important properties, including symmetry, non-negativity, and piecewise definition. By understanding and analyzing these properties, mathematicians can solve equations, graph functions, and make predictions about real-world phenomena.
Graphical Representation of Absolute Value Functions
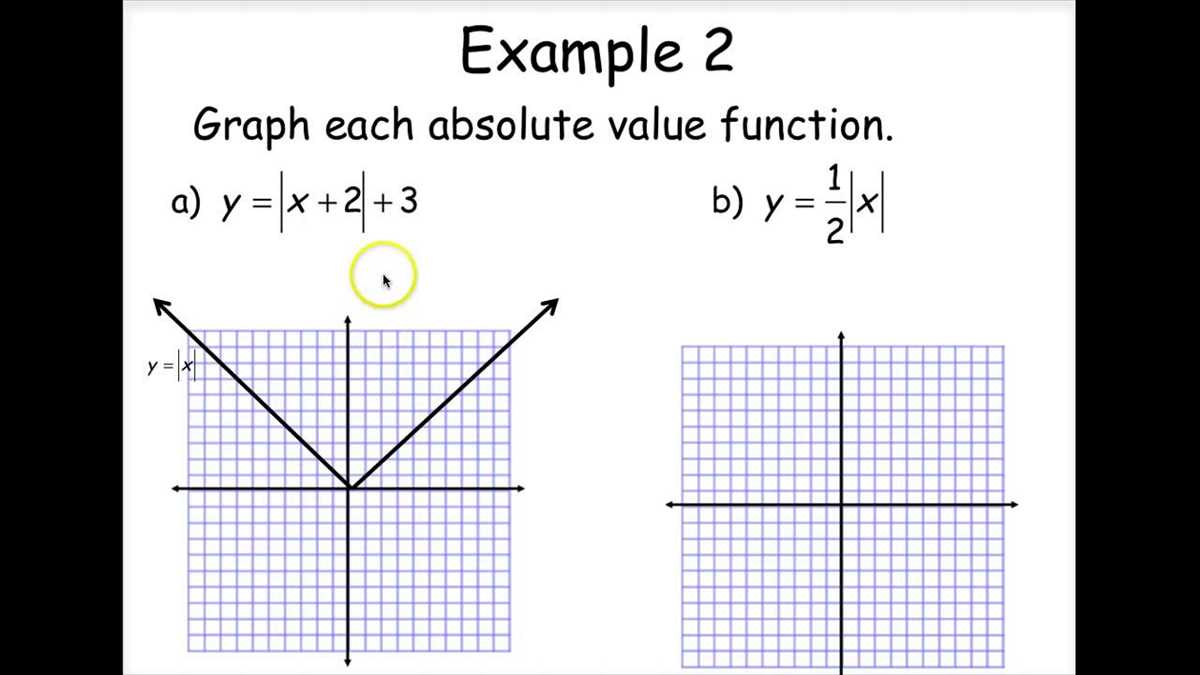
Absolute value functions are a type of mathematical function that has a distinct graphical representation. The graph of an absolute value function takes the shape of a “V” or an inverted “V” depending on the coefficient of the absolute value expression.
The graph of an absolute value function can be divided into two parts: the left side and the right side. On the left side of the graph, the function mirrors the right side of the graph, but reflects it across the y-axis. This is due to the property of absolute value, which ensures that the output of the function is always positive.
The vertex of the graph, which is the lowest or highest point on the graph, depending on whether the function opens up or down, can be used to determine important attributes of the function. The x-coordinate of the vertex represents the value of x that produces the minimum or maximum value of the function.
The steepness of the “V” shape of the graph is determined by the coefficient of the absolute value expression. A larger coefficient leads to a steeper graph, while a smaller coefficient leads to a gentler slope. This coefficient also affects the width of the “V” shape, with larger coefficients resulting in narrower graphs and smaller coefficients resulting in wider graphs.
Summary:
- Absolute value functions have a “V” or inverted “V” shape graph.
- The left side of the graph mirrors the right side, but reflects across the y-axis.
- The vertex of the graph represents the minimum or maximum value of the function.
- The coefficient of the absolute value expression determines the steepness and width of the graph.
Characteristics of Absolute Value Functions
Absolute value functions are a type of mathematical function that have distinct characteristics and properties. These functions can be represented by the equation f(x) = |x|, where |x| denotes the absolute value of x. Understanding the key attributes of absolute value functions is essential for effectively analyzing and graphing them.
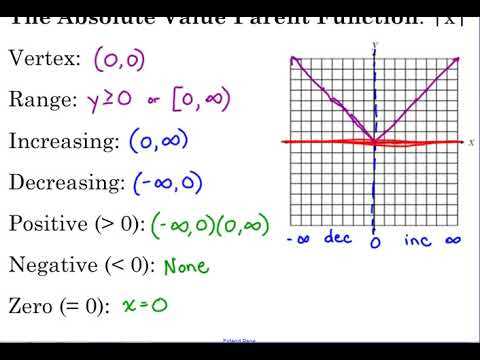
1. Symmetry: One of the defining characteristics of absolute value functions is their symmetry. The graph of an absolute value function is symmetric with respect to the y-axis. This means that if you reflect one side of the graph over the y-axis, you will obtain the other side.
2. Vertex: The vertex of an absolute value function is the point where the graph changes direction. It is the lowest or highest point on the graph, depending on whether the coefficient of x in the equation is positive or negative. The vertex of the function f(x) = |x| is (0, 0).
3. Rate of change: The rate of change of an absolute value function is constant, but it can be different on different intervals. The rate of change on the left side of the graph is negative, while on the right side it is positive. This means that the graph of an absolute value function increases or decreases linearly.
4. Range and domain: The range of an absolute value function is all non-negative real numbers, starting from 0. On the other hand, the domain is all real numbers. This means that the function is defined for all values of x.
5. Horizontal and vertical shifts: Just like other functions, absolute value functions can be shifted horizontally or vertically. A change in the equation of an absolute value function can result in a shift of the graph to the left or right, or up or down.
Understanding these characteristics of absolute value functions is crucial for effectively solving problems and analyzing real-world situations. By recognizing the patterns and properties of absolute value functions, it becomes easier to interpret their graphs and make accurate predictions.
Solving Equations and Inequalities Involving Absolute Value Functions
Absolute value functions are mathematical expressions that represent the distance of a number from zero on the number line. They are commonly used to solve equations and inequalities in various mathematical contexts.
When solving equations involving absolute value functions, there are two possible cases to consider: when the expression inside the absolute value is positive and when it is negative.
Case 1: Expression inside absolute value is positive
In this case, the equation or inequality simplifies to a simple algebraic expression. We can remove the absolute value symbols and solve for the variable using basic algebraic operations. The resulting solution will be a single value.
Case 2: Expression inside absolute value is negative
In this case, we need to change the sign of the expression inside the absolute value to make it positive. This can be done by multiplying the expression by -1. After removing the absolute value symbols, we solve the resulting equation or inequality using algebraic techniques, similar to Case 1. The resulting solution will also be a single value.
It is important to note that when solving inequalities involving absolute value functions, there may be multiple solutions. In these cases, we represent the solutions using interval notation or by creating a number line diagram.
In summary, solving equations and inequalities involving absolute value functions requires understanding and applying the rules and properties of absolute value. By considering the cases when the expression inside the absolute value is positive or negative, we can find the solutions to these mathematical expressions.
Analyzing Transformations of Absolute Value Functions
When analyzing absolute value functions, it is important to consider the transformations that can affect the shape and position of the graph. These transformations include shifts, stretches or compressions, and reflections. By understanding these transformations, we can accurately describe and graph absolute value functions.
One of the most basic transformations is the shift or translation of the graph. This can be described using the equation y = |x – h| + k, where (h, k) represents the coordinates of the vertex. A positive value of h would indicate a shift to the right, while a negative value would indicate a shift to the left. Similarly, a positive value of k would result in an upward shift, and a negative value would result in a downward shift.
Another transformation that can occur is a stretch or compression of the graph. This affects the steepness of the slopes of the graph. If the absolute value function has the form y = a|x – h| + k, where a is a constant, a value greater than 1 for a would result in a stretch, making the graph steeper. On the other hand, a value between 0 and 1 for a would result in a compression, making the graph flatter.
Finally, a reflection can also be applied to the graph of the absolute value function. This is achieved by negating the value of the x inside the absolute value function, resulting in y = |-(x – h)| + k. This reflection would result in the graph being mirrored over the y-axis.
By understanding and combining these transformations, we can create accurate representations of absolute value functions and analyze their attributes. These attributes include the vertex (h, k), the slope of the graph, and the x-intercepts. The vertex is a key point on the graph that determines the location of the minimum or maximum point. The slope of the graph provides information about the steepness of the slopes, and the x-intercepts represent the points where the graph intersects the x-axis.
Overall, analyzing and understanding the transformations of absolute value functions enables us to accurately describe and graph these functions, as well as identify their key attributes. This knowledge is essential for solving problems and real-world applications involving absolute value functions.
Real-Life Applications of Absolute Value Functions
Absolute value functions are not just abstract concepts in mathematics; they have many real-life applications. Here are a few examples:
1. Distance and Displacement
Absolute value functions are frequently used in physics to calculate distance and displacement. The absolute value of a number represents its magnitude without regard to its sign. When calculating the distance between two points, the absolute value function can be used to eliminate the negative sign, resulting in an accurate measurement of the physical distance.
2. Temperature
Absolute value functions are also applicable to temperature measurements. Temperature can be expressed as a positive or negative value depending on the scale used. However, when calculating the difference between two temperatures, the absolute value function is employed to ignore the negative sign and provide an accurate representation of the temperature change.
3. Finance
In finance, absolute value functions are used to analyze and compare financial data. For example, when calculating the rate of return on an investment, the absolute value function is utilized to ensure that the percentage change is always positive, regardless of whether the investment yielded a profit or a loss.
In conclusion, absolute value functions have diverse and practical applications in various fields, including physics, temperature measurement, and finance. They provide a straightforward method for determining distances, calculating temperature changes, and analyzing financial data. By understanding and utilizing absolute value functions, individuals can make more accurate measurements and calculations in their daily lives.