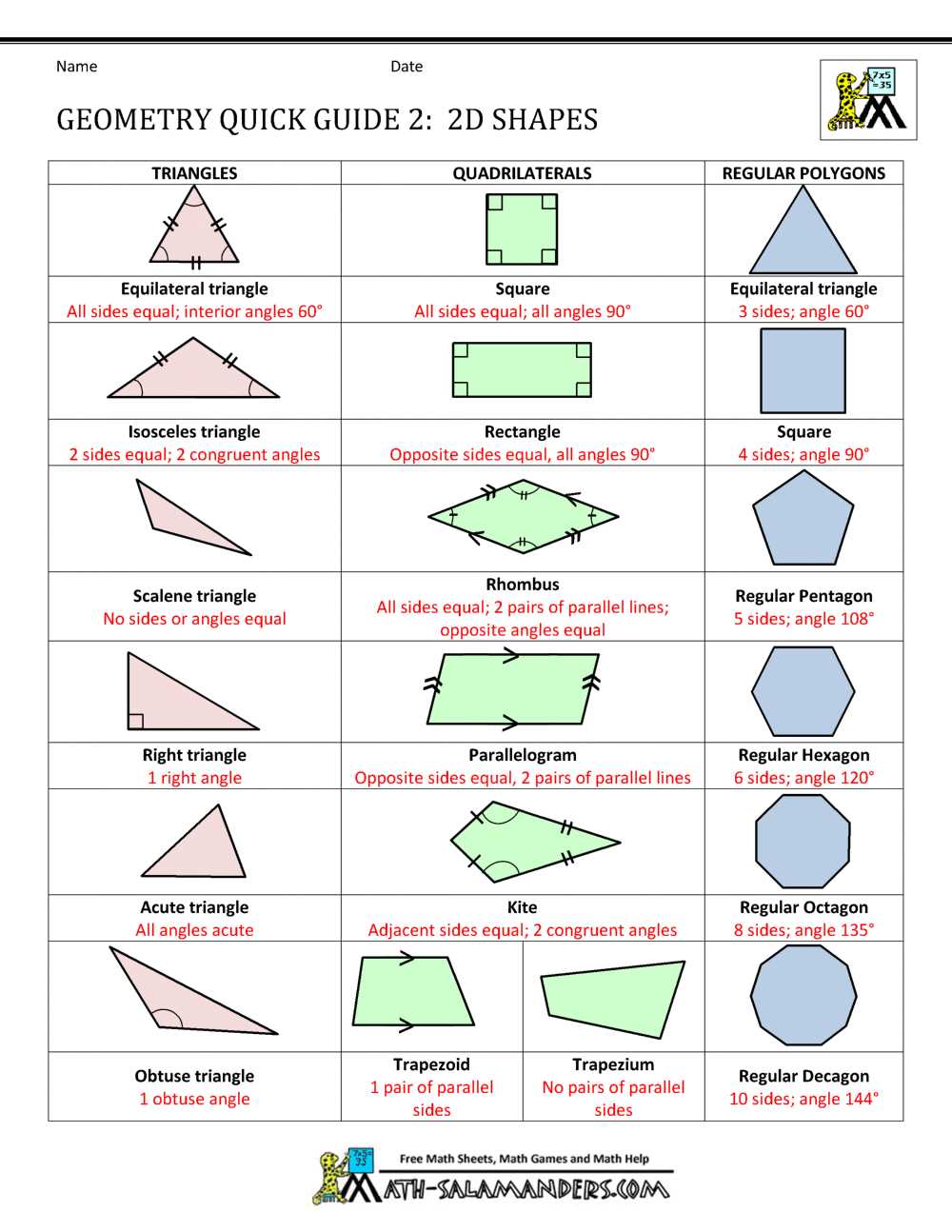
Geometry is a fascinating branch of mathematics that explores the properties and relationships of shapes in two and three dimensions. It is a fundamental subject that can be found in various aspects of our daily lives, from the buildings we inhabit to the objects we interact with.
When studying geometry, one comes across a multitude of concepts, ranging from lines and angles to polygons and solid figures. These concepts serve as the building blocks for understanding the intricacies of the geometric world. In order to fully comprehend these concepts, one must be able to solve a variety of problems and find precise answers.
In this article, we will delve into the realm of 2.4 geometry answers. This particular section focuses on solving problems related to the measurement of angles and the classification of triangles. By providing step-by-step solutions and explanations, we hope to assist students and enthusiasts alike in their journey to master the intricacies of geometry.
Overview of Geometry Answers

Geometry is a branch of mathematics that deals with the study of shapes, sizes, and properties of figures. It is an important subject that forms the foundation for various scientific and engineering disciplines. In geometry, students are often required to solve problems and provide answers based on their understanding of geometric concepts and principles.
Geometry answers can be found by applying various techniques and formulas. Students need to have a solid grasp of fundamental concepts such as points, lines, angles, and shapes. They should also possess knowledge of more advanced topics like congruence, similarity, and the Pythagorean theorem. By applying these concepts and principles, students can solve problems related to perimeter, area, volume, and other geometric measurements.
One common type of geometry problem involves finding missing angles in a given figure. This can be accomplished using the properties of angles formed by parallel lines and transversals, or by applying trigonometric ratios in right triangles. Another type of problem is determining the length of a side or the area of a shape. This often requires the use of formulas specific to the given figure, such as the formula for the area of a circle or the Pythagorean theorem for right triangles.
When providing geometry answers, it is important to show the steps taken to arrive at the solution. This helps to demonstrate understanding and ensures accuracy. Additionally, it is essential to include units of measurement where applicable, as this provides context and clarity to the answer. The use of diagrams, tables, and visual aids can also be helpful in presenting geometry answers.
Overall, geometry answers require a combination of understanding of geometric principles, problem-solving skills, and the application of relevant formulas. With practice and a solid foundation in geometry, students can become proficient in finding accurate and comprehensive answers to various geometric problems.
Importance of Geometry Answers in Education
In the field of education, geometry is an essential branch of mathematics that deals with the study of shapes, sizes, and properties of objects. It plays a crucial role in developing students’ logical thinking and problem-solving skills. To assess their understanding and mastery of geometry concepts, geometry answers are of utmost importance. These answers allow educators to evaluate students’ comprehension of the subject and provide feedback for further improvement.
Geometry answers act as a tool for assessment and evaluation. By solving geometry problems and providing answers, students demonstrate their understanding of the geometric principles and concepts. Educators can use these answers to assess students’ reasoning abilities and mathematical thinking. It helps in identifying areas where students might need additional support and guidance. Moreover, geometry answers provide a benchmark for grading and evaluating students’ performance in the subject.
Additionally, geometry answers promote critical thinking and problem-solving skills. Geometry involves visualizing and manipulating shapes and figures, which requires logical reasoning and analytical thinking. By finding solutions and providing answers to geometry questions, students learn how to approach complex problems systematically and creatively. This skill set is not only valuable in mathematics but also in various real-life scenarios where logical thinking and problem-solving are essential.
Furthermore, geometry answers foster self-assessment and self-improvement. When students check their answers against the given solutions, they can identify their mistakes and areas of weakness. This self-assessment allows them to reflect on their understanding of the subject and take corrective measures to improve. Geometry answers provide a valuable feedback mechanism for students to gauge their progress and track their learning journey.
- Conclusion:
In conclusion, geometry answers play a significant role in education by providing a means for assessment, fostering critical thinking, and promoting self-assessment. They are an essential tool for educators to evaluate students’ understanding and mastery of geometry concepts. By actively engaging in solving geometry problems and providing answers, students develop important skills that are valuable not only in mathematics but also in real-life scenarios.
Understanding the Basics: Geometry Answer Key
Geometry is a branch of mathematics that deals with the properties and relationships of geometric figures in space. It is essential to have a solid understanding of the basic concepts in geometry in order to solve problems effectively. Here, we provide an answer key that will help you check your answers and enhance your understanding of the subject.
When studying geometry, it is important to be familiar with key terms and definitions. For example, a line is a straight path that extends indefinitely in both directions, while a line segment is a portion of a line that has two distinct endpoints. Understanding these terms is crucial when solving problems involving lines and line segments.
Basic Geometric Shapes:
- A point is a location in space. It has no size or shape.
- A line is a straight path that extends infinitely in both directions.
- A line segment is a portion of a line with two endpoints.
- An angle is formed by two rays or line segments that share a common endpoint.
- A triangle is a polygon with three sides and three angles.
- A circle is a curve that is equidistant from a fixed center point.
Once you have a good grasp of the basic shapes and terminology, you can start solving more complex problems. The answer key provided will guide you through various exercises, such as finding missing angles in triangles, calculating the perimeter and area of polygons, and determining the volume of three-dimensional shapes.
Remember, practice is key when it comes to mastering geometry. By working through the answer key and practicing regularly, you will build a strong foundation in geometry and be able to confidently tackle more advanced concepts and problems.
Solving Geometric Problems with Geometry Answer Sheets
Solving geometric problems can be challenging and time-consuming, but with the help of geometry answer sheets, it becomes easier to understand and solve complex mathematical equations. Geometry answer sheets provide a comprehensive set of solutions and explanations for various geometric problems, allowing students to check their answers and learn from their mistakes.
Geometry answer sheets are designed to cover a wide range of topics, including angles, triangles, circles, polygons, and three-dimensional figures. Each answer sheet contains step-by-step solutions, formulas, and diagrams that help students visualize and understand the concepts involved. This not only improves their problem-solving skills but also enhances their overall understanding of geometry.
One of the key advantages of using geometry answer sheets is that they provide immediate feedback to students. By comparing their answers with the solutions provided, students can quickly identify any errors or misconceptions they might have. This feedback helps them to correct their mistakes and reinforces their understanding of the underlying principles.
Another benefit of geometry answer sheets is that they can be used as a study resource. Students can refer to these answer sheets while reviewing for exams or working on practice problems. This allows them to reinforce their knowledge and make sure they have mastered the necessary concepts before test day.
In conclusion, geometry answer sheets are an invaluable tool for students studying geometry. They provide clear and concise solutions to a wide range of geometric problems, help students identify and correct their mistakes, and serve as a valuable study resource. With the help of geometry answer sheets, students can improve their problem-solving skills and achieve success in their geometry studies.
Common Errors in Geometry Answers
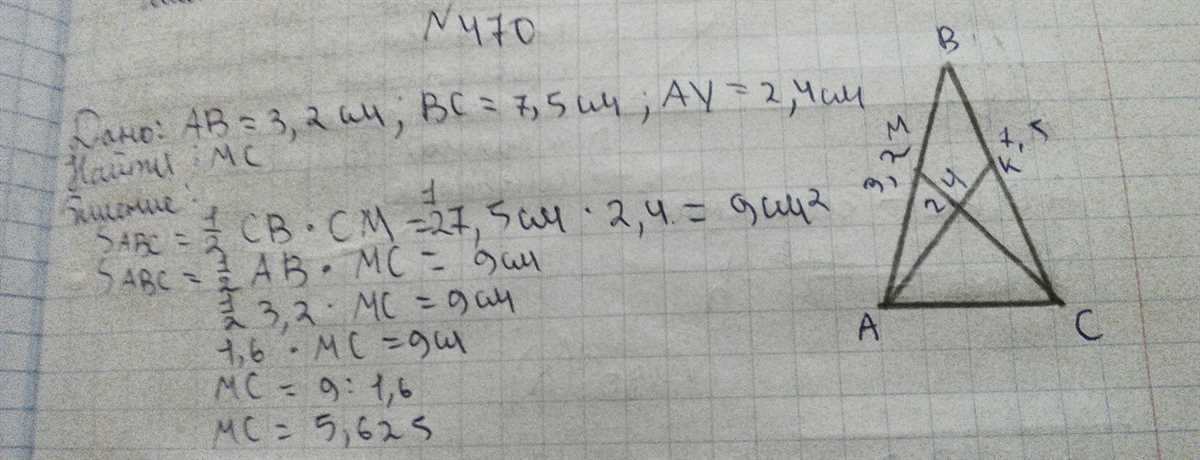
In the study of geometry, it is common for students to make errors when providing answers to problems. These errors can range from simple mistakes in calculation to misunderstandings of geometric concepts. By identifying and understanding these common errors, students can improve their geometry skills and achieve more accurate answers.
1. Misidentifying geometric figures:
- One common error is misidentifying geometric figures. For example, students may mistake a rectangle for a square or a parallelogram for a trapezoid. This can lead to incorrect solutions and a misunderstanding of the properties and relationships between different shapes.
- To avoid this error, students should carefully review the definitions and properties of geometric figures before attempting to solve problems. It is important to pay attention to the number of sides, angles, and other defining characteristics of each figure.
2. Incorrectly applying geometric formulas:
- Another common error is incorrectly applying geometric formulas. For instance, students may use the wrong formula to calculate the area of a triangle or the volume of a cylinder.
- To prevent this error, students should familiarize themselves with the correct formulas for different geometric calculations. It is also important to double-check the given information and ensure that the formula being used matches the problem at hand.
3. Failing to provide sufficient justification or explanation:
- One significant error in geometry answers is the failure to provide sufficient justification or explanation for the steps taken to arrive at the answer. Simply providing the final numerical result without showing the reasoning can lead to a loss of points and an incomplete understanding of the concepts.
- To avoid this error, students should make sure to include clear and concise explanations for each step. This can involve citing relevant theorems, postulates, or properties, as well as providing logical reasoning for any deductions or conclusions made during the problem-solving process.
By being aware of these common errors and taking steps to avoid them, students can improve their accuracy and understanding in geometry. Regular practice, careful attention to details, and seeking clarification when needed are key strategies in achieving successful geometry answers.
Tips and Tricks for Accurate Geometry Answers
Geometry can be a challenging subject, but with the right approach and some helpful tips and tricks, you can improve your accuracy in finding geometry answers. Whether you’re working on problems involving angles, shapes, or measurements, these strategies will help you solve them accurately and efficiently.
1. Understand the problem
Before attempting to solve a geometry problem, take the time to understand what is being asked. Read the problem carefully and identify the key given information and what you need to find. Sketching a diagram can also help you visualize the problem and identify any relevant properties or relationships.
2. Use appropriate formulas and theorems
Geometry is based on a set of formulas and theorems that help us solve problems. Make sure you have a good understanding of these formulas and theorems and know when to apply them. Using the correct formula or theorem will ensure that your answers are accurate.
3. Pay attention to units
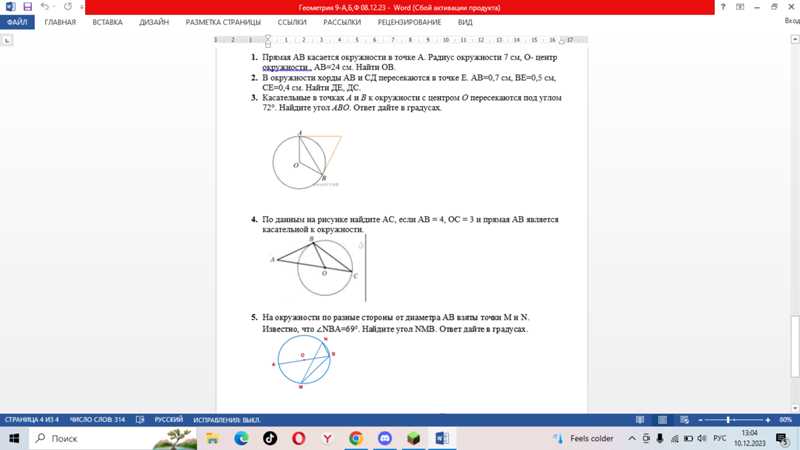
When working with measurements, make sure to pay attention to the units involved. Whether it’s centimeters, inches, or degrees, using the correct units and converting between them if necessary is crucial for accurate answers. Don’t forget to include the appropriate unit in your final answer.
4. Label your diagrams
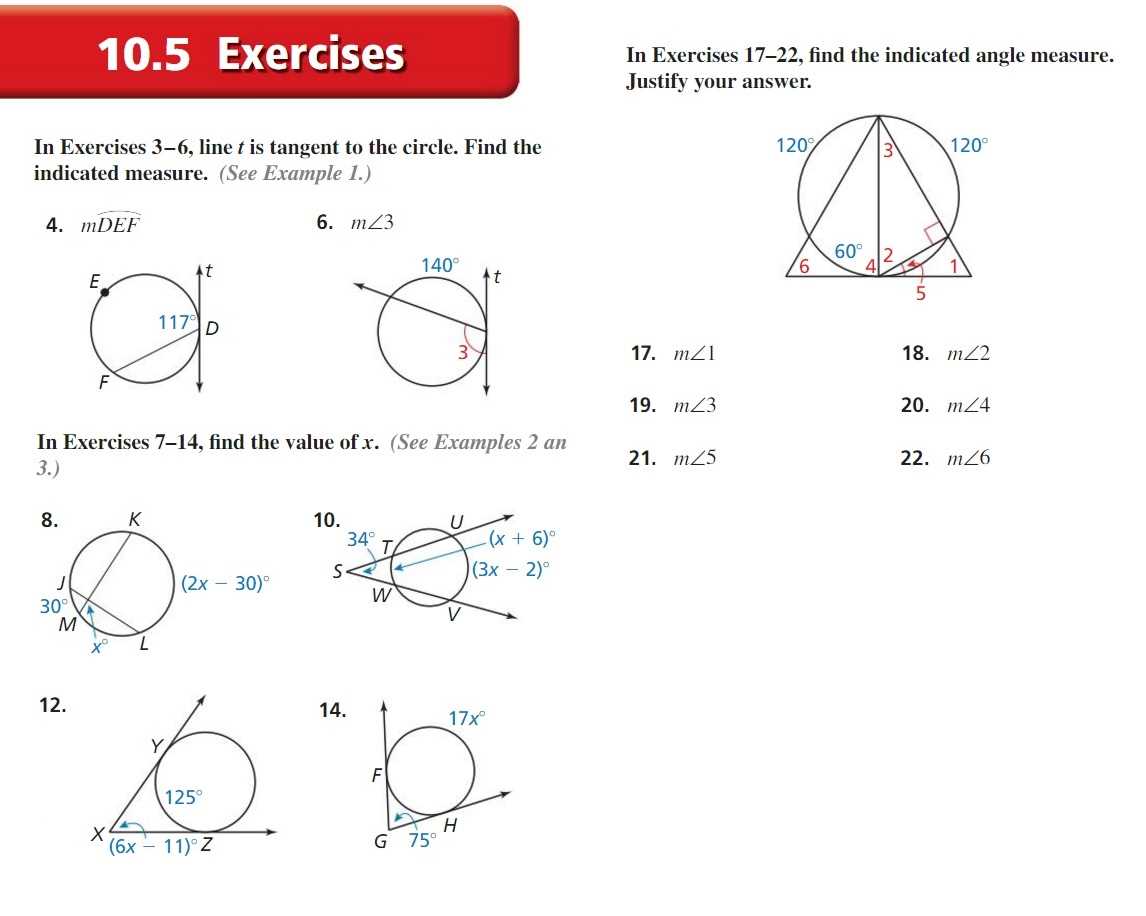
Labeling your diagrams can help you keep track of the different angles, sides, or vertices involved in a problem. By clearly labeling each part, you can avoid confusion and ensure that your calculations are accurate. It also makes it easier for others, such as teachers or classmates, to understand your work.
5. Check your work
After solving a geometry problem, take the time to check your work. This includes double-checking your calculations, making sure you haven’t made any careless mistakes, and verifying that your answer makes sense in the given context. Checking your work is an essential step in ensuring the accuracy of your geometry answers.
In conclusion
Geometry requires precision, attention to detail, and a solid understanding of the concepts. By following these tips and tricks, you can enhance your accuracy in finding geometry answers. Remember to take your time, practice regularly, and seek clarification if needed. With patience and practice, you’ll become more confident in your geometry skills and improve your ability to find accurate answers.
Q&A:
How can I improve accuracy in solving geometry problems?
You can improve accuracy in solving geometry problems by carefully reading and understanding the problem, drawing accurate diagrams, using relevant theorems and formulas, and double-checking your calculations.
What are some common mistakes to avoid when solving geometry problems?
Some common mistakes to avoid when solving geometry problems include misreading the problem, making incorrect assumptions, not labeling or measuring angles and sides accurately, and forgetting to include all necessary steps in your solution.
What should I do if I am unsure about how to approach a geometry problem?
If you are unsure about how to approach a geometry problem, start by reviewing any relevant theorems or formulas. Break the problem down into smaller parts and try to identify any patterns or relationships. Experiment with different strategies and seek help from a teacher or classmate if necessary.
How can I check if my geometry answer is correct?
You can check if your geometry answer is correct by re-reading the problem and reviewing your solution step by step. Make sure you have included all necessary calculations and that your reasoning is clear. If possible, try solving the problem using a different method or approach to see if you get the same answer.
What are some helpful tips for remembering geometry formulas and theorems?
Some helpful tips for remembering geometry formulas and theorems include creating flashcards or mnemonic devices, practicing regularly, and using the formulas and theorems in solving practice problems. It can also be helpful to understand the logic and reasoning behind the formulas and theorems, rather than just memorizing them.