
Exponential functions are an essential topic in mathematics that find extensive applications in various fields such as finance, growth models, and population analysis. These functions are characterized by a constant base raised to a variable exponent, resulting in exponential growth or decay.
In order to fully grasp the concept of exponential functions and their properties, extra practice is often necessary. This article provides an answer key for the 6-2 additional practice problems on exponential functions. By referring to this answer key, students can check their solutions and gain a better understanding of the underlying concepts.
The 6-2 additional practice problems cover a range of topics related to exponential functions, including identifying exponential growth and decay, evaluating exponential functions for specific values, and solving exponential equations. By working through these practice problems and referring to the answer key, students can reinforce their knowledge and improve their problem-solving skills in this important area of mathematics.
Overall, the 6-2 additional practice exponential functions answer key provides a valuable resource for students looking to improve their understanding and proficiency in this topic. By utilizing this answer key, students can confidently check their solutions and strengthen their grasp of exponential functions and their applications.
-2 Additional Practice Exponential Functions Answer Key
In mathematics, exponential functions play a significant role in modeling various real-world phenomena. They are especially useful in situations involving continuous growth or decay over time. The -2 Additional Practice Exponential Functions Answer Key provides students with the answers to the exercises in the Additional Practice section of the textbook, allowing them to check their work and gauge their understanding of the concepts. By using this answer key, students can identify any mistakes they may have made and learn from them, enhancing their problem-solving skills.
The answer key includes step-by-step solutions and explanations for each problem, ensuring that students grasp the underlying concepts and techniques. This comprehensive guide helps students verify their answers, gain confidence in their abilities, and reinforce their understanding of exponential functions. Through practice and review using the -2 Additional Practice Exponential Functions Answer Key, students can solidify their knowledge and improve their performance in mathematics.
By providing a comprehensive set of answers and explanations, the answer key allows students to independently assess their progress and identify areas for improvement. It serves as a valuable resource for both students and instructors, facilitating independent study and promoting self-guided learning. Whether for homework assignments, test preparation, or general reinforcement, the -2 Additional Practice Exponential Functions Answer Key is a valuable tool for students seeking to master exponential functions and their applications.
Understanding Exponential Functions

Exponential functions are mathematical expressions that involve a variable raised to a power. They are commonly used to model situations that involve growth or decay over time. The general form of an exponential function is f(x) = a * b^x, where a and b are constants and x is the independent variable. The base of the exponential function, b, is usually greater than 1 for growth functions and between 0 and 1 for decay functions.
Exponential functions have several key properties that allow us to analyze and understand their behavior. One important property is exponential growth, which occurs when the base of the function is greater than 1. In this case, as the input variable, x, increases, the output value, f(x), grows at an increasing rate. This exponential growth can result in very large values for f(x) as x approaches infinity.
Conversely, exponential decay occurs when the base of the function is between 0 and 1. In this case, as x increases, the output value f(x) decreases at a decreasing rate. Exponential decay functions model situations where the quantity being modeled diminishes over time, such as radioactive decay or the depreciation of an asset.
Exponential functions also exhibit a property called the “doubling time” or “half-life.” The doubling time is the amount of time it takes for the output value to double, while the half-life is the amount of time it takes for the output value to decrease by half. These properties are especially relevant in the context of exponential growth or decay rates.
It is important to understand exponential functions and their properties because they are widely used in various fields such as economics, finance, biology, and physics. By analyzing and manipulating exponential functions, we can make predictions, solve problems, and gain valuable insights into real-world phenomena.
Graphing Exponential Functions
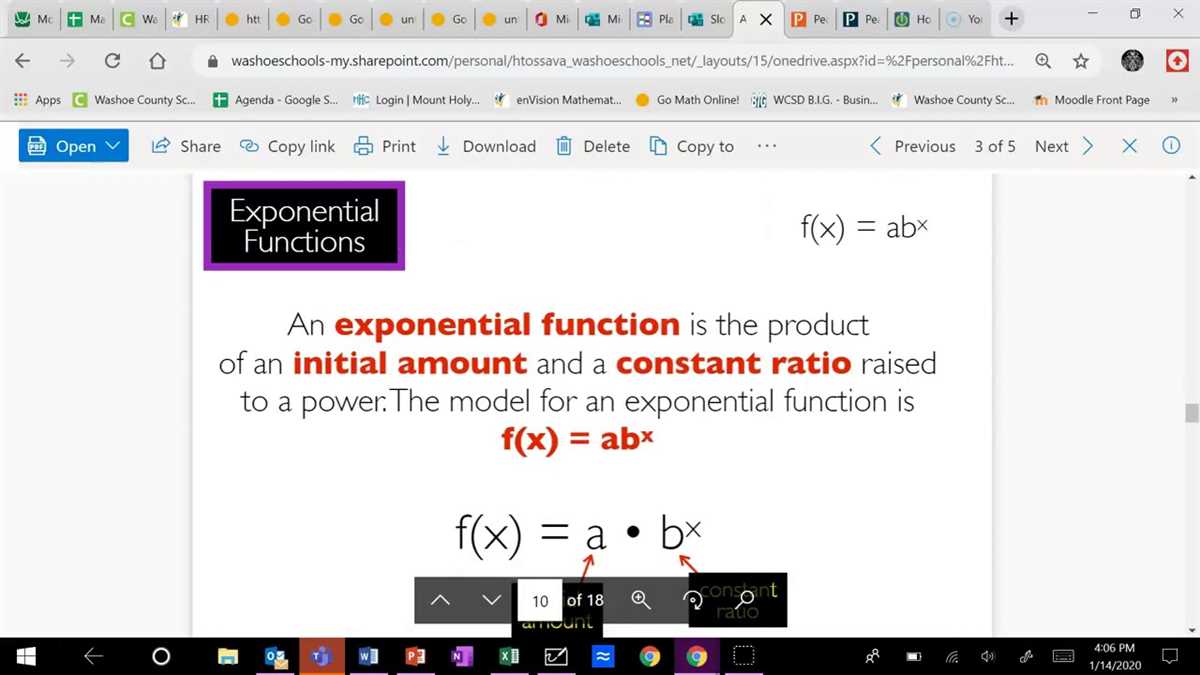
An exponential function is a mathematical function in which the variable appears in the exponent. It is of the form y = a * b^x, where a and b are constants. The variable x represents the input, and y represents the output of the function.
To graph an exponential function, we can use the method of plotting points. We choose a few values of x, plug them into the function, and calculate the corresponding y-values. These pairs of x and y values can then be plotted on a coordinate grid. With enough points, we can connect them to create the graph of the exponential function.
When graphing exponential functions, it’s important to note a few key characteristics. If the base of the exponent, b, is greater than 1, the function will be increasing as x increases. This means the graph will start at a low point and curve upwards. On the other hand, if b is between 0 and 1, the function will be decreasing as x increases. In this case, the graph will start at a high point and curve downwards.
Furthermore, the value of a determines the y-intercept of the graph. If a is positive, the graph will intercept the y-axis above zero. If a is negative, the graph will intercept the y-axis below zero.
In summary, graphing exponential functions involves choosing values of x, calculating the corresponding y-values, and plotting them on a coordinate grid. The shape and direction of the graph depend on the base of the exponent, while the y-intercept is determined by the constant a. Understanding these characteristics can help us in analyzing and interpreting exponential functions.
Solving Exponential Equations
Exponential equations involve variables in the exponent, making them more challenging to solve compared to linear or quadratic equations. However, with the proper understanding of exponent rules and techniques, it is possible to find the solutions to these equations.
One approach to solving exponential equations is by using logarithms. By taking the logarithm of both sides of the equation, we can bring the variable out of the exponent, making it easier to solve for. The choice of logarithm base depends on the specific equation, but common choices include natural logarithm (base e) and common logarithm (base 10).
Another technique for solving exponential equations is by recognizing common exponential patterns. For example, if the equation has the form (a^x = b) or (a^x = a^c), we can use logarithms to determine the value of x. Additionally, if the equation has the form (a cdot b^x = c), we can divide both sides by a to simplify the equation and then use logarithms to find the value of x.
It is important to keep in mind that exponential equations may have multiple solutions, and it is necessary to check if the obtained solutions satisfy the original equation. In cases where the equation cannot be solved exactly, numerical methods or approximation techniques may be employed to obtain an approximate solution.
- Solving exponential equations requires knowledge of exponent rules and techniques.
- One approach is to use logarithms to bring the variable out of the exponent.
- Recognizing common exponential patterns can also help in solving these equations.
- Remember to check if the obtained solutions are valid by substituting them back into the original equation.
- If an exact solution is not possible, numerical or approximation methods can be used to find an approximate solution.
Exponential Growth and Decay
Exponential growth and decay are mathematical models that describe the increase or decrease of a quantity over time. These models are often used to analyze population growth, financial investments, radioactive decay, and other natural or man-made phenomena.
In exponential growth, the quantity increases at a constant rate, with the amount of increase in each time period being proportional to the current value of the quantity. This results in a rapid growth pattern, where the quantity doubles or triples in a short period of time. The growth rate is typically represented by a positive number called the growth factor or the rate of growth.
On the other hand, exponential decay occurs when the quantity decreases at a constant rate, with the amount of decrease in each time period being proportional to the current value of the quantity. This leads to a gradual decline in the quantity over time. The decay rate is represented by a negative number called the decay factor or the rate of decay.
This exponential growth and decay can be described by a mathematical function called an exponential function. The general form of an exponential function is given by:
y = a * b^x
- y represents the final amount or the value of the quantity after a certain period of time.
- a is the initial amount or the starting value of the quantity.
- b is the growth or decay factor, which determines the rate of change.
- x represents the time period or the number of intervals that have passed.
By understanding and analyzing exponential growth and decay, we can make predictions, solve real-world problems, and make informed decisions in various fields, such as finance, biology, and physics.
Applications of Exponential Functions
Exponential functions are widely used in various fields to model and describe phenomena that grow or decay exponentially over time. These functions are characterized by a constant base raised to a variable exponent, resulting in a graph that exhibits rapid growth or decay.
Financial Growth: Exponential functions find application in the world of finance, where they are used to model compound interest and exponential growth of investments. For example, when calculating the future value of an investment with a fixed interest rate, an exponential function can be used to determine how the value will grow over time. This allows investors to make informed decisions and plan for the future.
Population Growth: Exponential functions play a crucial role in demography, where they are used to study population growth and predict future populations. By considering factors such as birth rates, death rates, and immigration, demographers can construct exponential models to estimate how populations will change over time. This information is valuable for urban planning, resource allocation, and policy-making.
Radioactive Decay: In the field of nuclear physics, exponential functions are used to model the decay of radioactive substances. The rate at which radioactive isotopes decay is proportional to the amount of the substance present at any given time. By using exponential functions, scientists can determine the half-life of a radioactive material and understand its behavior over time. This knowledge is important for applications such as radiocarbon dating and radiation therapy.
Epidemiology: Exponential functions are also employed in epidemiology to study the spread of diseases and predict future outbreaks. By considering factors such as transmission rates, recovery rates, and vaccination rates, epidemiologists can create mathematical models that simulate the progression of infectious diseases. These models help inform public health policies, guide interventions, and estimate the impact of various control measures.
Technology Growth: Exponential functions are closely associated with technological advancements, particularly in the realm of computing and information technology. Moore’s Law, for example, states that the number of transistors on a microchip doubles approximately every two years. This exponential growth has fueled the development of increasingly powerful computers and other technological innovations. Exponential functions allow us to understand and predict the growth of technology, driving innovation forward.
Overall, exponential functions provide valuable tools for analyzing and predicting various phenomena in the realms of finance, demography, physics, epidemiology, and technology. Their ability to capture exponential growth or decay enables us to make informed decisions, plan for the future, and understand the complex dynamics of these systems.
Common Mistakes and How to Avoid Them
When working with exponential functions, it is important to be aware of common mistakes that students often make. By understanding these mistakes and learning how to avoid them, you can improve your accuracy and confidence in solving exponential function problems. Here are some common mistakes and tips on how to avoid them:
1. Forgetting to simplify the base
One common mistake is forgetting to simplify the base of the exponential function. It is important to simplify the base before performing any calculations. By simplifying the base, you can avoid errors and make the calculations easier.
Tip: Always simplify the base of the exponential function if possible. Look for any common factors or simplifiable expressions and simplify them to make the calculations more manageable.
2. Misinterpreting negative exponents
Another mistake is misinterpreting negative exponents. Negative exponents indicate taking the reciprocal of the base raised to the positive exponent. Misinterpreting negative exponents can lead to incorrect solutions.
Tip: When encountering a negative exponent, remember to take the reciprocal of the base raised to the positive exponent. This will help you avoid errors and obtain the correct solution.
3. Not using parentheses

Not using parentheses can also lead to mistakes when working with exponential functions. This is especially true when dealing with complex expressions or multiple operations.
Tip: Always use parentheses to clearly indicate the correct order of operations. This will help you avoid confusion and ensure accurate calculations.
4. Rounding errors
Rounding errors can occur when working with decimal approximations of exponential values. These errors can accumulate and lead to significant differences in the final result.
Tip: To minimize rounding errors, carry out calculations with as many decimal places as possible before rounding the final answer. This will help maintain accuracy and reduce the impact of rounding errors.
By being aware of these common mistakes and following the provided tips, you can improve your understanding and mastery of exponential functions. Practice regularly and seek clarification from your teacher or peers if you are unsure about any concepts or steps. With time and effort, you will become more proficient in solving exponential function problems and achieve success in your math studies.