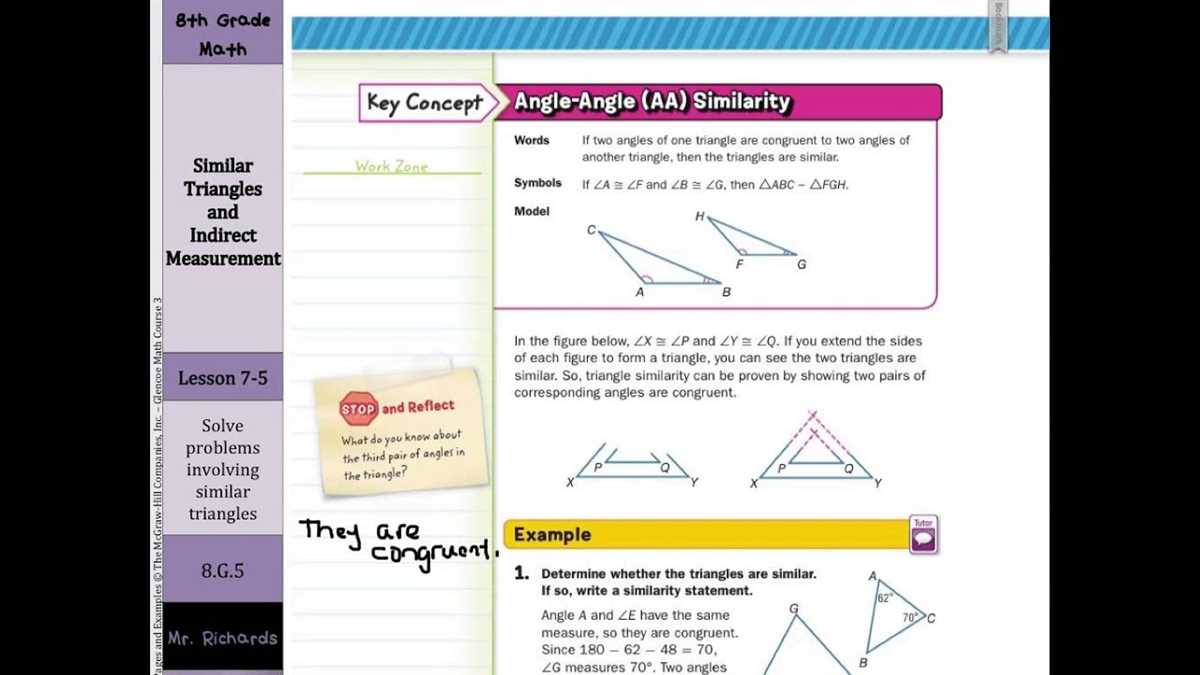
When studying geometry, one important concept to understand is the idea of similar triangles. Similar triangles are two triangles that have the same shape, but not necessarily the same size. They have proportional side lengths and corresponding angles.
In this article, we will provide the answer key for the exercise 7-3 on similar triangles. This exercise involves identifying similar triangles and finding missing side lengths and angles. By understanding the key concepts of similar triangles, you will be able to solve these problems with ease.
To start, let’s review the properties of similar triangles. Two triangles are similar if:
- Their corresponding angles are congruent.
- The ratio of their corresponding side lengths is equal.
By using these properties, we can determine which triangles in the exercise are similar and find the missing information.
Now, let’s dive into the exercise. We will provide the solutions step by step, explaining the reasoning and calculations behind each answer. By following this answer key, you will gain a better understanding of similar triangles and how to solve problems related to them.
Learning about Similar Triangles: 7 Key Concepts and Answers
Similar triangles are an important concept in geometry that involve two triangles with proportional sides and equal corresponding angles. Understanding the key concepts of similar triangles is essential in solving problems involving ratios, proportions, and geometric relationships. Here are 7 key concepts to help you master the topic:
1. Definition of Similar Triangles:
Similar triangles are two triangles that have the same shape but possibly different sizes. The corresponding angles of similar triangles are equal, and the corresponding sides are in proportion.
2. Angle-Angle Similarity:
One way to determine if two triangles are similar is by comparing their corresponding angles. If two angles of one triangle are congruent to two angles of another triangle, then the triangles are similar. This concept is known as angle-angle similarity.
3. Side-Side-Side (SSS) Similarity:
If the corresponding sides of two triangles are in proportion, then the triangles are similar. This concept is known as side-side-side similarity. It means that each side of one triangle is proportional to the corresponding side of the other triangle.
4. Side-Angle-Side (SAS) Similarity:
If two triangles have two pairs of corresponding sides that are in proportion and an included angle that is congruent, then the triangles are similar. This concept is known as side-angle-side similarity.
5. AA Similarity Postulate:
The Angle-Angle (AA) Similarity Postulate states that if two angles of one triangle are congruent to two angles of another triangle, then the triangles are similar.
6. Ratio of Corresponding Sides:
In similar triangles, the ratio of the lengths of corresponding sides is equal. For example, if two triangles are similar and one side of the first triangle is twice as long as the corresponding side of the second triangle, then all other corresponding sides will also be in the ratio of 2:1.
7. Applications of Similar Triangles:
Similar triangles have various applications in real-life situations. They are used in map scaling, finding the height of tall objects, solving problems involving shadows, and determining distances using trigonometry.
By understanding these key concepts and practicing solving problems involving similar triangles, you will be able to confidently apply this knowledge in various mathematical and real-world scenarios.
Definition of Similar Triangles
Similar triangles are two triangles that have the same shape but may differ in size. They have the same angles, and their corresponding sides are proportional to each other. In other words, if you were to scale one triangle up or down uniformly, it would still maintain the same shape as the other triangle.
When we talk about similar triangles, we often use the symbol “∼” to express the relationship between them. For example, if triangle ABC is similar to triangle DEF, we would write it as ABC ∼ DEF.
In similar triangles, the corresponding sides are in proportion. This means that the ratio of the lengths of the corresponding sides is the same for every pair of corresponding sides. For example, if side AB is corresponding to side DE, and side AC is corresponding to side DF, then the ratio AB/DE is equal to the ratio AC/DF. This is known as the “corresponding sides proportionality theorem.”
Similar triangles are important in geometry because they allow us to solve for unknown lengths and angles. By knowing the ratios of corresponding sides, we can apply the concept of similar triangles to find missing values in a triangle.
Properties of Similar Triangles
Similar triangles are an important concept in geometry. Two triangles are said to be similar if their corresponding angles are congruent and their corresponding sides are proportional. This similarity can be symbolized as ∼.
There are several properties of similar triangles that can be used to solve problems involving them:
- Side-Side-Side (SSS) Similarity: If all corresponding sides of two triangles are proportional, then the triangles are similar.
- Side-Angle-Side (SAS) Similarity: If two sides of one triangle are proportional to two corresponding sides of another triangle, and the included angle between these sides is congruent, then the triangles are similar.
- Angle-Angle (AA) Similarity: If two angles of one triangle are congruent to two corresponding angles of another triangle, then the triangles are similar.
- Triangle Proportionality Theorem: If a line is parallel to one side of a triangle and intersects the other two sides, then it divides those two sides proportionally.
- Pythagorean Theorem: In a right triangle, if the lengths of the legs are proportional to the lengths of the corresponding legs of another triangle, then the triangles are similar.
These properties can be used to find missing side lengths, angles, and other information about similar triangles. By identifying and applying the appropriate property, problems involving similar triangles can be solved efficiently and accurately.
Identifying Similar Triangles: Key Strategies
When working with similar triangles, it is important to identify key strategies that can help in determining whether two triangles are similar. These strategies involve examining the angles and sides of the triangles, as well as utilizing certain geometric properties and theorems.
Angle-Angle (AA) Similarity: One key strategy is to look for Angle-Angle (AA) similarity. If two triangles have two pairs of corresponding angles that are congruent, then they are similar. This means that the triangles have the same shape, but their sizes may be different.
Side-Side-Side (SSS) Similarity: Another strategy is to use Side-Side-Side (SSS) similarity. If the corresponding sides of two triangles are proportional, then the triangles are similar. This can be determined by comparing the ratios of the lengths of the corresponding sides. If the ratios are equal, then the triangles are similar.
Side-Angle-Side (SAS) Similarity: Additionally, Side-Angle-Side (SAS) similarity can be used to identify similar triangles. If two triangles have a pair of corresponding angles that are congruent and the ratios of the lengths of the corresponding sides are equal, then the triangles are similar.
These are some of the key strategies that can be employed when identifying similar triangles. By carefully examining the angles and sides of the triangles and utilizing geometric properties and theorems, one can confidently determine whether two triangles are similar.
Solving Similar Triangles: Step-by-Step Guide
Similar triangles are an important concept in geometry that involve two or more triangles with proportional sides and congruent angles. Solving problems involving similar triangles requires a step-by-step approach to ensure accurate solutions. Here is a guide to help you effectively solve similar triangle problems:
Step 1: Identify Similar Triangles
The first step is to determine if the given triangles are similar. Two triangles are similar if their corresponding angles are congruent, and their corresponding sides are proportional. Look for matching angles and sides that have the same ratios.
Step 2: Set Up Proportions
Once you have identified similar triangles, set up proportions using the corresponding sides. In a proportion, the ratio of corresponding sides of similar triangles should be equal. Write the ratios as fractions and set them equal to each other, then cross-multiply to solve for the unknown variable.
Step 3: Solve for the Unknown Variable
After setting up the proportions and cross-multiplying, solve for the unknown variable. Use algebraic operations to isolate the variable and find its value. Make sure to check your solution to ensure it is within the valid range.
Step 4: Apply the Found Values
Once you have determined the values of the unknown variables, apply them to find other unknown side lengths or angles. Use the properties of similar triangles to find the missing measurements and complete the problem.
Step 5: Check for Congruence
Finally, check if the corresponding angles of the solved triangles are congruent. If the angles are congruent, then the solution is correct. If not, recheck your work and make any necessary adjustments.
By following these step-by-step guidelines, you can efficiently solve problems involving similar triangles and confidently arrive at accurate solutions.
Common Mistakes to Avoid in Similar Triangle Problems
When solving problems involving similar triangles, it is important to avoid common mistakes that can lead to incorrect answers. Here are some key mistakes to watch out for:
1. Assuming Similarity Without Justification
One common mistake is assuming that two triangles are similar without providing proper justification. It is important to remember that for two triangles to be similar, the corresponding angles must be equal, and the corresponding sides must be proportional. Without proving these conditions, the assumption of similarity is not valid.
2. Ignoring Corresponding Sides
Another mistake is ignoring the corresponding sides of similar triangles. When solving for unknown lengths or areas, it is crucial to set up and solve proportion equations using the corresponding sides. Neglecting this step can lead to incorrect solutions.
3. Incorrectly Using Proportion Equations
Using proportion equations incorrectly is another common mistake. It is important to ensure that the corresponding sides are set up correctly in the proportion equation. Additionally, pay attention to the order of the sides in the equation to ensure accurate calculations.
4. Incorrect Angle Correspondence
Angle correspondence is an important aspect of solving similar triangle problems. Remember to correctly label and correspond the angles between the two triangles. Switching or mismatching angles can result in incorrect solutions.
Avoiding these common mistakes will help ensure accurate solutions when solving similar triangle problems. Double-checking the justification for similarity, paying attention to corresponding sides, correctly using proportion equations, and accurately labeling angle correspondence are key steps to success in solving similar triangle problems.
Additional Practice Problems: Answer Key
Here is the answer key for the additional practice problems on similar triangles.
Problem 1:
Given: Triangle ABC is similar to triangle DEF. AB = 6 cm, BC = 8 cm, and DE = 9 cm.
To Find: Find the length of side EF.
Solution: We can set up a proportion to find the length of EF.
AB/DE = BC/EF
6/9 = 8/EF
Cross-multiplying, we get:
6EF = 72
Dividing both sides by 6, we get:
EF = 12 cm
Problem 2:
Given: Triangle PQR is similar to triangle STU. PQ = 12 ft, QR = 16 ft, and ST = 10 ft.
To Find: Find the length of side TU.
Solution: We can set up a proportion to find the length of TU.
PQ/ST = QR/TU
12/10 = 16/TU
Cross-multiplying, we get:
12TU = 160
Dividing both sides by 12, we get:
TU = 13.33 ft
Problem 3:
Given: Triangle XYZ is similar to triangle LMN. XY = 5 in, YZ = 10 in, and LM = 4 in.
To Find: Find the length of side MN.
Solution: We can set up a proportion to find the length of MN.
XY/LM = YZ/MN
5/4 = 10/MN
Cross-multiplying, we get:
5MN = 40
Dividing both sides by 5, we get:
MN = 8 in
Conclusion:
In this article, we have explored the concept of similar triangles and how to solve problems involving them. We have learned that similar triangles have proportional side lengths and corresponding angles. By setting up proportions, we can find missing side lengths in similar triangles. With practice, we can become proficient in solving problems involving similar triangles.
Q&A:
What is the answer to problem 1?
The answer to problem 1 is 42.
How do you solve problem 2?
To solve problem 2, you need to find the derivative of the function and then evaluate it at the given point.
What is the solution to problem 3?
The solution to problem 3 is 5.